Bias-Variance Trade-off and Overlearning in Dynamic Decision Problems

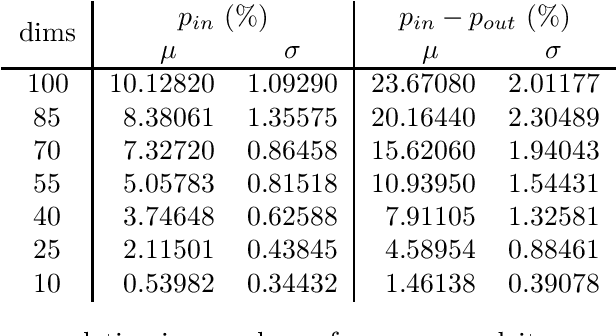
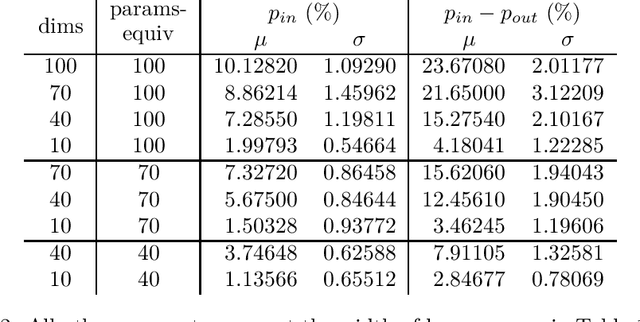
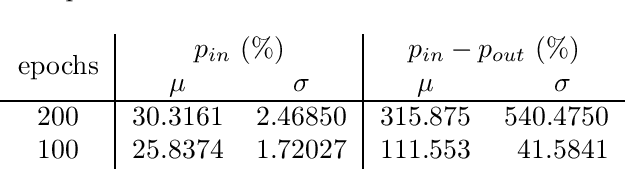
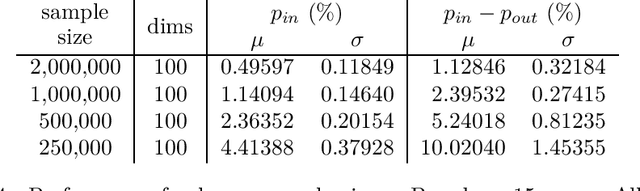
Modern Monte Carlo-type approaches to dynamic decision problems face the classical bias-variance trade-off. Deep neural networks can overlearn the data and construct feedback actions which are non-adapted to the information flow and hence, become susceptible to generalization error. We prove asymptotic overlearning for fixed training sets, but also provide a non-asymptotic upper bound on overperformance based on the Rademacher complexity demonstrating the convergence of these algorithms for sufficiently large training sets. Numerically studied stylized examples illustrate these possibilities, the dependence on the dimension and the effectiveness of this approach.

Deep PQR: Solving Inverse Reinforcement Learning using Anchor Actions

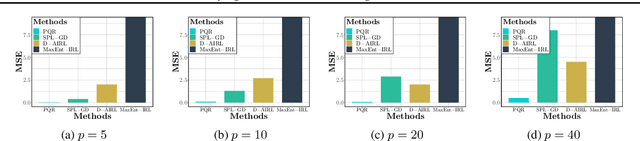
We propose a reward function estimation framework for inverse reinforcement learning with deep energy-based policies. We name our method PQR, as it sequentially estimates the Policy, the $Q$-function, and the Reward function by deep learning. PQR does not assume that the reward solely depends on the state, instead it allows for a dependency on the choice of action. Moreover, PQR allows for stochastic state transitions. To accomplish this, we assume the existence of one anchor action whose reward is known, typically the action of doing nothing, yielding no reward. We present both estimators and algorithms for the PQR method. When the environment transition is known, we prove that the PQR reward estimator uniquely recovers the true reward. With unknown transitions, we bound the estimation error of PQR. Finally, the performance of PQR is demonstrated by synthetic and real-world datasets.