Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
H. Mete Soner
Bias-Variance Trade-off and Overlearning in Dynamic Decision Problems
Nov 18, 2020Figures and Tables: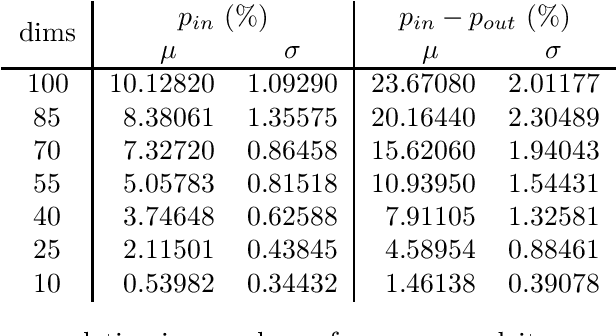
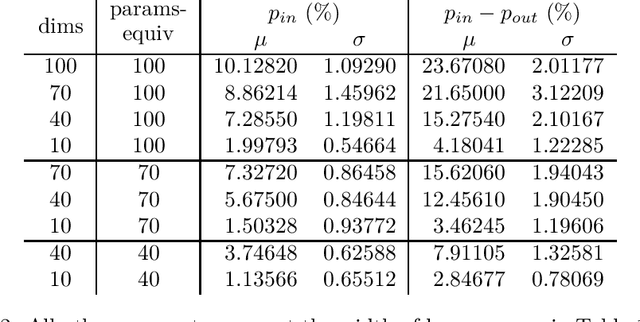
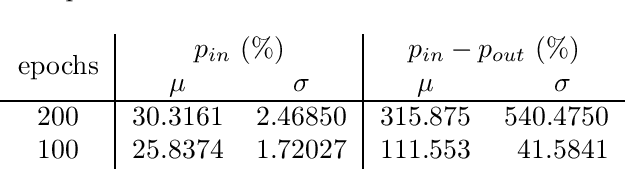
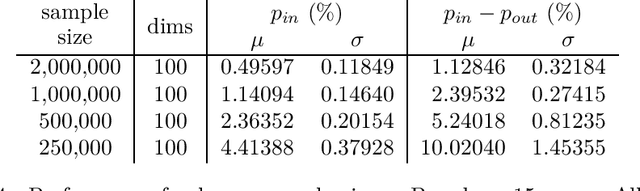


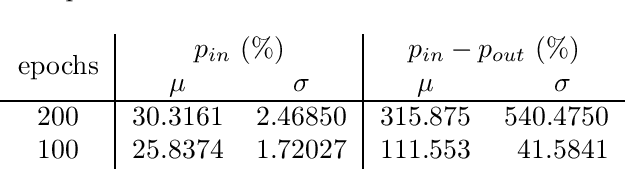

Abstract:Modern Monte Carlo-type approaches to dynamic decision problems face the classical bias-variance trade-off. Deep neural networks can overlearn the data and construct feedback actions which are non-adapted to the information flow and hence, become susceptible to generalization error. We prove asymptotic overlearning for fixed training sets, but also provide a non-asymptotic upper bound on overperformance based on the Rademacher complexity demonstrating the convergence of these algorithms for sufficiently large training sets. Numerically studied stylized examples illustrate these possibilities, the dependence on the dimension and the effectiveness of this approach.
* 25 pages, 4 Tables
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge