Influencing Bandits: Arm Selection for Preference Shaping

We consider a non stationary multi-armed bandit in which the population preferences are positively and negatively reinforced by the observed rewards. The objective of the algorithm is to shape the population preferences to maximize the fraction of the population favouring a predetermined arm. For the case of binary opinions, two types of opinion dynamics are considered -- decreasing elasticity (modeled as a Polya urn with increasing number of balls) and constant elasticity (using the voter model). For the first case, we describe an Explore-then-commit policy and a Thompson sampling policy and analyse the regret for each of these policies. We then show that these algorithms and their analyses carry over to the constant elasticity case. We also describe a Thompson sampling based algorithm for the case when more than two types of opinions are present. Finally, we discuss the case where presence of multiple recommendation systems gives rise to a trade-off between their popularity and opinion shaping objectives.

Learning Recommendations While Influencing Interests

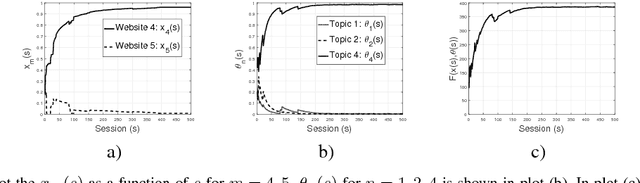
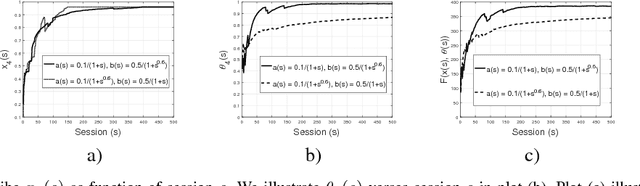
Personalized recommendation systems (RS) are extensively used in many services. Many of these are based on learning algorithms where the RS uses the recommendation history and the user response to learn an optimal strategy. Further, these algorithms are based on the assumption that the user interests are rigid. Specifically, they do not account for the effect of learning strategy on the evolution of the user interests. In this paper we develop influence models for a learning algorithm that is used to optimally recommend websites to web users. We adapt the model of \cite{Ioannidis10} to include an item-dependent reward to the RS from the suggestions that are accepted by the user. For this we first develop a static optimisation scheme when all the parameters are known. Next we develop a stochastic approximation based learning scheme for the RS to learn the optimal strategy when the user profiles are not known. Finally, we describe several user-influence models for the learning algorithm and analyze their effect on the steady user interests and on the steady state optimal strategy as compared to that when the users are not influenced.

Optimal Recommendation to Users that React: Online Learning for a Class of POMDPs

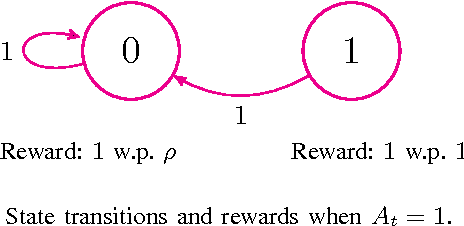
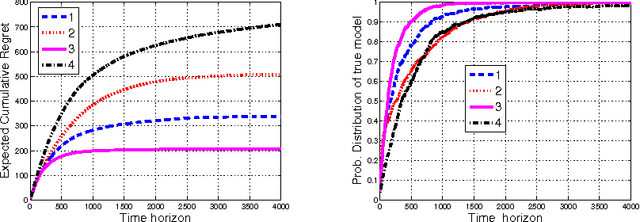
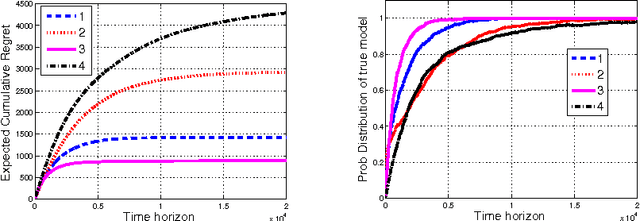
We describe and study a model for an Automated Online Recommendation System (AORS) in which a user's preferences can be time-dependent and can also depend on the history of past recommendations and play-outs. The three key features of the model that makes it more realistic compared to existing models for recommendation systems are (1) user preference is inherently latent, (2) current recommendations can affect future preferences, and (3) it allows for the development of learning algorithms with provable performance guarantees. The problem is cast as an average-cost restless multi-armed bandit for a given user, with an independent partially observable Markov decision process (POMDP) for each item of content. We analyze the POMDP for a single arm, describe its structural properties, and characterize its optimal policy. We then develop a Thompson sampling-based online reinforcement learning algorithm to learn the parameters of the model and optimize utility from the binary responses of the users to continuous recommendations. We then analyze the performance of the learning algorithm and characterize the regret. Illustrative numerical results and directions for extension to the restless hidden Markov multi-armed bandit problem are also presented.