Faster Q-Learning Algorithms for Restless Bandits

We study the Whittle index learning algorithm for restless multi-armed bandits (RMAB). We first present Q-learning algorithm and its variants -- speedy Q-learning (SQL), generalized speedy Q-learning (GSQL) and phase Q-learning (PhaseQL). We also discuss exploration policies -- $\epsilon$-greedy and Upper confidence bound (UCB). We extend the study of Q-learning and its variants with UCB policy. We illustrate using numerical example that Q-learning with UCB exploration policy has faster convergence and PhaseQL with UCB have fastest convergence rate. We next extend the study of Q-learning variants for index learning to RMAB. The algorithm of index learning is two-timescale variant of stochastic approximation, on slower timescale we update index learning scheme and on faster timescale we update Q-learning assuming fixed index value. We study constant stepsizes two timescale stochastic approximation algorithm. We describe the performance of our algorithms using numerical example. It illustrate that index learning with Q learning with UCB has faster convergence that $\epsilon$ greedy. Further, PhaseQL (with UCB and $\epsilon$ greedy) has the best convergence than other Q-learning algorithms.

Whittle Index Learning Algorithms for Restless Bandits with Constant Stepsizes

We study the Whittle index learning algorithm for restless multi-armed bandits. We consider index learning algorithm with Q-learning. We first present Q-learning algorithm with exploration policies -- epsilon-greedy, softmax, epsilon-softmax with constant stepsizes. We extend the study of Q-learning to index learning for single-armed restless bandit. The algorithm of index learning is two-timescale variant of stochastic approximation, on slower timescale we update index learning scheme and on faster timescale we update Q-learning assuming fixed index value. In Q-learning updates are in asynchronous manner. We study constant stepsizes two timescale stochastic approximation algorithm. We provide analysis of two-timescale stochastic approximation for index learning with constant stepsizes. Further, we present study on index learning with deep Q-network (DQN) learning and linear function approximation with state-aggregation method. We describe the performance of our algorithms using numerical examples. We have shown that index learning with Q learning, DQN and function approximations learns the Whittle index.

Indexability of Finite State Restless Multi-Armed Bandit and Rollout Policy

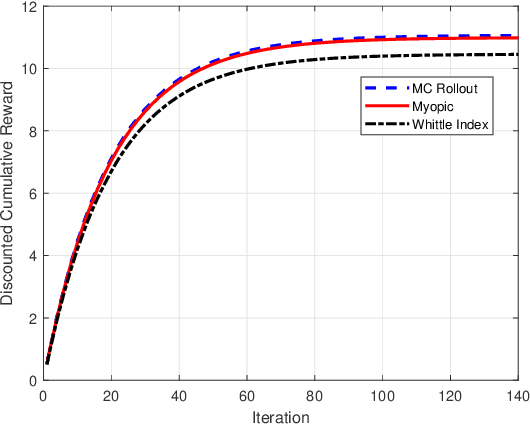
We consider finite state restless multi-armed bandit problem. The decision maker can act on M bandits out of N bandits in each time step. The play of arm (active arm) yields state dependent rewards based on action and when the arm is not played, it also provides rewards based on the state and action. The objective of the decision maker is to maximize the infinite horizon discounted reward. The classical approach to restless bandits is Whittle index policy. In such policy, the M arms with highest indices are played at each time step. Here, one decouples the restless bandits problem by analyzing relaxed constrained restless bandits problem. Then by Lagrangian relaxation problem, one decouples restless bandits problem into N single-armed restless bandit problems. We analyze the single-armed restless bandit. In order to study the Whittle index policy, we show structural results on the single armed bandit model. We define indexability and show indexability in special cases. We propose an alternative approach to verify the indexable criteria for a single armed bandit model using value iteration algorithm. We demonstrate the performance of our algorithm with different examples. We provide insight on condition of indexability of restless bandits using different structural assumptions on transition probability and reward matrices. We also study online rollout policy and discuss the computation complexity of algorithm and compare that with complexity of index computation. Numerical examples illustrate that index policy and rollout policy performs better than myopic policy.

Indexability and Rollout Policy for Multi-State Partially Observable Restless Bandits

Restless multi-armed bandits with partially observable states has applications in communication systems, age of information and recommendation systems. In this paper, we study multi-state partially observable restless bandit models. We consider three different models based on information observable to decision maker -- 1) no information is observable from actions of a bandit 2) perfect information from bandit is observable only for one action on bandit, there is a fixed restart state, i.e., transition occurs from all other states to that state 3) perfect state information is available to decision maker for both actions on a bandit and there are two restart state for two actions. We develop the structural properties. We also show a threshold type policy and indexability for model 2 and 3. We present Monte Carlo (MC) rollout policy. We use it for whittle index computation in case of model 2. We obtain the concentration bound on value function in terms of horizon length and number of trajectories for MC rollout policy. We derive explicit index formula for model 3. We finally describe Monte Carlo rollout policy for model 1 when it is difficult to show indexability. We demonstrate the numerical examples using myopic policy, Monte Carlo rollout policy and Whittle index policy. We observe that Monte Carlo rollout policy is good competitive policy to myopic.

Monte Carlo Rollout Policy for Recommendation Systems with Dynamic User Behavior

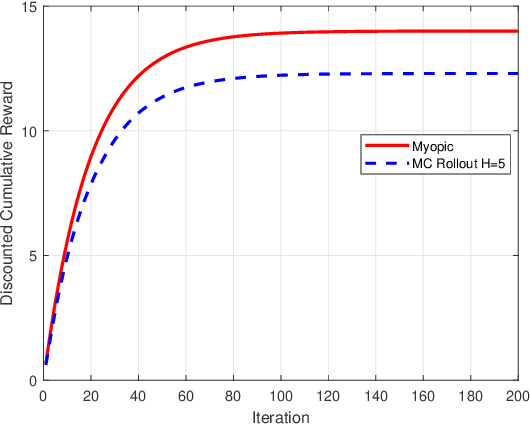
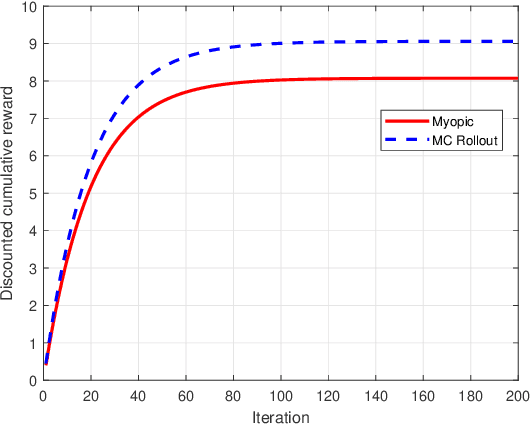
We model online recommendation systems using the hidden Markov multi-state restless multi-armed bandit problem. To solve this we present Monte Carlo rollout policy. We illustrate numerically that Monte Carlo rollout policy performs better than myopic policy for arbitrary transition dynamics with no specific structure. But, when some structure is imposed on the transition dynamics, myopic policy performs better than Monte Carlo rollout policy.

Simulation Based Algorithms for Markov Decision Processes and Multi-Action Restless Bandits

We consider multi-dimensional Markov decision processes and formulate a long term discounted reward optimization problem. Two simulation based algorithms---Monte Carlo rollout policy and parallel rollout policy are studied, and various properties for these policies are discussed. We next consider a restless multi-armed bandit (RMAB) with multi-dimensional state space and multi-actions bandit model. A standard RMAB consists of two actions for each arms whereas in multi-actions RMAB, there are more that two actions for each arms. A popular approach for RMAB is Whittle index based heuristic policy. Indexability is an important requirement to use index based policy. Based on this, an RMAB is classified into indexable or non-indexable bandits. Our interest is in the study of Monte-Carlo rollout policy for both indexable and non-indexable restless bandits. We first analyze a standard indexable RMAB (two-action model) and discuss an index based policy approach. We present approximate index computation algorithm using Monte-Carlo rollout policy. This algorithm's convergence is shown using two-timescale stochastic approximation scheme. Later, we analyze multi-actions indexable RMAB, and discuss the index based policy approach. We also study non-indexable RMAB for both standard and multi-actions bandits using Monte-Carlo rollout policy.

Sequential Decision Making under Uncertainty with Dynamic Resource Constraints

This paper studies a class of constrained restless multi-armed bandits. The constraints are in the form of time varying availability of arms. This variation can be either stochastic or semi-deterministic. A fixed number of arms can be chosen to be played in each decision interval. The play of each arm yields a state dependent reward. The current states of arms are partially observable through binary feedback signals from arms that are played. The current availability of arms is fully observable. The objective is to maximize long term cumulative reward. The uncertainty about future availability of arms along with partial state information makes this objective challenging. This optimization problem is analyzed using Whittle's index policy. To this end, a constrained restless single-armed bandit is studied. It is shown to admit a threshold-type optimal policy, and is also indexable. An algorithm to compute Whittle's index is presented. Further, upper bounds on the value function are derived in order to estimate the degree of sub-optimality of various solutions. The simulation study compares the performance of Whittle's index, modified Whittle's index and myopic policies.

Learning Recommendations While Influencing Interests

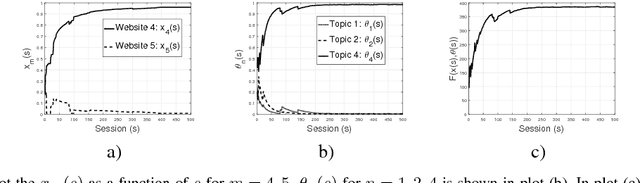
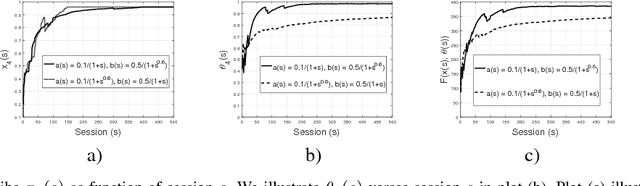
Personalized recommendation systems (RS) are extensively used in many services. Many of these are based on learning algorithms where the RS uses the recommendation history and the user response to learn an optimal strategy. Further, these algorithms are based on the assumption that the user interests are rigid. Specifically, they do not account for the effect of learning strategy on the evolution of the user interests. In this paper we develop influence models for a learning algorithm that is used to optimally recommend websites to web users. We adapt the model of \cite{Ioannidis10} to include an item-dependent reward to the RS from the suggestions that are accepted by the user. For this we first develop a static optimisation scheme when all the parameters are known. Next we develop a stochastic approximation based learning scheme for the RS to learn the optimal strategy when the user profiles are not known. Finally, we describe several user-influence models for the learning algorithm and analyze their effect on the steady user interests and on the steady state optimal strategy as compared to that when the users are not influenced.

Optimal Recommendation to Users that React: Online Learning for a Class of POMDPs

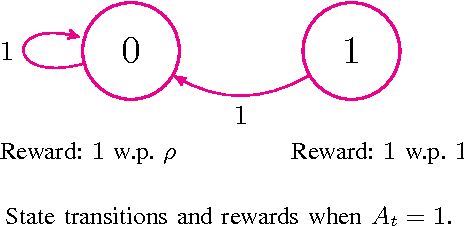
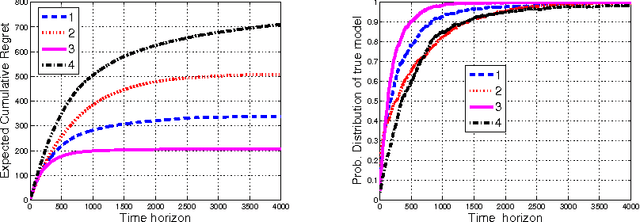
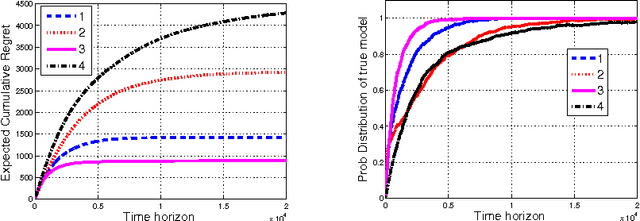
We describe and study a model for an Automated Online Recommendation System (AORS) in which a user's preferences can be time-dependent and can also depend on the history of past recommendations and play-outs. The three key features of the model that makes it more realistic compared to existing models for recommendation systems are (1) user preference is inherently latent, (2) current recommendations can affect future preferences, and (3) it allows for the development of learning algorithms with provable performance guarantees. The problem is cast as an average-cost restless multi-armed bandit for a given user, with an independent partially observable Markov decision process (POMDP) for each item of content. We analyze the POMDP for a single arm, describe its structural properties, and characterize its optimal policy. We then develop a Thompson sampling-based online reinforcement learning algorithm to learn the parameters of the model and optimize utility from the binary responses of the users to continuous recommendations. We then analyze the performance of the learning algorithm and characterize the regret. Illustrative numerical results and directions for extension to the restless hidden Markov multi-armed bandit problem are also presented.