Optimal Recommendation to Users that React: Online Learning for a Class of POMDPs
Paper and Code
Mar 30, 2016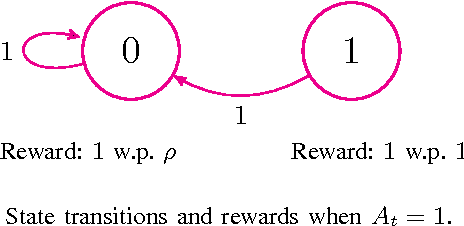
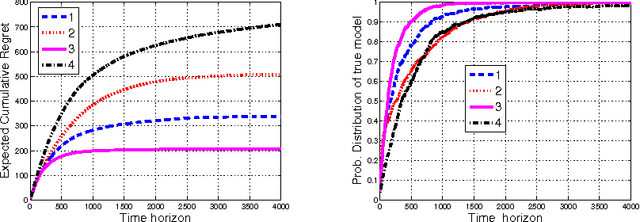
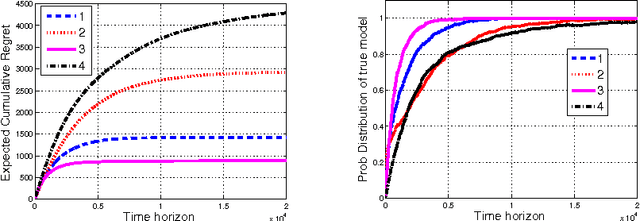
We describe and study a model for an Automated Online Recommendation System (AORS) in which a user's preferences can be time-dependent and can also depend on the history of past recommendations and play-outs. The three key features of the model that makes it more realistic compared to existing models for recommendation systems are (1) user preference is inherently latent, (2) current recommendations can affect future preferences, and (3) it allows for the development of learning algorithms with provable performance guarantees. The problem is cast as an average-cost restless multi-armed bandit for a given user, with an independent partially observable Markov decision process (POMDP) for each item of content. We analyze the POMDP for a single arm, describe its structural properties, and characterize its optimal policy. We then develop a Thompson sampling-based online reinforcement learning algorithm to learn the parameters of the model and optimize utility from the binary responses of the users to continuous recommendations. We then analyze the performance of the learning algorithm and characterize the regret. Illustrative numerical results and directions for extension to the restless hidden Markov multi-armed bandit problem are also presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge