Distributed Bandit Learning: Near-Optimal Regret with Efficient Communication
Paper and Code
May 29, 2019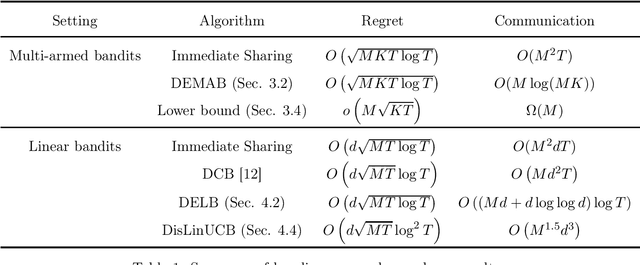
We study the problem of regret minimization for distributed bandits learning, in which $M$ agents work collaboratively to minimize their total regret under the coordination of a central server. Our goal is to design communication protocols with near-optimal regret and little communication cost, which is measured by the total amount of transmitted data. For distributed multi-armed bandits, we propose a protocol with near-optimal regret and only $O(M\log(MK))$ communication cost, where $K$ is the number of arms. The communication cost is independent of the time horizon $T$, has only logarithmic dependence on the number of arms, and matches the lower bound except for a logarithmic factor. For distributed $d$-dimensional linear bandits, we propose a protocol that achieves near-optimal regret and has communication cost of order $\tilde{O}(Md)$, which has only logarithmic dependence on $T$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge