Multi-scale Online Learning and its Applications to Online Auctions
Paper and Code
Sep 11, 2018
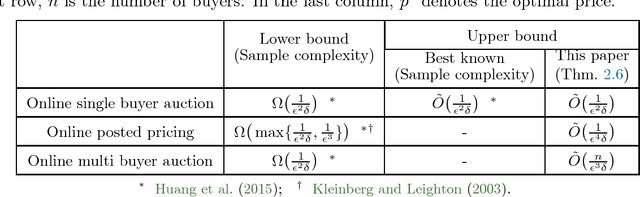

We consider revenue maximization in online auction/pricing problems. A seller sells an identical item in each period to a new buyer, or a new set of buyers. For the online posted pricing problem, we show regret bounds that scale with the best fixed price, rather than the range of the values. We also show regret bounds that are almost scale free, and match the offline sample complexity, when comparing to a benchmark that requires a lower bound on the market share. These results are obtained by generalizing the classical learning from experts and multi-armed bandit problems to their multi-scale versions. In this version, the reward of each action is in a different range, and the regret w.r.t. a given action scales with its own range, rather than the maximum range.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge