Marwa El Halabi
Discrete and Continuous Difference of Submodular Minimization
Jun 09, 2025Abstract:Submodular functions, defined on continuous or discrete domains, arise in numerous applications. We study the minimization of the difference of two submodular (DS) functions, over both domains, extending prior work restricted to set functions. We show that all functions on discrete domains and all smooth functions on continuous domains are DS. For discrete domains, we observe that DS minimization is equivalent to minimizing the difference of two convex (DC) functions, as in the set function case. We propose a novel variant of the DC Algorithm (DCA) and apply it to the resulting DC Program, obtaining comparable theoretical guarantees as in the set function case. The algorithm can be applied to continuous domains via discretization. Experiments demonstrate that our method outperforms baselines in integer compressive sensing and integer least squares.
GuidedQuant: Large Language Model Quantization via Exploiting End Loss Guidance
May 11, 2025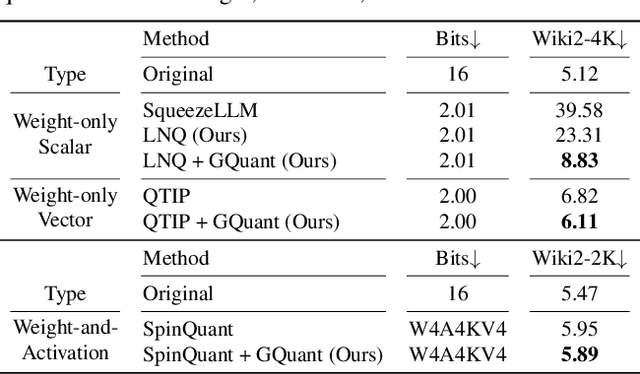
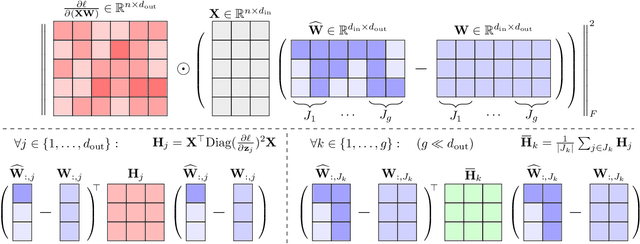
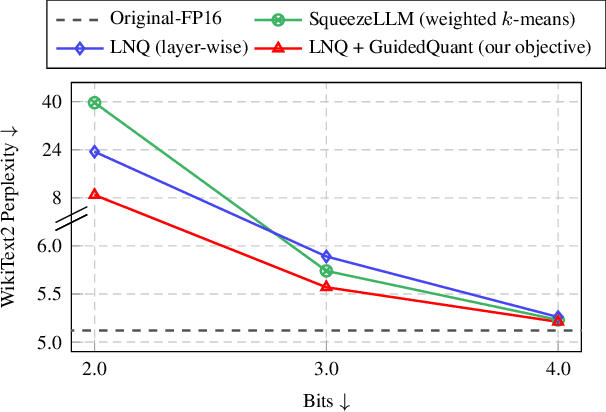
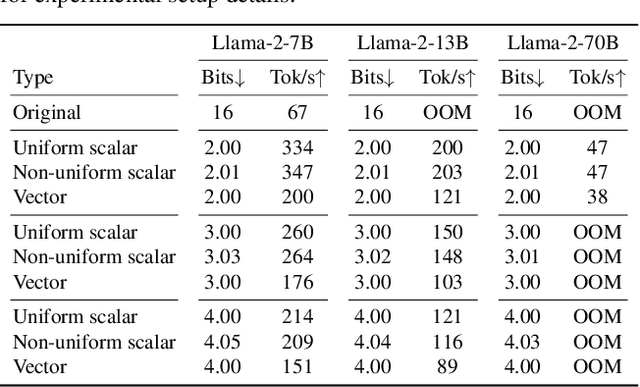
Abstract:Post-training quantization is a key technique for reducing the memory and inference latency of large language models by quantizing weights and activations without requiring retraining. However, existing methods either (1) fail to account for the varying importance of hidden features to the end loss or, when incorporating end loss, (2) neglect the critical interactions between model weights. To address these limitations, we propose GuidedQuant, a novel quantization approach that integrates gradient information from the end loss into the quantization objective while preserving cross-weight dependencies within output channels. GuidedQuant consistently boosts the performance of state-of-the-art quantization methods across weight-only scalar, weight-only vector, and weight-and-activation quantization. Additionally, we introduce a novel non-uniform scalar quantization algorithm, which is guaranteed to monotonically decrease the quantization objective value, and outperforms existing methods in this category. We release the code at https://github.com/snu-mllab/GuidedQuant.
LayerMerge: Neural Network Depth Compression through Layer Pruning and Merging
Jun 18, 2024



Abstract:Recent works show that reducing the number of layers in a convolutional neural network can enhance efficiency while maintaining the performance of the network. Existing depth compression methods remove redundant non-linear activation functions and merge the consecutive convolution layers into a single layer. However, these methods suffer from a critical drawback; the kernel size of the merged layers becomes larger, significantly undermining the latency reduction gained from reducing the depth of the network. We show that this problem can be addressed by jointly pruning convolution layers and activation functions. To this end, we propose LayerMerge, a novel depth compression method that selects which activation layers and convolution layers to remove, to achieve a desired inference speed-up while minimizing performance loss. Since the corresponding selection problem involves an exponential search space, we formulate a novel surrogate optimization problem and efficiently solve it via dynamic programming. Empirical results demonstrate that our method consistently outperforms existing depth compression and layer pruning methods on various network architectures, both on image classification and generation tasks. We release the code at https://github.com/snu-mllab/LayerMerge.
Fairness in Submodular Maximization over a Matroid Constraint
Dec 21, 2023
Abstract:Submodular maximization over a matroid constraint is a fundamental problem with various applications in machine learning. Some of these applications involve decision-making over datapoints with sensitive attributes such as gender or race. In such settings, it is crucial to guarantee that the selected solution is fairly distributed with respect to this attribute. Recently, fairness has been investigated in submodular maximization under a cardinality constraint in both the streaming and offline settings, however the more general problem with matroid constraint has only been considered in the streaming setting and only for monotone objectives. This work fills this gap. We propose various algorithms and impossibility results offering different trade-offs between quality, fairness, and generality.
Fairness in Streaming Submodular Maximization over a Matroid Constraint
May 24, 2023
Abstract:Streaming submodular maximization is a natural model for the task of selecting a representative subset from a large-scale dataset. If datapoints have sensitive attributes such as gender or race, it becomes important to enforce fairness to avoid bias and discrimination. This has spurred significant interest in developing fair machine learning algorithms. Recently, such algorithms have been developed for monotone submodular maximization under a cardinality constraint. In this paper, we study the natural generalization of this problem to a matroid constraint. We give streaming algorithms as well as impossibility results that provide trade-offs between efficiency, quality and fairness. We validate our findings empirically on a range of well-known real-world applications: exemplar-based clustering, movie recommendation, and maximum coverage in social networks.
Difference of Submodular Minimization via DC Programming
May 18, 2023



Abstract:Minimizing the difference of two submodular (DS) functions is a problem that naturally occurs in various machine learning problems. Although it is well known that a DS problem can be equivalently formulated as the minimization of the difference of two convex (DC) functions, existing algorithms do not fully exploit this connection. A classical algorithm for DC problems is called the DC algorithm (DCA). We introduce variants of DCA and its complete form (CDCA) that we apply to the DC program corresponding to DS minimization. We extend existing convergence properties of DCA, and connect them to convergence properties on the DS problem. Our results on DCA match the theoretical guarantees satisfied by existing DS algorithms, while providing a more complete characterization of convergence properties. In the case of CDCA, we obtain a stronger local minimality guarantee. Our numerical results show that our proposed algorithms outperform existing baselines on two applications: speech corpus selection and feature selection.
Data-Efficient Structured Pruning via Submodular Optimization
Mar 09, 2022



Abstract:Structured pruning is an effective approach for compressing large pre-trained neural networks without significantly affecting their performance, which involves removing redundant regular regions of weights. However, current structured pruning methods are highly empirical in nature, do not provide any theoretical guarantees, and often require fine-tuning, which makes them inapplicable in the limited-data regime. We propose a principled data-efficient structured pruning method based on submodular optimization. In particular, for a given layer, we select neurons/channels to prune and corresponding new weights for the next layer, that minimize the change in the next layer's input induced by pruning. We show that this selection problem is a weakly submodular maximization problem, thus it can be provably approximated using an efficient greedy algorithm. Our method is one of the few in the literature that uses only a limited-number of training data and no labels. Our experimental results demonstrate that our method outperforms popular baseline methods in various one-shot pruning settings.
Fairness in Streaming Submodular Maximization: Algorithms and Hardness
Oct 18, 2020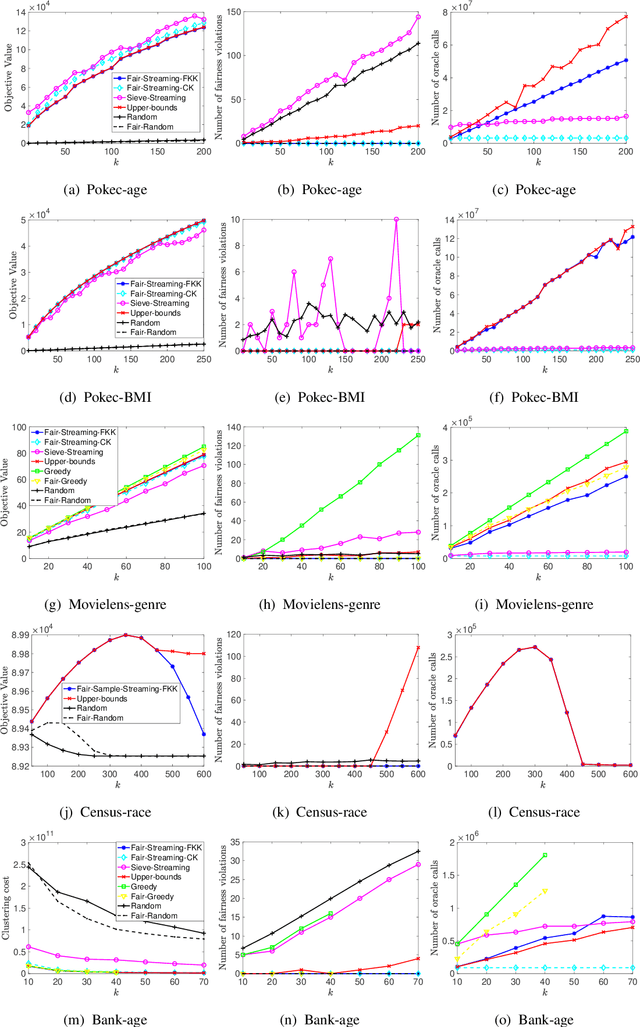
Abstract:Submodular maximization has become established as the method of choice for the task of selecting representative and diverse summaries of data. However, if datapoints have sensitive attributes such as gender or age, such machine learning algorithms, left unchecked, are known to exhibit bias: under- or over-representation of particular groups. This has made the design of fair machine learning algorithms increasingly important. In this work we address the question: Is it possible to create fair summaries for massive datasets? To this end, we develop the first streaming approximation algorithms for submodular maximization under fairness constraints, for both monotone and non-monotone functions. We validate our findings empirically on exemplar-based clustering, movie recommendation, DPP-based summarization, and maximum coverage in social networks, showing that fairness constraints do not significantly impact utility.
Minimizing approximately submodular functions
May 29, 2019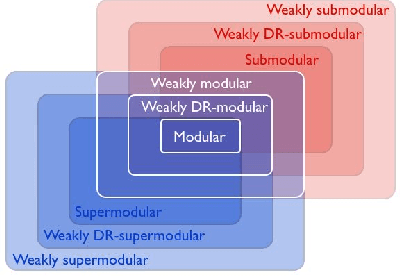

Abstract:The problem of minimizing a submodular function is well studied; several polynomial-time algorithms have been developed to solve it exactly or up to arbitrary accuracy. However, in many applications, the objective functions are not exactly submodular. In this paper, we show that a classical algorithm used for submodular minimization performs well even for a class of non-submodular functions, namely weakly DR-submodular functions. We provide the first approximation guarantee for non-submodular minimization. This broadly expands the range of applications of submodular minimization techniques.
Combinatorial Penalties: Which structures are preserved by convex relaxations?
Mar 07, 2018


Abstract:We consider the homogeneous and the non-homogeneous convex relaxations for combinatorial penalty functions defined on support sets. Our study identifies key differences in the tightness of the resulting relaxations through the notion of the lower combinatorial envelope of a set-function along with new necessary conditions for support identification. We then propose a general adaptive estimator for convex monotone regularizers, and derive new sufficient conditions for support recovery in the asymptotic setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge