Minimizing approximately submodular functions
Paper and Code
May 29, 2019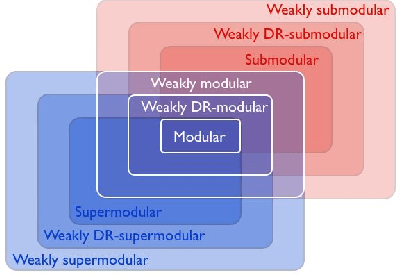
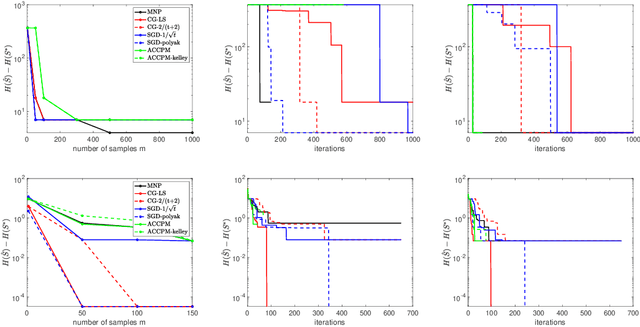

The problem of minimizing a submodular function is well studied; several polynomial-time algorithms have been developed to solve it exactly or up to arbitrary accuracy. However, in many applications, the objective functions are not exactly submodular. In this paper, we show that a classical algorithm used for submodular minimization performs well even for a class of non-submodular functions, namely weakly DR-submodular functions. We provide the first approximation guarantee for non-submodular minimization. This broadly expands the range of applications of submodular minimization techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge