Discrete and Continuous Difference of Submodular Minimization

Submodular functions, defined on continuous or discrete domains, arise in numerous applications. We study the minimization of the difference of two submodular (DS) functions, over both domains, extending prior work restricted to set functions. We show that all functions on discrete domains and all smooth functions on continuous domains are DS. For discrete domains, we observe that DS minimization is equivalent to minimizing the difference of two convex (DC) functions, as in the set function case. We propose a novel variant of the DC Algorithm (DCA) and apply it to the resulting DC Program, obtaining comparable theoretical guarantees as in the set function case. The algorithm can be applied to continuous domains via discretization. Experiments demonstrate that our method outperforms baselines in integer compressive sensing and integer least squares.

Data-Driven Priors in the Maximum Entropy on the Mean Method for Linear Inverse Problems

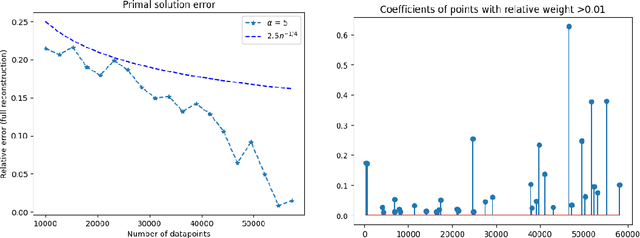
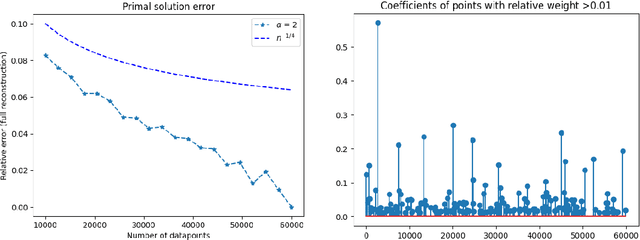
We establish the theoretical framework for implementing the maximumn entropy on the mean (MEM) method for linear inverse problems in the setting of approximate (data-driven) priors. We prove a.s. convergence for empirical means and further develop general estimates for the difference between the MEM solutions with different priors $\mu$ and $\nu$ based upon the epigraphical distance between their respective log-moment generating functions. These estimates allow us to establish a rate of convergence in expectation for empirical means. We illustrate our results with denoising on MNIST and Fashion-MNIST data sets.

Difference of Submodular Minimization via DC Programming

Minimizing the difference of two submodular (DS) functions is a problem that naturally occurs in various machine learning problems. Although it is well known that a DS problem can be equivalently formulated as the minimization of the difference of two convex (DC) functions, existing algorithms do not fully exploit this connection. A classical algorithm for DC problems is called the DC algorithm (DCA). We introduce variants of DCA and its complete form (CDCA) that we apply to the DC program corresponding to DS minimization. We extend existing convergence properties of DCA, and connect them to convergence properties on the DS problem. Our results on DCA match the theoretical guarantees satisfied by existing DS algorithms, while providing a more complete characterization of convergence properties. In the case of CDCA, we obtain a stronger local minimality guarantee. Our numerical results show that our proposed algorithms outperform existing baselines on two applications: speech corpus selection and feature selection.

Square Root LASSO: Well-posedness, Lipschitz stability and the tuning trade off

This paper studies well-posedness and parameter sensitivity of the Square Root LASSO (SR-LASSO), an optimization model for recovering sparse solutions to linear inverse problems in finite dimension. An advantage of the SR-LASSO (e.g., over the standard LASSO) is that the optimal tuning of the regularization parameter is robust with respect to measurement noise. This paper provides three point-based regularity conditions at a solution of the SR-LASSO: the weak, intermediate, and strong assumptions. It is shown that the weak assumption implies uniqueness of the solution in question. The intermediate assumption yields a directionally differentiable and locally Lipschitz solution map (with explicit Lipschitz bounds), whereas the strong assumption gives continuous differentiability of said map around the point in question. Our analysis leads to new theoretical insights on the comparison between SR-LASSO and LASSO from the viewpoint of tuning parameter sensitivity: noise-robust optimal parameter choice for SR-LASSO comes at the "price" of elevated tuning parameter sensitivity. Numerical results support and showcase the theoretical findings.

Maximum Entropy on the Mean: A Paradigm Shift for Regularization in Image Deblurring

Image deblurring is a notoriously challenging ill-posed inverse problem. In recent years, a wide variety of approaches have been proposed based upon regularization at the level of the image or on techniques from machine learning. We propose an alternative approach, shifting the paradigm towards regularization at the level of the probability distribution on the space of images. Our method is based upon the idea of maximum entropy on the mean wherein we work at the level of the probability density function of the image whose expectation is our estimate of the ground truth. Using techniques from convex analysis and probability theory, we show that the method is computationally feasible and amenable to very large blurs. Moreover, when images are imbedded with symbology (a known pattern), we show how our method can be applied to approximate the unknown blur kernel with remarkable effects. While our method is stable with respect to small amounts of noise, it does not actively denoise. However, for moderate to large amounts of noise, it performs well by preconditioned denoising with a state of the art method.

A principled approach for generating adversarial images under non-smooth dissimilarity metrics

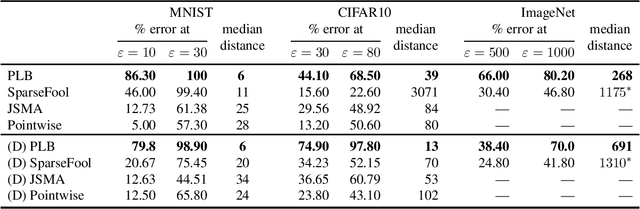
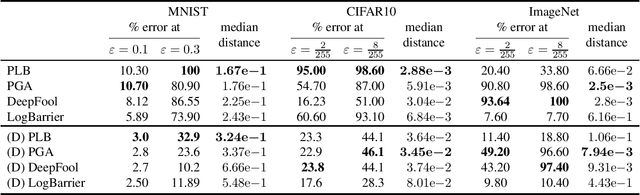
Deep neural networks are vulnerable to adversarial perturbations: small changes in the input easily lead to misclassification. In this work, we propose an attack methodology catered not only for cases where the perturbations are measured by $\ell_p$ norms, but in fact any adversarial dissimilarity metric with a closed proximal form. This includes, but is not limited to, $\ell_1$, $\ell_2$, $\ell_\infty$ perturbations, and the $\ell_0$ counting "norm", i.e. true sparseness. Our approach to generating perturbations is a natural extension of our recent work, the LogBarrier attack, which previously required the metric to be differentiable. We demonstrate our new algorithm, ProxLogBarrier, on the MNIST, CIFAR10, and ImageNet-1k datasets. We attack undefended and defended models, and show that our algorithm transfers to various datasets with little parameter tuning. In particular, in the $\ell_0$ case, our algorithm finds significantly smaller perturbations compared to multiple existing methods

Convex Geometry of the Generalized Matrix-Fractional Function

Generalized matrix-fractional (GMF) functions are a class of matrix support functions introduced by Burke and Hoheisel as a tool for unifying a range of seemingly divergent matrix optimization problems associated with inverse problems, regularization and learning. In this paper we dramatically simplify the support function representation for GMF functions as well as the representation of their subdifferentials. These new representations allow the ready computation of a range of important related geometric objects whose formulations were previously unavailable.