Orient Anything

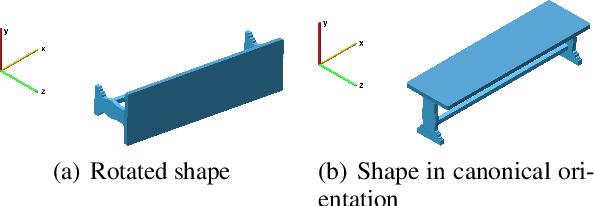
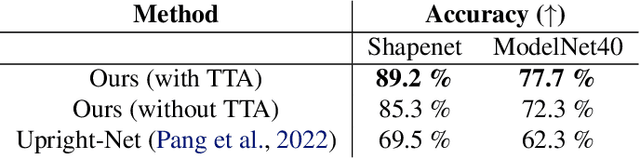
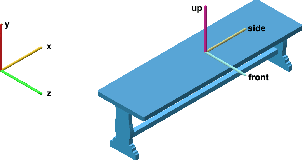
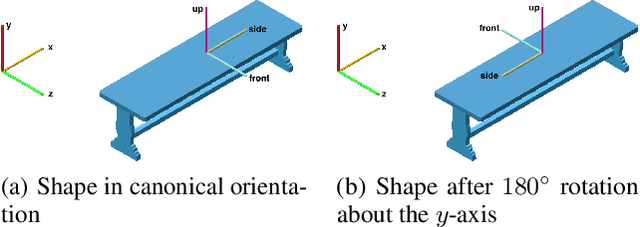
Orientation estimation is a fundamental task in 3D shape analysis which consists of estimating a shape's orientation axes: its side-, up-, and front-axes. Using this data, one can rotate a shape into canonical orientation, where its orientation axes are aligned with the coordinate axes. Developing an orientation algorithm that reliably estimates complete orientations of general shapes remains an open problem. We introduce a two-stage orientation pipeline that achieves state of the art performance on up-axis estimation and further demonstrate its efficacy on full-orientation estimation, where one seeks all three orientation axes. Unlike previous work, we train and evaluate our method on all of Shapenet rather than a subset of classes. We motivate our engineering contributions by theory describing fundamental obstacles to orientation estimation for rotationally-symmetric shapes, and show how our method avoids these obstacles.

Nuclear Norm Regularization for Deep Learning

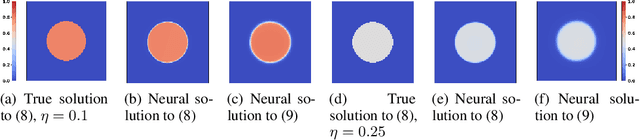
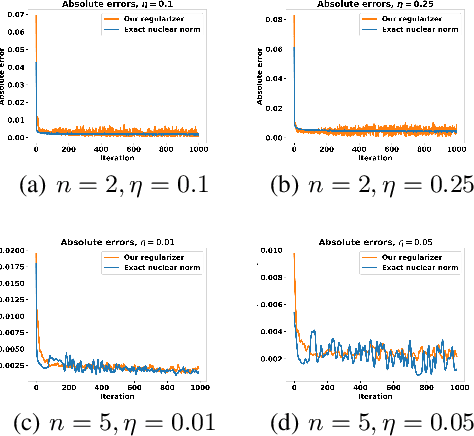
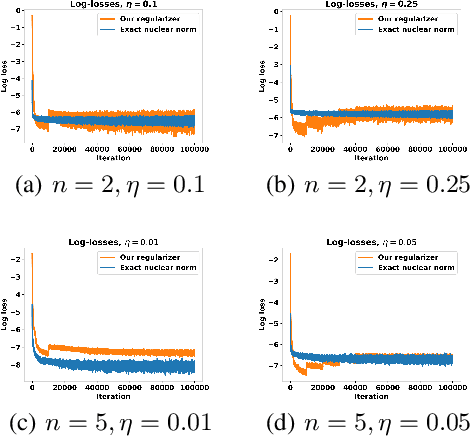
Penalizing the nuclear norm of a function's Jacobian encourages it to locally behave like a low-rank linear map. Such functions vary locally along only a handful of directions, making the Jacobian nuclear norm a natural regularizer for machine learning problems. However, this regularizer is intractable for high-dimensional problems, as it requires computing a large Jacobian matrix and taking its singular value decomposition. We show how to efficiently penalize the Jacobian nuclear norm using techniques tailor-made for deep learning. We prove that for functions parametrized as compositions $f = g \circ h$, one may equivalently penalize the average squared Frobenius norm of $Jg$ and $Jh$. We then propose a denoising-style approximation that avoids the Jacobian computations altogether. Our method is simple, efficient, and accurate, enabling Jacobian nuclear norm regularization to scale to high-dimensional deep learning problems. We complement our theory with an empirical study of our regularizer's performance and investigate applications to denoising and representation learning.

Closed-Form Diffusion Models

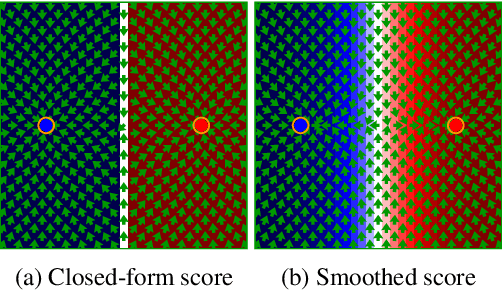
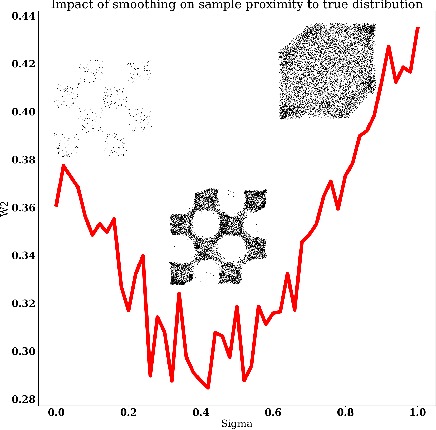
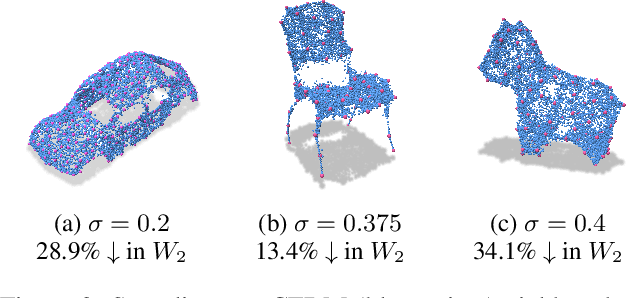
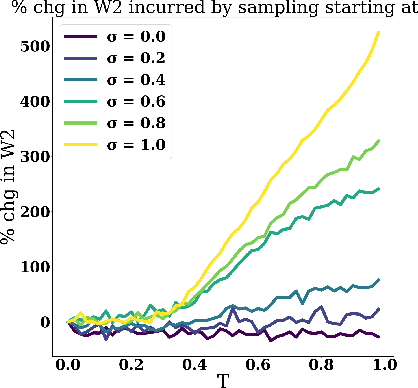
Score-based generative models (SGMs) sample from a target distribution by iteratively transforming noise using the score function of the perturbed target. For any finite training set, this score function can be evaluated in closed form, but the resulting SGM memorizes its training data and does not generate novel samples. In practice, one approximates the score by training a neural network via score-matching. The error in this approximation promotes generalization, but neural SGMs are costly to train and sample, and the effective regularization this error provides is not well-understood theoretically. In this work, we instead explicitly smooth the closed-form score to obtain an SGM that generates novel samples without training. We analyze our model and propose an efficient nearest-neighbor-based estimator of its score function. Using this estimator, our method achieves sampling times competitive with neural SGMs while running on consumer-grade CPUs.

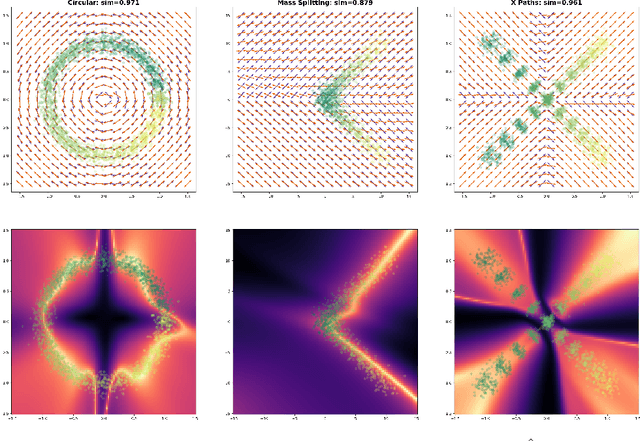
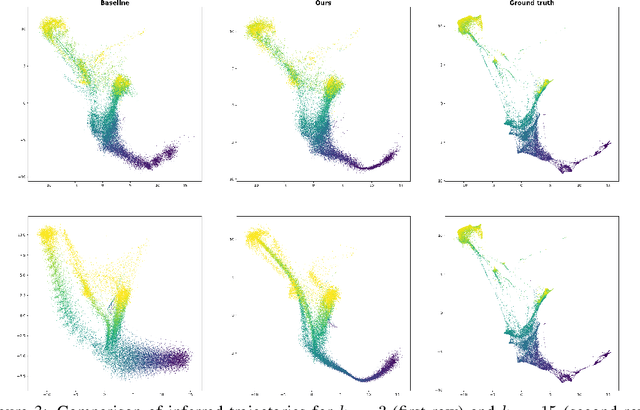
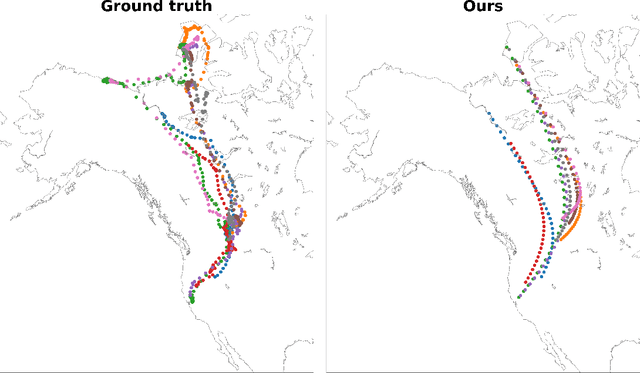
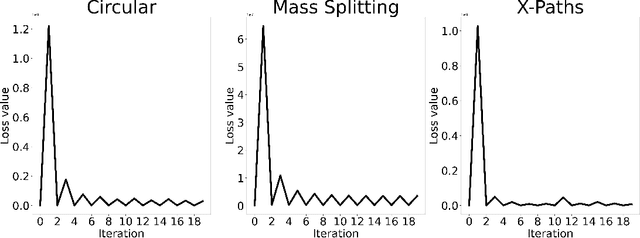
Riemannian Metric Learning via Optimal Transport

We introduce an optimal transport-based model for learning a metric tensor from cross-sectional samples of evolving probability measures on a common Riemannian manifold. We neurally parametrize the metric as a spatially-varying matrix field and efficiently optimize our model's objective using backpropagation. Using this learned metric, we can nonlinearly interpolate between probability measures and compute geodesics on the manifold. We show that metrics learned using our method improve the quality of trajectory inference on scRNA and bird migration data at the cost of little additional cross-sectional data.

Maximum Entropy on the Mean: A Paradigm Shift for Regularization in Image Deblurring

Image deblurring is a notoriously challenging ill-posed inverse problem. In recent years, a wide variety of approaches have been proposed based upon regularization at the level of the image or on techniques from machine learning. We propose an alternative approach, shifting the paradigm towards regularization at the level of the probability distribution on the space of images. Our method is based upon the idea of maximum entropy on the mean wherein we work at the level of the probability density function of the image whose expectation is our estimate of the ground truth. Using techniques from convex analysis and probability theory, we show that the method is computationally feasible and amenable to very large blurs. Moreover, when images are imbedded with symbology (a known pattern), we show how our method can be applied to approximate the unknown blur kernel with remarkable effects. While our method is stable with respect to small amounts of noise, it does not actively denoise. However, for moderate to large amounts of noise, it performs well by preconditioned denoising with a state of the art method.