Riemannian Metric Learning via Optimal Transport
Paper and Code
May 18, 2022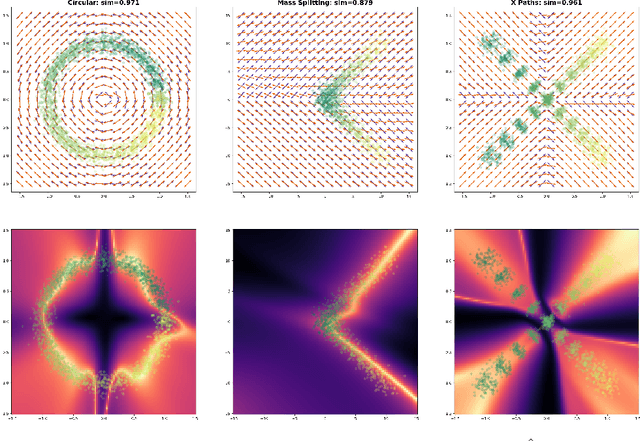
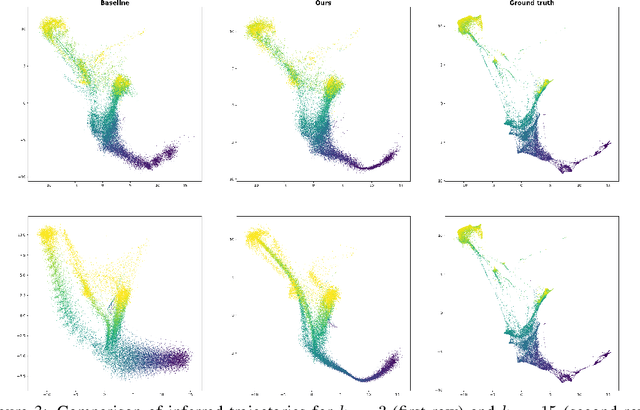
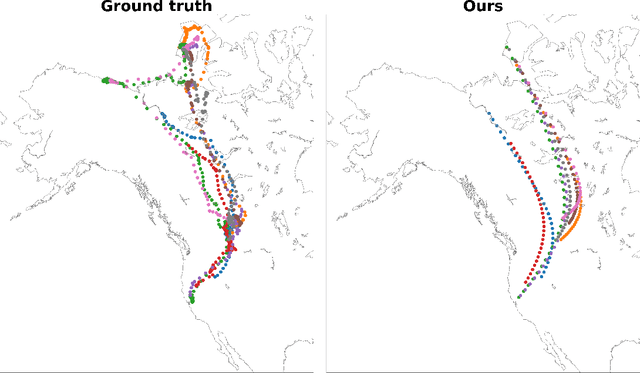
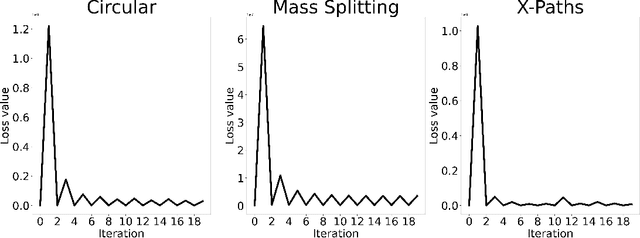
We introduce an optimal transport-based model for learning a metric tensor from cross-sectional samples of evolving probability measures on a common Riemannian manifold. We neurally parametrize the metric as a spatially-varying matrix field and efficiently optimize our model's objective using backpropagation. Using this learned metric, we can nonlinearly interpolate between probability measures and compute geodesics on the manifold. We show that metrics learned using our method improve the quality of trajectory inference on scRNA and bird migration data at the cost of little additional cross-sectional data.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge