Data-Driven Priors in the Maximum Entropy on the Mean Method for Linear Inverse Problems

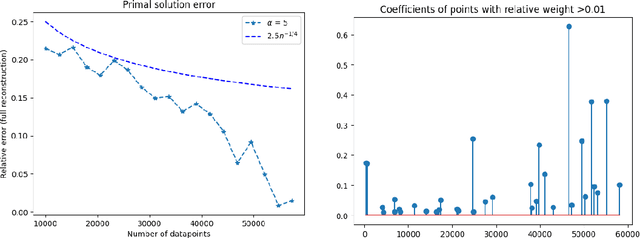
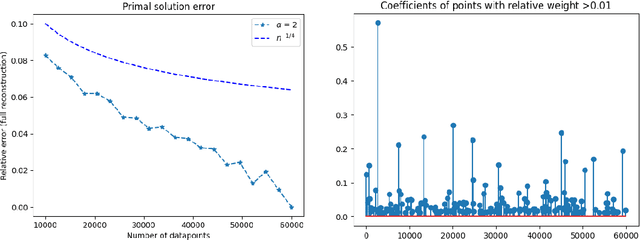
We establish the theoretical framework for implementing the maximumn entropy on the mean (MEM) method for linear inverse problems in the setting of approximate (data-driven) priors. We prove a.s. convergence for empirical means and further develop general estimates for the difference between the MEM solutions with different priors $\mu$ and $\nu$ based upon the epigraphical distance between their respective log-moment generating functions. These estimates allow us to establish a rate of convergence in expectation for empirical means. We illustrate our results with denoising on MNIST and Fashion-MNIST data sets.

Maximum Entropy on the Mean: A Paradigm Shift for Regularization in Image Deblurring

Image deblurring is a notoriously challenging ill-posed inverse problem. In recent years, a wide variety of approaches have been proposed based upon regularization at the level of the image or on techniques from machine learning. We propose an alternative approach, shifting the paradigm towards regularization at the level of the probability distribution on the space of images. Our method is based upon the idea of maximum entropy on the mean wherein we work at the level of the probability density function of the image whose expectation is our estimate of the ground truth. Using techniques from convex analysis and probability theory, we show that the method is computationally feasible and amenable to very large blurs. Moreover, when images are imbedded with symbology (a known pattern), we show how our method can be applied to approximate the unknown blur kernel with remarkable effects. While our method is stable with respect to small amounts of noise, it does not actively denoise. However, for moderate to large amounts of noise, it performs well by preconditioned denoising with a state of the art method.

A Regularization Approach to Blind Deblurring and Denoising of QR Barcodes

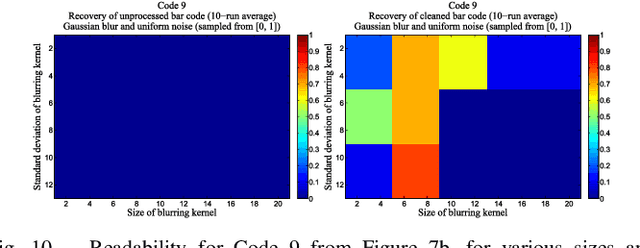
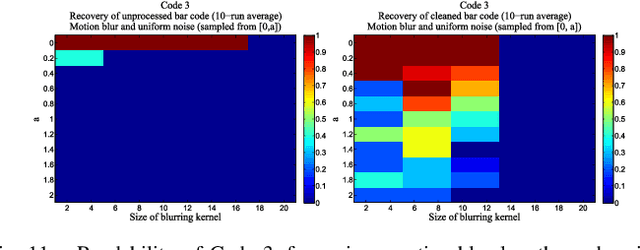
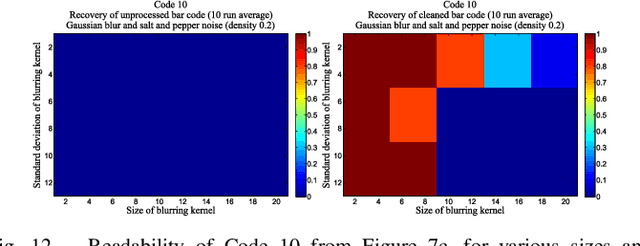
QR bar codes are prototypical images for which part of the image is a priori known (required patterns). Open source bar code readers, such as ZBar, are readily available. We exploit both these facts to provide and assess purely regularization-based methods for blind deblurring of QR bar codes in the presence of noise.