Variational inference via radial transport

In variational inference (VI), the practitioner approximates a high-dimensional distribution $π$ with a simple surrogate one, often a (product) Gaussian distribution. However, in many cases of practical interest, Gaussian distributions might not capture the correct radial profile of $π$, resulting in poor coverage. In this work, we approach the VI problem from the perspective of optimizing over these radial profiles. Our algorithm radVI is a cheap, effective add-on to many existing VI schemes, such as Gaussian (mean-field) VI and Laplace approximation. We provide theoretical convergence guarantees for our algorithm, owing to recent developments in optimization over the Wasserstein space--the space of probability distributions endowed with the Wasserstein distance--and new regularity properties of radial transport maps in the style of Caffarelli (2000).

Blind denoising diffusion models and the blessings of dimensionality

We analyze, theoretically and empirically, the performance of generative diffusion models based on \emph{blind denoisers}, in which the denoiser is not given the noise amplitude in either the training or sampling processes. Assuming that the data distribution has low intrinsic dimensionality, we prove that blind denoising diffusion models (BDDMs), despite not having access to the noise amplitude, \emph{automatically} track a particular \emph{implicit} noise schedule along the reverse process. Our analysis shows that BDDMs can accurately sample from the data distribution in polynomially many steps as a function of the intrinsic dimension. Empirical results corroborate these mathematical findings on both synthetic and image data, demonstrating that the noise variance is accurately estimated from the noisy image. Remarkably, we observe that schedule-free BDDMs produce samples of higher quality compared to their non-blind counterparts. We provide evidence that this performance gain arises because BDDMs correct the mismatch between the true residual noise (of the image) and the noise assumed by the schedule used in non-blind diffusion models.

Theory and computation for structured variational inference

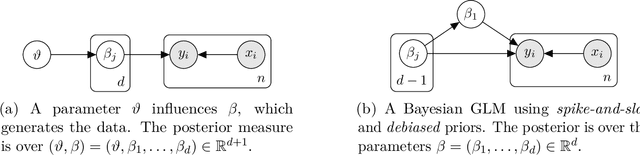
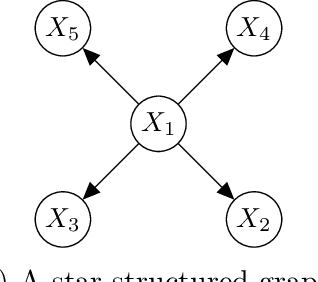
Structured variational inference constitutes a core methodology in modern statistical applications. Unlike mean-field variational inference, the approximate posterior is assumed to have interdependent structure. We consider the natural setting of star-structured variational inference, where a root variable impacts all the other ones. We prove the first results for existence, uniqueness, and self-consistency of the variational approximation. In turn, we derive quantitative approximation error bounds for the variational approximation to the posterior, extending prior work from the mean-field setting to the star-structured setting. We also develop a gradient-based algorithm with provable guarantees for computing the variational approximation using ideas from optimal transport theory. We explore the implications of our results for Gaussian measures and hierarchical Bayesian models, including generalized linear models with location family priors and spike-and-slab priors with one-dimensional debiasing. As a by-product of our analysis, we develop new stability results for star-separable transport maps which might be of independent interest.

Conditional simulation via entropic optimal transport: Toward non-parametric estimation of conditional Brenier maps

Conditional simulation is a fundamental task in statistical modeling: Generate samples from the conditionals given finitely many data points from a joint distribution. One promising approach is to construct conditional Brenier maps, where the components of the map pushforward a reference distribution to conditionals of the target. While many estimators exist, few, if any, come with statistical or algorithmic guarantees. To this end, we propose a non-parametric estimator for conditional Brenier maps based on the computational scalability of \emph{entropic} optimal transport. Our estimator leverages a result of Carlier et al. (2010), which shows that optimal transport maps under a rescaled quadratic cost asymptotically converge to conditional Brenier maps; our estimator is precisely the entropic analogues of these converging maps. We provide heuristic justifications for choosing the scaling parameter in the cost as a function of the number of samples by fully characterizing the Gaussian setting. We conclude by comparing the performance of the estimator to other machine learning and non-parametric approaches on benchmark datasets and Bayesian inference problems.

Wasserstein Flow Matching: Generative modeling over families of distributions

Generative modeling typically concerns the transport of a single source distribution to a single target distribution by learning (i.e., regressing onto) simple probability flows. However, in modern data-driven fields such as computer graphics and single-cell genomics, samples (say, point-clouds) from datasets can themselves be viewed as distributions (as, say, discrete measures). In these settings, the standard generative modeling paradigm of flow matching would ignore the relevant geometry of the samples. To remedy this, we propose \emph{Wasserstein flow matching} (WFM), which appropriately lifts flow matching onto families of distributions by appealing to the Riemannian nature of the Wasserstein geometry. Our algorithm leverages theoretical and computational advances in (entropic) optimal transport, as well as the attention mechanism in our neural network architecture. We present two novel algorithmic contributions. First, we demonstrate how to perform generative modeling over Gaussian distributions, where we generate representations of granular cell states from single-cell genomics data. Secondly, we show that WFM can learn flows between high-dimensional and variable sized point-clouds and synthesize cellular microenvironments from spatial transcriptomics datasets. Code is available at [WassersteinFlowMatching](https://github.com/DoronHav/WassersteinFlowMatching).

Plug-in estimation of Schrödinger bridges

We propose a procedure for estimating the Schr\"odinger bridge between two probability distributions. Unlike existing approaches, our method does not require iteratively simulating forward and backward diffusions or training neural networks to fit unknown drifts. Instead, we show that the potentials obtained from solving the static entropic optimal transport problem between the source and target samples can be modified to yield a natural plug-in estimator of the time-dependent drift that defines the bridge between two measures. Under minimal assumptions, we show that our proposal, which we call the \emph{Sinkhorn bridge}, provably estimates the Schr\"odinger bridge with a rate of convergence that depends on the intrinsic dimensionality of the target measure. Our approach combines results from the areas of sampling, and theoretical and statistical entropic optimal transport.

Progressive Entropic Optimal Transport Solvers

Optimal transport (OT) has profoundly impacted machine learning by providing theoretical and computational tools to realign datasets. In this context, given two large point clouds of sizes $n$ and $m$ in $\mathbb{R}^d$, entropic OT (EOT) solvers have emerged as the most reliable tool to either solve the Kantorovich problem and output a $n\times m$ coupling matrix, or to solve the Monge problem and learn a vector-valued push-forward map. While the robustness of EOT couplings/maps makes them a go-to choice in practical applications, EOT solvers remain difficult to tune because of a small but influential set of hyperparameters, notably the omnipresent entropic regularization strength $\varepsilon$. Setting $\varepsilon$ can be difficult, as it simultaneously impacts various performance metrics, such as compute speed, statistical performance, generalization, and bias. In this work, we propose a new class of EOT solvers (ProgOT), that can estimate both plans and transport maps. We take advantage of several opportunities to optimize the computation of EOT solutions by dividing mass displacement using a time discretization, borrowing inspiration from dynamic OT formulations, and conquering each of these steps using EOT with properly scheduled parameters. We provide experimental evidence demonstrating that ProgOT is a faster and more robust alternative to standard solvers when computing couplings at large scales, even outperforming neural network-based approaches. We also prove statistical consistency of our approach for estimating optimal transport maps.

Neural Optimal Transport with Lagrangian Costs

We investigate the optimal transport problem between probability measures when the underlying cost function is understood to satisfy a least action principle, also known as a Lagrangian cost. These generalizations are useful when connecting observations from a physical system where the transport dynamics are influenced by the geometry of the system, such as obstacles (e.g., incorporating barrier functions in the Lagrangian), and allows practitioners to incorporate a priori knowledge of the underlying system such as non-Euclidean geometries (e.g., paths must be circular). Our contributions are of computational interest, where we demonstrate the ability to efficiently compute geodesics and amortize spline-based paths, which has not been done before, even in low dimensional problems. Unlike prior work, we also output the resulting Lagrangian optimal transport map without requiring an ODE solver. We demonstrate the effectiveness of our formulation on low-dimensional examples taken from prior work. The source code to reproduce our experiments is available at https://github.com/facebookresearch/lagrangian-ot.

Algorithms for mean-field variational inference via polyhedral optimization in the Wasserstein space

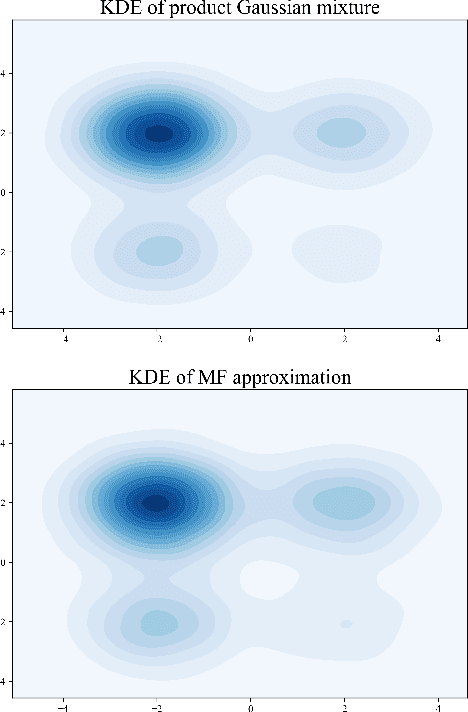
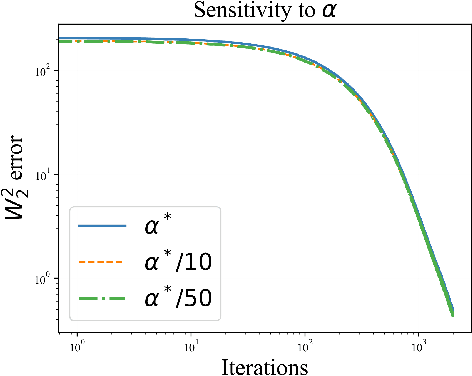
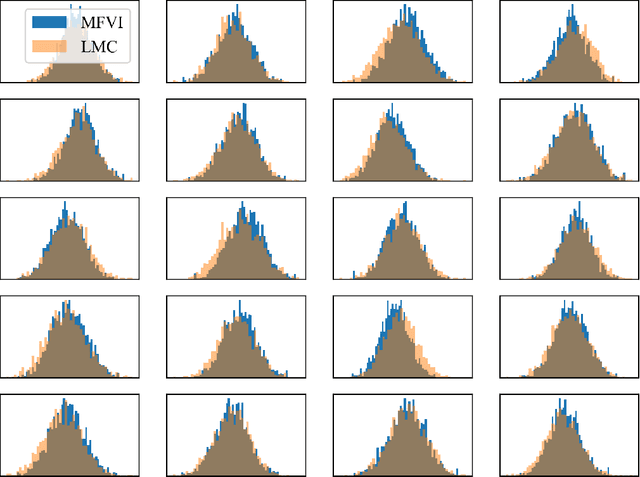
We develop a theory of finite-dimensional polyhedral subsets over the Wasserstein space and optimization of functionals over them via first-order methods. Our main application is to the problem of mean-field variational inference, which seeks to approximate a distribution $\pi$ over $\mathbb{R}^d$ by a product measure $\pi^\star$. When $\pi$ is strongly log-concave and log-smooth, we provide (1) approximation rates certifying that $\pi^\star$ is close to the minimizer $\pi^\star_\diamond$ of the KL divergence over a \emph{polyhedral} set $\mathcal{P}_\diamond$, and (2) an algorithm for minimizing $\text{KL}(\cdot\|\pi)$ over $\mathcal{P}_\diamond$ with accelerated complexity $O(\sqrt \kappa \log(\kappa d/\varepsilon^2))$, where $\kappa$ is the condition number of $\pi$.

Learning Costs for Structured Monge Displacements

Optimal transport theory has provided machine learning with several tools to infer a push-forward map between densities from samples. While this theory has recently seen tremendous methodological developments in machine learning, its practical implementation remains notoriously difficult, because it is plagued by both computational and statistical challenges. Because of such difficulties, existing approaches rarely depart from the default choice of estimating such maps with the simple squared-Euclidean distance as the ground cost, $c(x,y)=\|x-y\|^2_2$. We follow a different path in this work, with the motivation of \emph{learning} a suitable cost structure to encourage maps to transport points along engineered features. We extend the recently proposed Monge-Bregman-Occam pipeline~\citep{cuturi2023monge}, that rests on an alternative cost formulation that is also cost-invariant $c(x,y)=h(x-y)$, but which adopts a more general form as $h=\tfrac12 \ell_2^2+\tau$, where $\tau$ is an appropriately chosen regularizer. We first propose a method that builds upon proximal gradient descent to generate ground truth transports for such structured costs, using the notion of $h$-transforms and $h$-concave potentials. We show more generally that such a method can be extended to compute $h$-transforms for entropic potentials. We study a regularizer that promotes transport displacements in low-dimensional spaces, and propose to learn such a basis change using Riemannian gradient descent on the Stiefel manifold. We show that these changes lead to estimators that are more robust and easier to interpret.