Yiheng Jiang
LuSeeL: Language-queried Binaural Universal Sound Event Extraction and Localization
Jan 27, 2026Abstract:Most universal sound extraction algorithms focus on isolating a target sound event from single-channel audio mixtures. However, the real world is three-dimensional, and binaural audio, which mimics human hearing, can capture richer spatial information, including sound source location. This spatial context is crucial for understanding and modeling complex auditory scenes, as it inherently informs sound detection and extraction. In this work, we propose a language-driven universal sound extraction network that isolates text-described sound events from binaural mixtures by effectively leveraging the spatial cues present in binaural signals. Additionally, we jointly predict the direction of arrival (DoA) of the target sound using spatial features from the extraction network. This dual-task approach exploits complementary location information to improve extraction performance while enabling accurate DoA estimation. Experimental results on the in-the-wild AudioCaps dataset show that our proposed LuSeeL model significantly outperforms single-channel and uni-task baselines.
FlowSE-GRPO: Training Flow Matching Speech Enhancement via Online Reinforcement Learning
Jan 23, 2026Abstract:Generative speech enhancement offers a promising alternative to traditional discriminative methods by modeling the distribution of clean speech conditioned on noisy inputs. Post-training alignment via reinforcement learning (RL) effectively aligns generative models with human preferences and downstream metrics in domains such as natural language processing, but its use in speech enhancement remains limited, especially for online RL. Prior work explores offline methods like Direct Preference Optimization (DPO); online methods such as Group Relative Policy Optimization (GRPO) remain largely uninvestigated. In this paper, we present the first successful integration of online GRPO into a flow-matching speech enhancement framework, enabling efficient post-training alignment to perceptual and task-oriented metrics with few update steps. Unlike prior GRPO work on Large Language Models, we adapt the algorithm to the continuous, time-series nature of speech and to the dynamics of flow-matching generative models. We show that optimizing a single reward yields rapid metric gains but often induces reward hacking that degrades audio fidelity despite higher scores. To mitigate this, we propose a multi-metric reward optimization strategy that balances competing objectives, substantially reducing overfitting and improving overall performance. Our experiments validate online GRPO for speech enhancement and provide practical guidance for RL-based post-training of generative audio models.
E2E-AEC: Implementing an end-to-end neural network learning approach for acoustic echo cancellation
Jan 23, 2026Abstract:We propose a novel neural network-based end-to-end acoustic echo cancellation (E2E-AEC) method capable of streaming inference, which operates effectively without reliance on traditional linear AEC (LAEC) techniques and time delay estimation. Our approach includes several key strategies: First, we introduce and refine progressive learning to gradually enhance echo suppression. Second, our model employs knowledge transfer by initializing with a pre-trained LAECbased model, harnessing the insights gained from LAEC training. Third, we optimize the attention mechanism with a loss function applied on attention weights to achieve precise time alignment between the reference and microphone signals. Lastly, we incorporate voice activity detection to enhance speech quality and improve echo removal by masking the network output when near-end speech is absent. The effectiveness of our approach is validated through experiments conducted on public datasets.
FunAudio-ASR Technical Report
Sep 15, 2025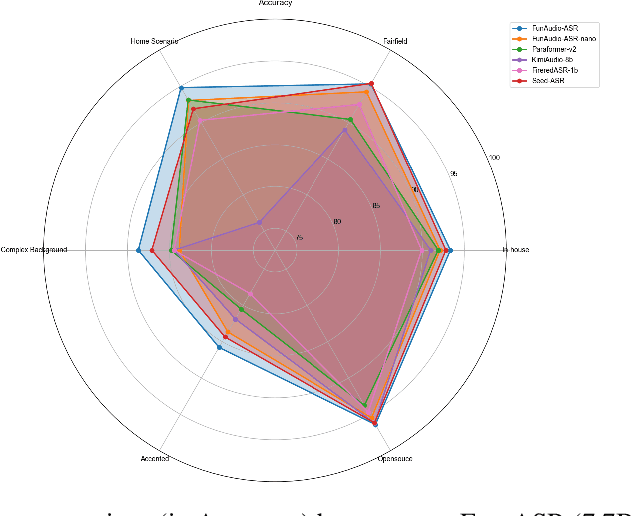
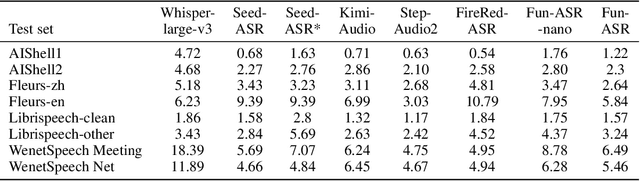
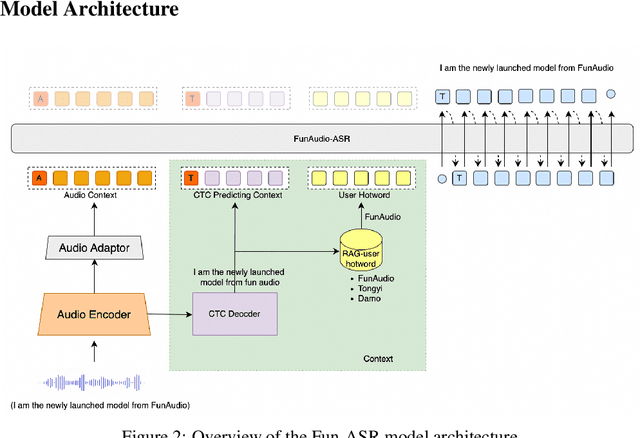
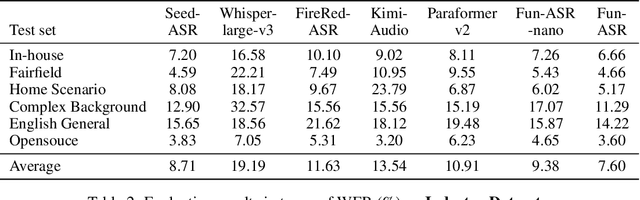
Abstract:In recent years, automatic speech recognition (ASR) has witnessed transformative advancements driven by three complementary paradigms: data scaling, model size scaling, and deep integration with large language models (LLMs). However, LLMs are prone to hallucination, which can significantly degrade user experience in real-world ASR applications. In this paper, we present FunAudio-ASR, a large-scale, LLM-based ASR system that synergistically combines massive data, large model capacity, LLM integration, and reinforcement learning to achieve state-of-the-art performance across diverse and complex speech recognition scenarios. Moreover, FunAudio-ASR is specifically optimized for practical deployment, with enhancements in streaming capability, noise robustness, code-switching, hotword customization, and satisfying other real-world application requirements. Experimental results show that while most LLM-based ASR systems achieve strong performance on open-source benchmarks, they often underperform on real industry evaluation sets. Thanks to production-oriented optimizations, FunAudio-ASR achieves SOTA performance on real application datasets, demonstrating its effectiveness and robustness in practical settings.
FLASepformer: Efficient Speech Separation with Gated Focused Linear Attention Transformer
Aug 27, 2025Abstract:Speech separation always faces the challenge of handling prolonged time sequences. Past methods try to reduce sequence lengths and use the Transformer to capture global information. However, due to the quadratic time complexity of the attention module, memory usage and inference time still increase significantly with longer segments. To tackle this, we introduce Focused Linear Attention and build FLASepformer with linear complexity for efficient speech separation. Inspired by SepReformer and TF-Locoformer, we have two variants: FLA-SepReformer and FLA-TFLocoformer. We also add a new Gated module to improve performance further. Experimental results on various datasets show that FLASepformer matches state-of-the-art performance with less memory consumption and faster inference. FLA-SepReformer-T/B/L increases speed by 2.29x, 1.91x, and 1.49x, with 15.8%, 20.9%, and 31.9% GPU memory usage, proving our model's effectiveness.
Exploring Efficient Directional and Distance Cues for Regional Speech Separation
Aug 11, 2025Abstract:In this paper, we introduce a neural network-based method for regional speech separation using a microphone array. This approach leverages novel spatial cues to extract the sound source not only from specified direction but also within defined distance. Specifically, our method employs an improved delay-and-sum technique to obtain directional cues, substantially enhancing the signal from the target direction. We further enhance separation by incorporating the direct-to-reverberant ratio into the input features, enabling the model to better discriminate sources within and beyond a specified distance. Experimental results demonstrate that our proposed method leads to substantial gains across multiple objective metrics. Furthermore, our method achieves state-of-the-art performance on the CHiME-8 MMCSG dataset, which was recorded in real-world conversational scenarios, underscoring its effectiveness for speech separation in practical applications.
A Small-footprint Acoustic Echo Cancellation Solution for Mobile Full-Duplex Speech Interactions
Aug 11, 2025Abstract:In full-duplex speech interaction systems, effective Acoustic Echo Cancellation (AEC) is crucial for recovering echo-contaminated speech. This paper presents a neural network-based AEC solution to address challenges in mobile scenarios with varying hardware, nonlinear distortions and long latency. We first incorporate diverse data augmentation strategies to enhance the model's robustness across various environments. Moreover, progressive learning is employed to incrementally improve AEC effectiveness, resulting in a considerable improvement in speech quality. To further optimize AEC's downstream applications, we introduce a novel post-processing strategy employing tailored parameters designed specifically for tasks such as Voice Activity Detection (VAD) and Automatic Speech Recognition (ASR), thus enhancing their overall efficacy. Finally, our method employs a small-footprint model with streaming inference, enabling seamless deployment on mobile devices. Empirical results demonstrate effectiveness of the proposed method in Echo Return Loss Enhancement and Perceptual Evaluation of Speech Quality, alongside significant improvements in both VAD and ASR results.
Unlocking the Power of Diffusion Models in Sequential Recommendation: A Simple and Effective Approach
May 26, 2025



Abstract:In this paper, we focus on the often-overlooked issue of embedding collapse in existing diffusion-based sequential recommendation models and propose ADRec, an innovative framework designed to mitigate this problem. Diverging from previous diffusion-based methods, ADRec applies an independent noise process to each token and performs diffusion across the entire target sequence during training. ADRec captures token interdependency through auto-regression while modeling per-token distributions through token-level diffusion. This dual approach enables the model to effectively capture both sequence dynamics and item representations, overcoming the limitations of existing methods. To further mitigate embedding collapse, we propose a three-stage training strategy: (1) pre-training the embedding weights, (2) aligning these weights with the ADRec backbone, and (3) fine-tuning the model. During inference, ADRec applies the denoising process only to the last token, ensuring that the meaningful patterns in historical interactions are preserved. Our comprehensive empirical evaluation across six datasets underscores the effectiveness of ADRec in enhancing both the accuracy and efficiency of diffusion-based sequential recommendation systems.
Pushing the Frontiers of Self-Distillation Prototypes Network with Dimension Regularization and Score Normalization
May 20, 2025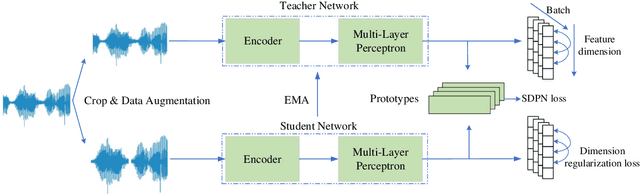
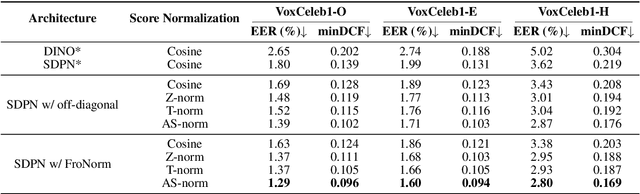

Abstract:Developing robust speaker verification (SV) systems without speaker labels has been a longstanding challenge. Earlier research has highlighted a considerable performance gap between self-supervised and fully supervised approaches. In this paper, we enhance the non-contrastive self-supervised framework, Self-Distillation Prototypes Network (SDPN), by introducing dimension regularization that explicitly addresses the collapse problem through the application of regularization terms to speaker embeddings. Moreover, we integrate score normalization techniques from fully supervised SV to further bridge the gap toward supervised verification performance. SDPN with dimension regularization and score normalization sets a new state-of-the-art on the VoxCeleb1 speaker verification evaluation benchmark, achieving Equal Error Rate 1.29%, 1.60%, and 2.80% for trial VoxCeleb1-{O,E,H} respectively. These results demonstrate relative improvements of 28.3%, 19.6%, and 22.6% over the current best self-supervised methods, thereby advancing the frontiers of SV technology.
Sparse Point Clouds Assisted Learned Image Compression
Dec 20, 2024



Abstract:In the field of autonomous driving, a variety of sensor data types exist, each representing different modalities of the same scene. Therefore, it is feasible to utilize data from other sensors to facilitate image compression. However, few techniques have explored the potential benefits of utilizing inter-modality correlations to enhance the image compression performance. In this paper, motivated by the recent success of learned image compression, we propose a new framework that uses sparse point clouds to assist in learned image compression in the autonomous driving scenario. We first project the 3D sparse point cloud onto a 2D plane, resulting in a sparse depth map. Utilizing this depth map, we proceed to predict camera images. Subsequently, we use these predicted images to extract multi-scale structural features. These features are then incorporated into learned image compression pipeline as additional information to improve the compression performance. Our proposed framework is compatible with various mainstream learned image compression models, and we validate our approach using different existing image compression methods. The experimental results show that incorporating point cloud assistance into the compression pipeline consistently enhances the performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge