Wasserstein Flow Matching: Generative modeling over families of distributions

Generative modeling typically concerns the transport of a single source distribution to a single target distribution by learning (i.e., regressing onto) simple probability flows. However, in modern data-driven fields such as computer graphics and single-cell genomics, samples (say, point-clouds) from datasets can themselves be viewed as distributions (as, say, discrete measures). In these settings, the standard generative modeling paradigm of flow matching would ignore the relevant geometry of the samples. To remedy this, we propose \emph{Wasserstein flow matching} (WFM), which appropriately lifts flow matching onto families of distributions by appealing to the Riemannian nature of the Wasserstein geometry. Our algorithm leverages theoretical and computational advances in (entropic) optimal transport, as well as the attention mechanism in our neural network architecture. We present two novel algorithmic contributions. First, we demonstrate how to perform generative modeling over Gaussian distributions, where we generate representations of granular cell states from single-cell genomics data. Secondly, we show that WFM can learn flows between high-dimensional and variable sized point-clouds and synthesize cellular microenvironments from spatial transcriptomics datasets. Code is available at [WassersteinFlowMatching](https://github.com/DoronHav/WassersteinFlowMatching).

Wasserstein Wormhole: Scalable Optimal Transport Distance with Transformers

Optimal transport (OT) and the related Wasserstein metric (W) are powerful and ubiquitous tools for comparing distributions. However, computing pairwise Wasserstein distances rapidly becomes intractable as cohort size grows. An attractive alternative would be to find an embedding space in which pairwise Euclidean distances map to OT distances, akin to standard multidimensional scaling (MDS). We present Wasserstein Wormhole, a transformer-based autoencoder that embeds empirical distributions into a latent space wherein Euclidean distances approximate OT distances. Extending MDS theory, we show that our objective function implies a bound on the error incurred when embedding non-Euclidean distances. Empirically, distances between Wormhole embeddings closely match Wasserstein distances, enabling linear time computation of OT distances. Along with an encoder that maps distributions to embeddings, Wasserstein Wormhole includes a decoder that maps embeddings back to distributions, allowing for operations in the embedding space to generalize to OT spaces, such as Wasserstein barycenter estimation and OT interpolation. By lending scalability and interpretability to OT approaches, Wasserstein Wormhole unlocks new avenues for data analysis in the fields of computational geometry and single-cell biology.

Gradient Estimation for Binary Latent Variables via Gradient Variance Clipping

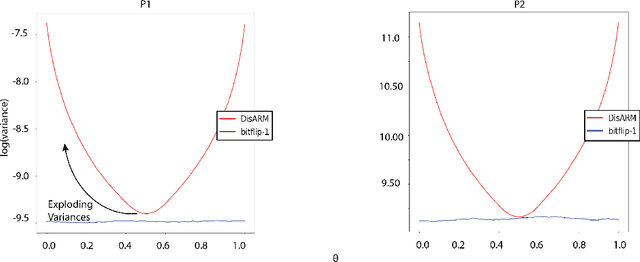
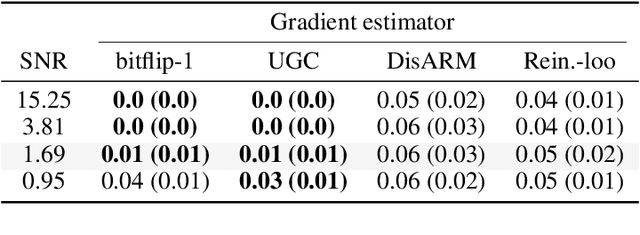
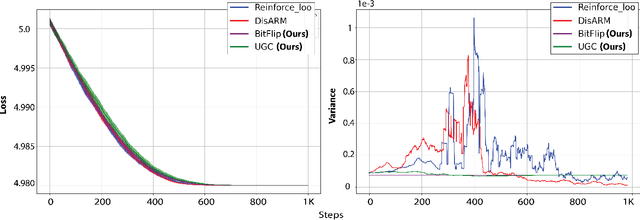
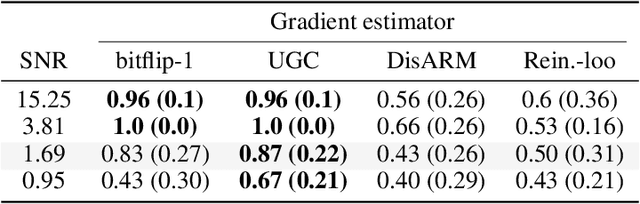
Gradient estimation is often necessary for fitting generative models with discrete latent variables, in contexts such as reinforcement learning and variational autoencoder (VAE) training. The DisARM estimator (Yin et al. 2020; Dong, Mnih, and Tucker 2020) achieves state of the art gradient variance for Bernoulli latent variable models in many contexts. However, DisARM and other estimators have potentially exploding variance near the boundary of the parameter space, where solutions tend to lie. To ameliorate this issue, we propose a new gradient estimator \textit{bitflip}-1 that has lower variance at the boundaries of the parameter space. As bitflip-1 has complementary properties to existing estimators, we introduce an aggregated estimator, \textit{unbiased gradient variance clipping} (UGC) that uses either a bitflip-1 or a DisARM gradient update for each coordinate. We theoretically prove that UGC has uniformly lower variance than DisARM. Empirically, we observe that UGC achieves the optimal value of the optimization objectives in toy experiments, discrete VAE training, and in a best subset selection problem.

The Ramanujan Machine: Automatically Generated Conjectures on Fundamental Constants

Fundamental mathematical constants like $e$ and $\pi$ are ubiquitous in diverse fields of science, from abstract mathematics and geometry to physics, biology and chemistry. Nevertheless, for centuries new mathematical formulas relating fundamental constants have been scarce and usually discovered sporadically. In this paper we propose a novel and systematic approach that leverages algorithms for deriving mathematical formulas for fundamental constants and help reveal their underlying structure. Our algorithms find dozens of well-known as well as previously unknown continued fraction representations of $\pi$, $e$, and the Riemann zeta function values. Two conjectures produced by our algorithm, along with many others, are: \begin{equation*} \frac{e}{e-2} = 4 - \frac{1}{5-\frac{2}{6-\frac{3}{7-\frac{4}{8-\ldots}}}} \quad\quad,\quad\quad \frac{4}{3\pi-8} = 3-\frac{1\cdot1}{6-\frac{2\cdot3}{9-\frac{3\cdot5}{12-\frac{4\cdot 7}{15-\ldots}}}} \end{equation*} We present two algorithms that proved useful in finding conjectures: a variant of the Meet-In-The-Middle (MITM) algorithm and a Gradient Descent (GD) tailored to the recurrent structure of continued fractions. Both algorithms are based on matching numerical values and thus they conjecture formulas without providing proofs and without requiring any prior knowledge on any underlaying mathematical structure. This approach is especially attractive for fundamental constants for which no mathematical structure is known, as it reverses the conventional approach of sequential logic in formal proofs. Instead, our work supports a different conceptual approach for research: computer algorithms utilizing numerical data to unveil mathematical structures, thus trying to play the role of intuition of great mathematicians of the past, providing leads to new mathematical research.

Understanding and Controlling Memory in Recurrent Neural Networks

To be effective in sequential data processing, Recurrent Neural Networks (RNNs) are required to keep track of past events by creating memories. While the relation between memories and the network's hidden state dynamics was established over the last decade, previous works in this direction were of a predominantly descriptive nature focusing mainly on locating the dynamical objects of interest. In particular, it remained unclear how dynamical observables affect the performance, how they form and whether they can be manipulated. Here, we utilize different training protocols, datasets and architectures to obtain a range of networks solving a delayed classification task with similar performance, alongside substantial differences in their ability to extrapolate for longer delays. We analyze the dynamics of the network's hidden state, and uncover the reasons for this difference. Each memory is found to be associated with a nearly steady state of the dynamics which we refer to as a 'slow point'. Slow point speeds predict extrapolation performance across all datasets, protocols and architectures tested. Furthermore, by tracking the formation of the slow points we are able to understand the origin of differences between training protocols. Finally, we propose a novel regularization technique that is based on the relation between hidden state speeds and memory longevity. Our technique manipulates these speeds, thereby leading to a dramatic improvement in memory robustness over time, and could pave the way for a new class of regularization methods.