Omri Barak
Finding separatrices of dynamical flows with Deep Koopman Eigenfunctions
May 21, 2025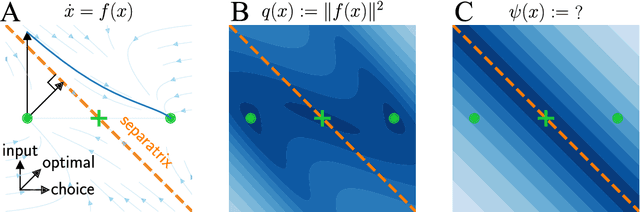
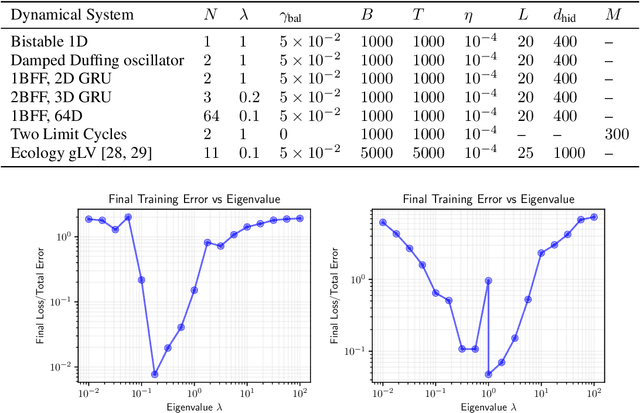
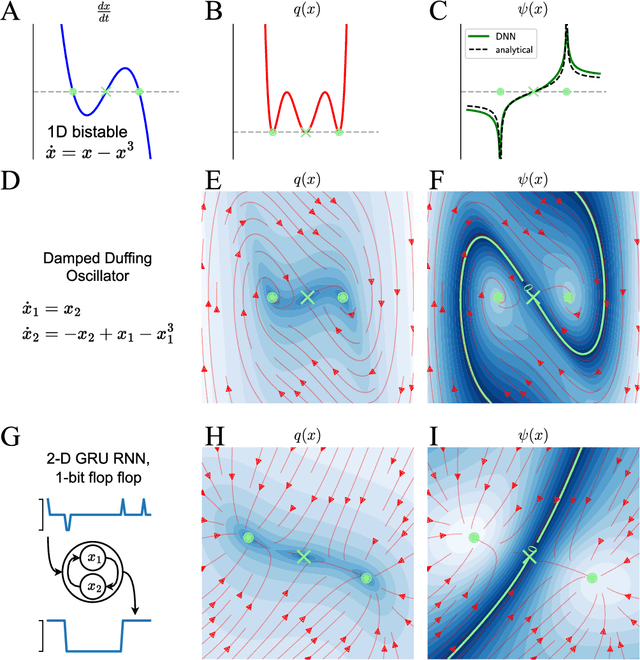
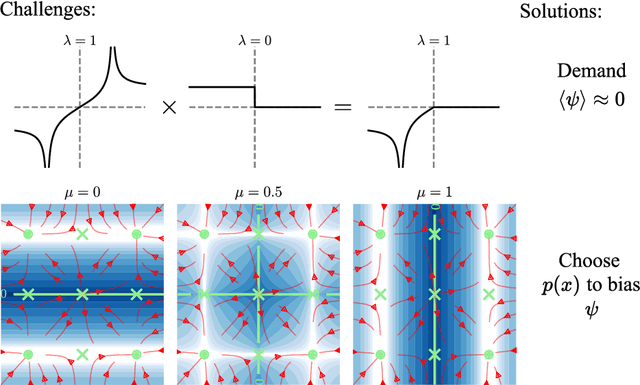
Abstract:Many natural systems, including neural circuits involved in decision making, can be modeled as high-dimensional dynamical systems with multiple stable states. While existing analytical tools primarily describe behavior near stable equilibria, characterizing separatrices -- the manifolds that delineate boundaries between different basins of attraction -- remains challenging, particularly in high-dimensional settings. Here, we introduce a numerical framework leveraging Koopman Theory combined with Deep Neural Networks to effectively characterize separatrices. Specifically, we approximate Koopman Eigenfunctions (KEFs) associated with real positive eigenvalues, which vanish precisely at the separatrices. Utilizing these scalar KEFs, optimization methods efficiently locate separatrices even in complex systems. We demonstrate our approach on synthetic benchmarks, ecological network models, and recurrent neural networks trained on neuroscience-inspired tasks. Moreover, we illustrate the practical utility of our method by designing optimal perturbations that can shift systems across separatrices, enabling predictions relevant to optogenetic stimulation experiments in neuroscience.
When predict can also explain: few-shot prediction to select better neural latents
May 23, 2024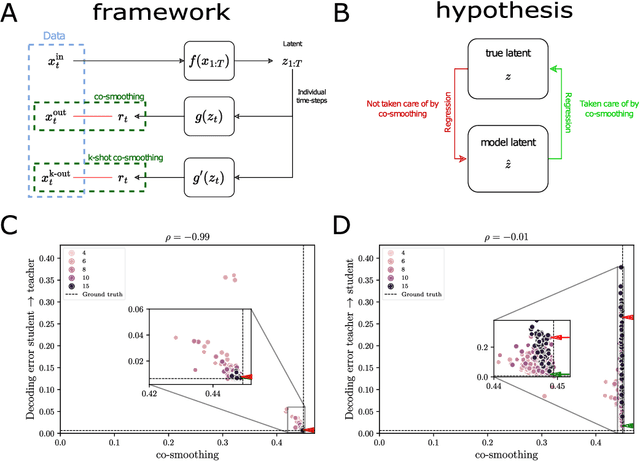
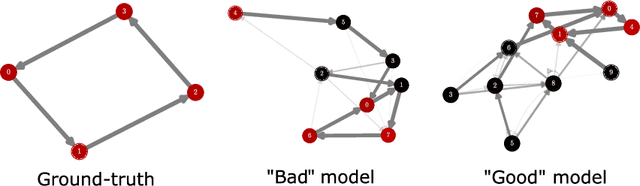
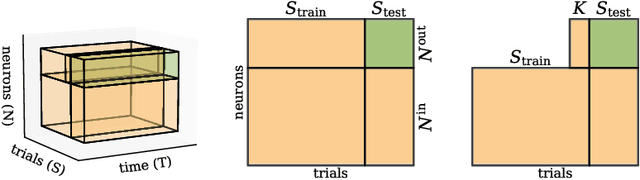
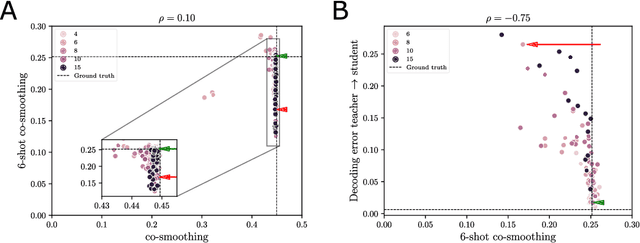
Abstract:Latent variable models serve as powerful tools to infer underlying dynamics from observed neural activity. However, due to the absence of ground truth data, prediction benchmarks are often employed as proxies. In this study, we reveal the limitations of the widely-used 'co-smoothing' prediction framework and propose an improved few-shot prediction approach that encourages more accurate latent dynamics. Utilizing a student-teacher setup with Hidden Markov Models, we demonstrate that the high co-smoothing model space can encompass models with arbitrary extraneous dynamics within their latent representations. To address this, we introduce a secondary metric -- a few-shot version of co-smoothing. This involves performing regression from the latent variables to held-out channels in the data using fewer trials. Our results indicate that among models with near-optimal co-smoothing, those with extraneous dynamics underperform in the few-shot co-smoothing compared to 'minimal' models devoid of such dynamics. We also provide analytical insights into the origin of this phenomenon. We further validate our findings on real neural data using two state-of-the-art methods: LFADS and STNDT. In the absence of ground truth, we suggest a proxy measure to quantify extraneous dynamics. By cross-decoding the latent variables of all model pairs with high co-smoothing, we identify models with minimal extraneous dynamics. We find a correlation between few-shot co-smoothing performance and this new measure. In summary, we present a novel prediction metric designed to yield latent variables that more accurately reflect the ground truth, offering a significant improvement for latent dynamics inference.
Repeated sequential learning increases memory capacity via effective decorrelation in a recurrent neural network
Jun 22, 2019



Abstract:Memories in neural system are shaped through the interplay of neural and learning dynamics under external inputs. By introducing a simple local learning rule to a neural network, we found that the memory capacity is drastically increased by sequentially repeating the learning steps of input-output mappings. The origin of this enhancement is attributed to the generation of a Psuedo-inverse correlation in the connectivity. This is associated with the emergence of spontaneous activity that intermittently exhibits neural patterns corresponding to embedded memories. Stablization of memories is achieved by a distinct bifurcation from the spontaneous activity under the application of each input.
Understanding and Controlling Memory in Recurrent Neural Networks
Feb 19, 2019



Abstract:To be effective in sequential data processing, Recurrent Neural Networks (RNNs) are required to keep track of past events by creating memories. While the relation between memories and the network's hidden state dynamics was established over the last decade, previous works in this direction were of a predominantly descriptive nature focusing mainly on locating the dynamical objects of interest. In particular, it remained unclear how dynamical observables affect the performance, how they form and whether they can be manipulated. Here, we utilize different training protocols, datasets and architectures to obtain a range of networks solving a delayed classification task with similar performance, alongside substantial differences in their ability to extrapolate for longer delays. We analyze the dynamics of the network's hidden state, and uncover the reasons for this difference. Each memory is found to be associated with a nearly steady state of the dynamics which we refer to as a 'slow point'. Slow point speeds predict extrapolation performance across all datasets, protocols and architectures tested. Furthermore, by tracking the formation of the slow points we are able to understand the origin of differences between training protocols. Finally, we propose a novel regularization technique that is based on the relation between hidden state speeds and memory longevity. Our technique manipulates these speeds, thereby leading to a dramatic improvement in memory robustness over time, and could pave the way for a new class of regularization methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge