Yahel Manor
The Ramanujan Machine: Automatically Generated Conjectures on Fundamental Constants
Aug 03, 2019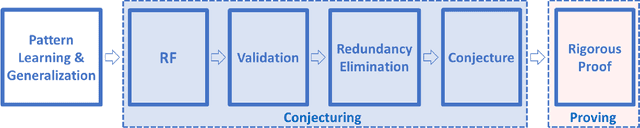



Abstract:Fundamental mathematical constants like $e$ and $\pi$ are ubiquitous in diverse fields of science, from abstract mathematics and geometry to physics, biology and chemistry. Nevertheless, for centuries new mathematical formulas relating fundamental constants have been scarce and usually discovered sporadically. In this paper we propose a novel and systematic approach that leverages algorithms for deriving mathematical formulas for fundamental constants and help reveal their underlying structure. Our algorithms find dozens of well-known as well as previously unknown continued fraction representations of $\pi$, $e$, and the Riemann zeta function values. Two conjectures produced by our algorithm, along with many others, are: \begin{equation*} \frac{e}{e-2} = 4 - \frac{1}{5-\frac{2}{6-\frac{3}{7-\frac{4}{8-\ldots}}}} \quad\quad,\quad\quad \frac{4}{3\pi-8} = 3-\frac{1\cdot1}{6-\frac{2\cdot3}{9-\frac{3\cdot5}{12-\frac{4\cdot 7}{15-\ldots}}}} \end{equation*} We present two algorithms that proved useful in finding conjectures: a variant of the Meet-In-The-Middle (MITM) algorithm and a Gradient Descent (GD) tailored to the recurrent structure of continued fractions. Both algorithms are based on matching numerical values and thus they conjecture formulas without providing proofs and without requiring any prior knowledge on any underlaying mathematical structure. This approach is especially attractive for fundamental constants for which no mathematical structure is known, as it reverses the conventional approach of sequential logic in formal proofs. Instead, our work supports a different conceptual approach for research: computer algorithms utilizing numerical data to unveil mathematical structures, thus trying to play the role of intuition of great mathematicians of the past, providing leads to new mathematical research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge