From Euler to AI: Unifying Formulas for Mathematical Constants

The constant $\pi$ has fascinated scholars for centuries, inspiring the derivation of countless formulas rooted in profound mathematical insight. This abundance of formulas raises a question: Are they interconnected, and can a unifying structure explain their relationships? We propose a systematic methodology for discovering and proving formula equivalences, leveraging modern large language models, large-scale data processing, and novel mathematical algorithms. Analyzing 457,145 arXiv papers, over a third of the validated formulas for $\pi$ were proven to be derivable from a single mathematical object - including formulas by Euler, Gauss, Lord Brouncker, and newer ones from algorithmic discoveries by the Ramanujan Machine. Our approach extends to other constants, such as $e$, $\zeta(3)$, and Catalan's constant, proving its broad applicability. This work represents a step toward the automatic unification of mathematical knowledge, laying a foundation for AI-driven discoveries of connections across scientific domains.

Algorithm-assisted discovery of an intrinsic order among mathematical constants

In recent decades, a growing number of discoveries in fields of mathematics have been assisted by computer algorithms, primarily for exploring large parameter spaces that humans would take too long to investigate. As computers and algorithms become more powerful, an intriguing possibility arises - the interplay between human intuition and computer algorithms can lead to discoveries of novel mathematical concepts that would otherwise remain elusive. To realize this perspective, we have developed a massively parallel computer algorithm that discovers an unprecedented number of continued fraction formulas for fundamental mathematical constants. The sheer number of formulas discovered by the algorithm unveils a novel mathematical structure that we call the conservative matrix field. Such matrix fields (1) unify thousands of existing formulas, (2) generate infinitely many new formulas, and most importantly, (3) lead to unexpected relations between different mathematical constants, including multiple integer values of the Riemann zeta function. Conservative matrix fields also enable new mathematical proofs of irrationality. In particular, we can use them to generalize the celebrated proof by Ap\'ery for the irrationality of $\zeta(3)$. Utilizing thousands of personal computers worldwide, our computer-supported research strategy demonstrates the power of experimental mathematics, highlighting the prospects of large-scale computational approaches to tackle longstanding open problems and discover unexpected connections across diverse fields of science.

The Ramanujan Machine: Automatically Generated Conjectures on Fundamental Constants

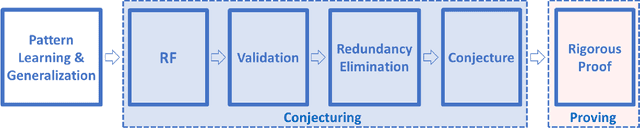
Fundamental mathematical constants like $e$ and $\pi$ are ubiquitous in diverse fields of science, from abstract mathematics and geometry to physics, biology and chemistry. Nevertheless, for centuries new mathematical formulas relating fundamental constants have been scarce and usually discovered sporadically. In this paper we propose a novel and systematic approach that leverages algorithms for deriving mathematical formulas for fundamental constants and help reveal their underlying structure. Our algorithms find dozens of well-known as well as previously unknown continued fraction representations of $\pi$, $e$, and the Riemann zeta function values. Two conjectures produced by our algorithm, along with many others, are: \begin{equation*} \frac{e}{e-2} = 4 - \frac{1}{5-\frac{2}{6-\frac{3}{7-\frac{4}{8-\ldots}}}} \quad\quad,\quad\quad \frac{4}{3\pi-8} = 3-\frac{1\cdot1}{6-\frac{2\cdot3}{9-\frac{3\cdot5}{12-\frac{4\cdot 7}{15-\ldots}}}} \end{equation*} We present two algorithms that proved useful in finding conjectures: a variant of the Meet-In-The-Middle (MITM) algorithm and a Gradient Descent (GD) tailored to the recurrent structure of continued fractions. Both algorithms are based on matching numerical values and thus they conjecture formulas without providing proofs and without requiring any prior knowledge on any underlaying mathematical structure. This approach is especially attractive for fundamental constants for which no mathematical structure is known, as it reverses the conventional approach of sequential logic in formal proofs. Instead, our work supports a different conceptual approach for research: computer algorithms utilizing numerical data to unveil mathematical structures, thus trying to play the role of intuition of great mathematicians of the past, providing leads to new mathematical research.