Algorithm-assisted discovery of an intrinsic order among mathematical constants

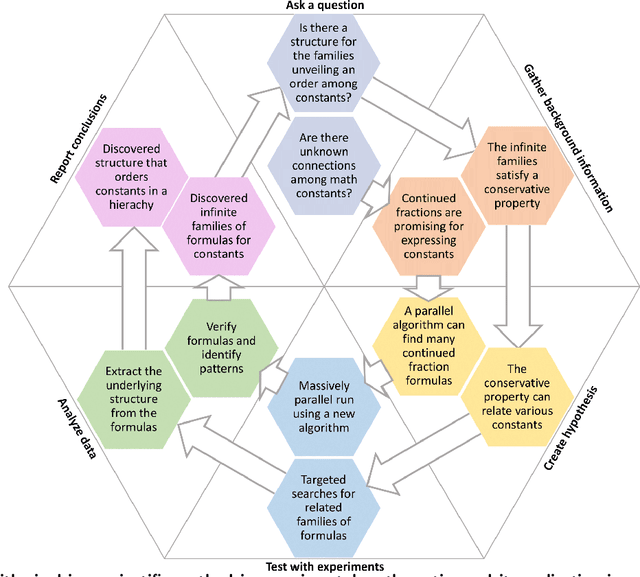
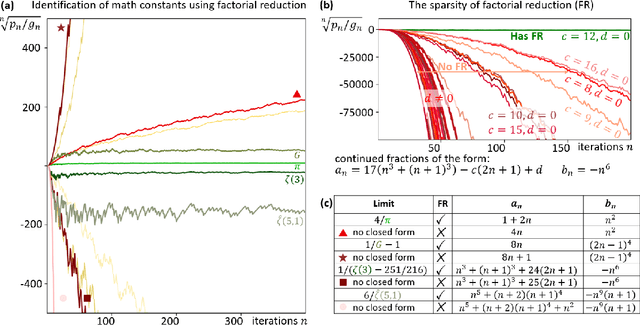
In recent decades, a growing number of discoveries in fields of mathematics have been assisted by computer algorithms, primarily for exploring large parameter spaces that humans would take too long to investigate. As computers and algorithms become more powerful, an intriguing possibility arises - the interplay between human intuition and computer algorithms can lead to discoveries of novel mathematical concepts that would otherwise remain elusive. To realize this perspective, we have developed a massively parallel computer algorithm that discovers an unprecedented number of continued fraction formulas for fundamental mathematical constants. The sheer number of formulas discovered by the algorithm unveils a novel mathematical structure that we call the conservative matrix field. Such matrix fields (1) unify thousands of existing formulas, (2) generate infinitely many new formulas, and most importantly, (3) lead to unexpected relations between different mathematical constants, including multiple integer values of the Riemann zeta function. Conservative matrix fields also enable new mathematical proofs of irrationality. In particular, we can use them to generalize the celebrated proof by Ap\'ery for the irrationality of $\zeta(3)$. Utilizing thousands of personal computers worldwide, our computer-supported research strategy demonstrates the power of experimental mathematics, highlighting the prospects of large-scale computational approaches to tackle longstanding open problems and discover unexpected connections across diverse fields of science.

A Computational Approach to Packet Classification

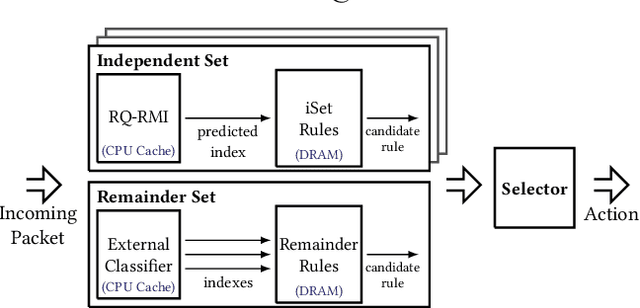
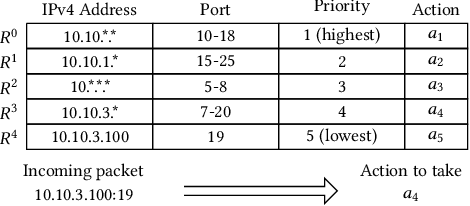
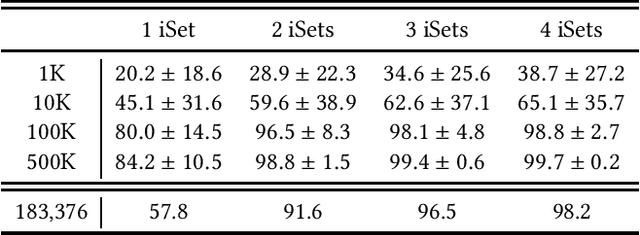
Multi-field packet classification is a crucial component in modern software-defined data center networks. To achieve high throughput and low latency, state-of-the-art algorithms strive to fit the rule lookup data structures into on-die caches; however, they do not scale well with the number of rules. We present a novel approach, NuevoMatch, which improves the memory scaling of existing methods. A new data structure, Range Query Recursive Model Index (RQ-RMI), is the key component that enables NuevoMatch to replace most of the accesses to main memory with model inference computations. We describe an efficient training algorithm which guarantees the correctness of the RQ-RMI-based classification. The use of RQ-RMI allows the packet rules to be compressed into model weights that fit into the hardware cache and takes advantage of the growing support for fast neural network processing in modern CPUs, such as wide vector processing engines, achieving a rate of tens of nanoseconds per lookup. Our evaluation using 500K multi-field rules from the standard ClassBench benchmark shows a geomean compression factor of 4.9X, 8X, and 82X, and an average performance improvement of 2.7X, 4.4X and 2.6X in latency and 1.3X, 2.2X, and 1.2X in throughput compared to CutSplit, NeuroCuts, and TupleMerge, all state-of-the-art algorithms.

Faster Neural Network Training with Approximate Tensor Operations

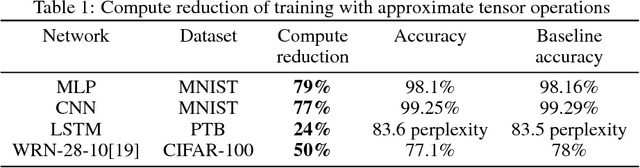
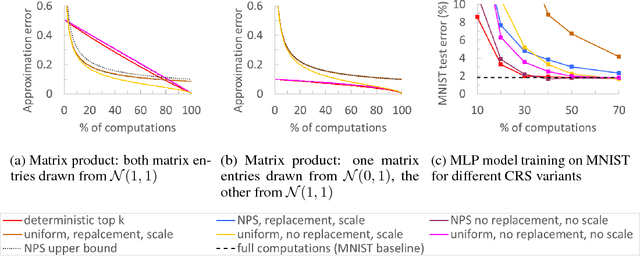
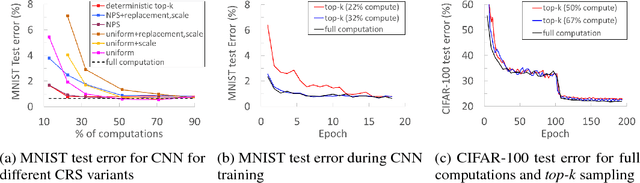
We propose a novel technique for faster Neural Network (NN) training by systematically approximating all the constituent matrix multiplications and convolutions. This approach is complementary to other approximation techniques, requires no changes to the dimensions of the network layers, hence compatible with existing training frameworks. We first analyze the applicability of the existing methods for approximating matrix multiplication to NN training, and extend the most suitable column-row sampling algorithm to approximating multi-channel convolutions. We apply approximate tensor operations to training MLP, CNN and LSTM network architectures on MNIST, CIFAR-100 and Penn Tree Bank datasets and demonstrate 30%-80% reduction in the amount of computations while maintaining little or no impact on the test accuracy. Our promising results encourage further study of general methods for approximating tensor operations and their application to NN training.