Faster Neural Network Training with Approximate Tensor Operations

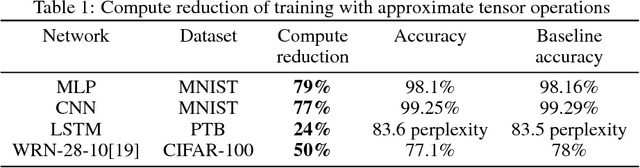
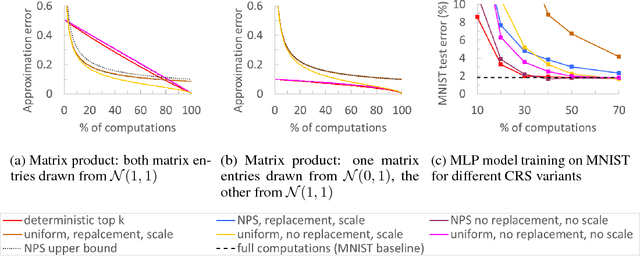
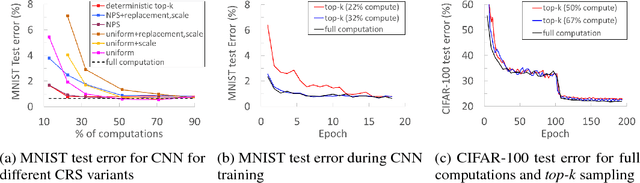
We propose a novel technique for faster Neural Network (NN) training by systematically approximating all the constituent matrix multiplications and convolutions. This approach is complementary to other approximation techniques, requires no changes to the dimensions of the network layers, hence compatible with existing training frameworks. We first analyze the applicability of the existing methods for approximating matrix multiplication to NN training, and extend the most suitable column-row sampling algorithm to approximating multi-channel convolutions. We apply approximate tensor operations to training MLP, CNN and LSTM network architectures on MNIST, CIFAR-100 and Penn Tree Bank datasets and demonstrate 30%-80% reduction in the amount of computations while maintaining little or no impact on the test accuracy. Our promising results encourage further study of general methods for approximating tensor operations and their application to NN training.