Efficient and Generic 1D Dilated Convolution Layer for Deep Learning

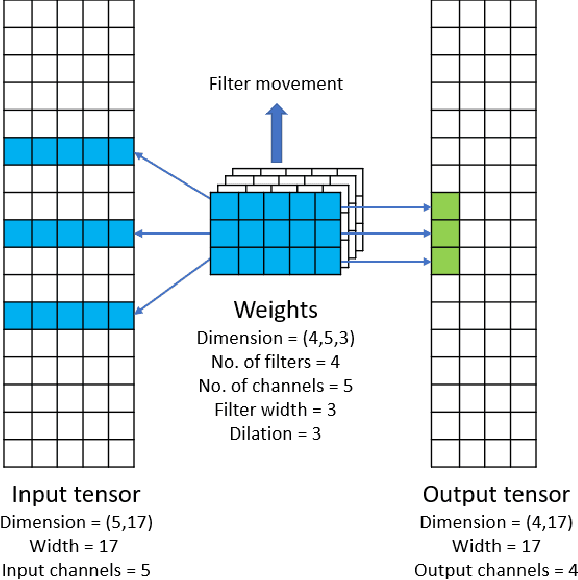
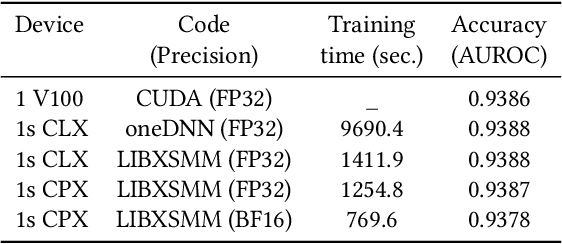
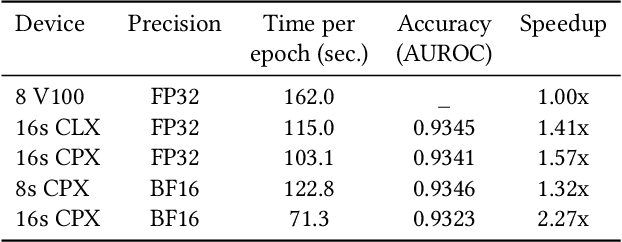
Convolutional neural networks (CNNs) have found many applications in tasks involving two-dimensional (2D) data, such as image classification and image processing. Therefore, 2D convolution layers have been heavily optimized on CPUs and GPUs. However, in many applications - for example genomics and speech recognition, the data can be one-dimensional (1D). Such applications can benefit from optimized 1D convolution layers. In this work, we introduce our efficient implementation of a generic 1D convolution layer covering a wide range of parameters. It is optimized for x86 CPU architectures, in particular, for architectures containing Intel AVX-512 and AVX-512 BFloat16 instructions. We use the LIBXSMM library's batch-reduce General Matrix Multiplication (BRGEMM) kernel for FP32 and BFloat16 precision. We demonstrate that our implementation can achieve up to 80% efficiency on Intel Xeon Cascade Lake and Cooper Lake CPUs. Additionally, we show the generalization capability of our BRGEMM based approach by achieving high efficiency across a range of parameters. We consistently achieve higher efficiency than the 1D convolution layer with Intel oneDNN library backend for varying input tensor widths, filter widths, number of channels, filters, and dilation parameters. Finally, we demonstrate the performance of our optimized 1D convolution layer by utilizing it in the end-to-end neural network training with real genomics datasets and achieve up to 6.86x speedup over the oneDNN library-based implementation on Cascade Lake CPUs. We also demonstrate the scaling with 16 sockets of Cascade/Cooper Lake CPUs and achieve significant speedup over eight V100 GPUs using a similar power envelop. In the end-to-end training, we get a speedup of 1.41x on Cascade Lake with FP32, 1.57x on Cooper Lake with FP32, and 2.27x on Cooper Lake with BFloat16 over eight V100 GPUs with FP32.

Tensor Processing Primitives: A Programming Abstraction for Efficiency and Portability in Deep Learning Workloads

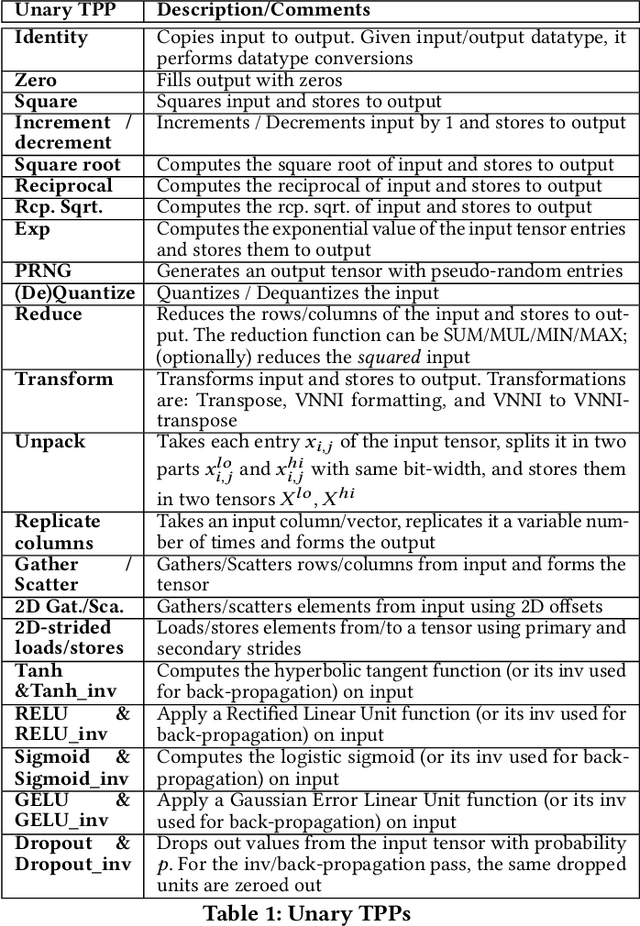
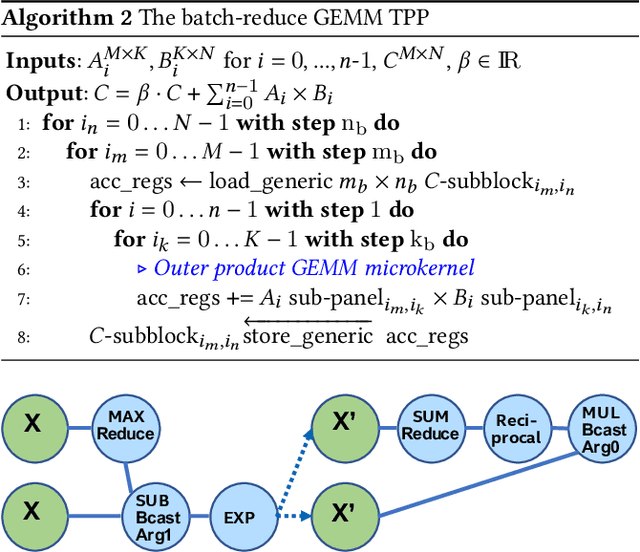
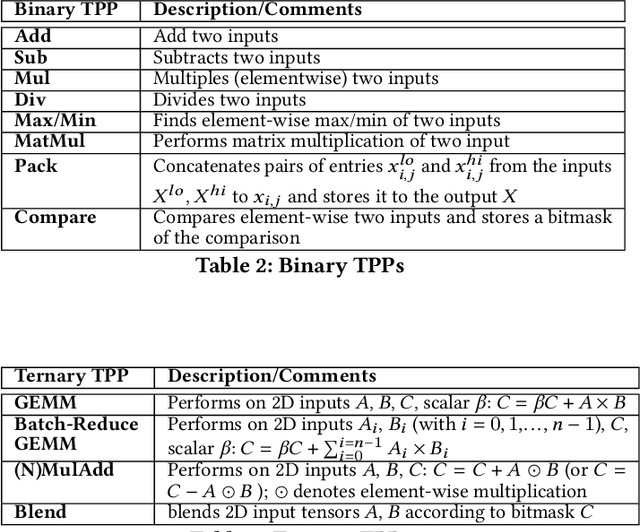
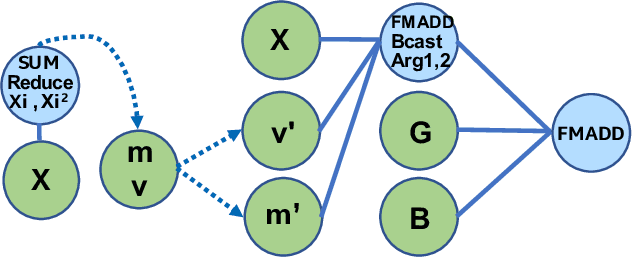
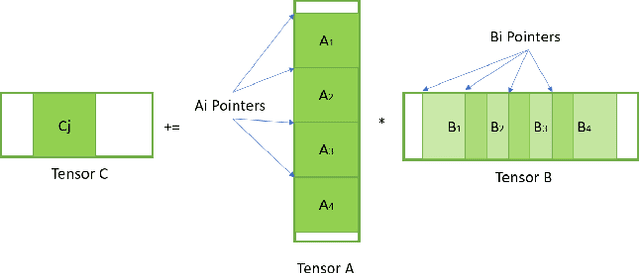
During the past decade, novel Deep Learning (DL) algorithms/workloads and hardware have been developed to tackle a wide range of problems. Despite the advances in workload/hardware ecosystems, the programming methodology of DL-systems is stagnant. DL-workloads leverage either highly-optimized, yet platform-specific and inflexible kernels from DL-libraries, or in the case of novel operators, reference implementations are built via DL-framework primitives with underwhelming performance. This work introduces the Tensor Processing Primitives (TPP), a programming abstraction striving for efficient, portable implementation of DL-workloads with high-productivity. TPPs define a compact, yet versatile set of 2D-tensor operators (or a virtual Tensor ISA), which subsequently can be utilized as building-blocks to construct complex operators on high-dimensional tensors. The TPP specification is platform-agnostic, thus code expressed via TPPs is portable, whereas the TPP implementation is highly-optimized and platform-specific. We demonstrate the efficacy of our approach using standalone kernels and end-to-end DL-workloads expressed entirely via TPPs that outperform state-of-the-art implementations on multiple platforms.

Faster Neural Network Training with Approximate Tensor Operations

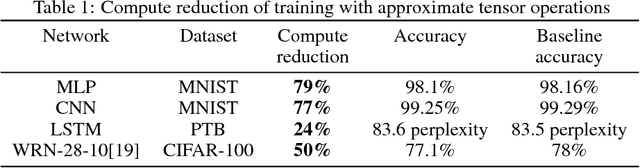
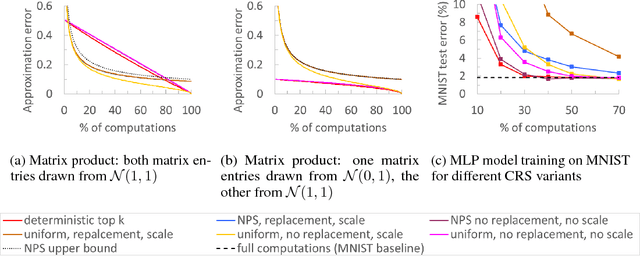
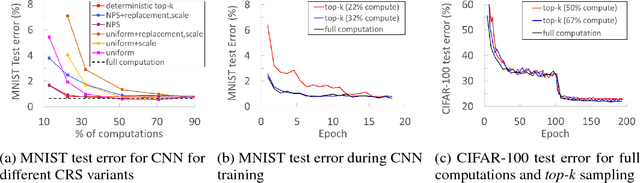
We propose a novel technique for faster Neural Network (NN) training by systematically approximating all the constituent matrix multiplications and convolutions. This approach is complementary to other approximation techniques, requires no changes to the dimensions of the network layers, hence compatible with existing training frameworks. We first analyze the applicability of the existing methods for approximating matrix multiplication to NN training, and extend the most suitable column-row sampling algorithm to approximating multi-channel convolutions. We apply approximate tensor operations to training MLP, CNN and LSTM network architectures on MNIST, CIFAR-100 and Penn Tree Bank datasets and demonstrate 30%-80% reduction in the amount of computations while maintaining little or no impact on the test accuracy. Our promising results encourage further study of general methods for approximating tensor operations and their application to NN training.