Abhisek Kundu
AUTOSPARSE: Towards Automated Sparse Training of Deep Neural Networks
Apr 14, 2023Abstract:Sparse training is emerging as a promising avenue for reducing the computational cost of training neural networks. Several recent studies have proposed pruning methods using learnable thresholds to efficiently explore the non-uniform distribution of sparsity inherent within the models. In this paper, we propose Gradient Annealing (GA), where gradients of masked weights are scaled down in a non-linear manner. GA provides an elegant trade-off between sparsity and accuracy without the need for additional sparsity-inducing regularization. We integrated GA with the latest learnable pruning methods to create an automated sparse training algorithm called AutoSparse, which achieves better accuracy and/or training/inference FLOPS reduction than existing learnable pruning methods for sparse ResNet50 and MobileNetV1 on ImageNet-1K: AutoSparse achieves (2x, 7x) reduction in (training,inference) FLOPS for ResNet50 on ImageNet at 80% sparsity. Finally, AutoSparse outperforms sparse-to-sparse SotA method MEST (uniform sparsity) for 80% sparse ResNet50 with similar accuracy, where MEST uses 12% more training FLOPS and 50% more inference FLOPS.
Tensor Processing Primitives: A Programming Abstraction for Efficiency and Portability in Deep Learning Workloads
Apr 14, 2021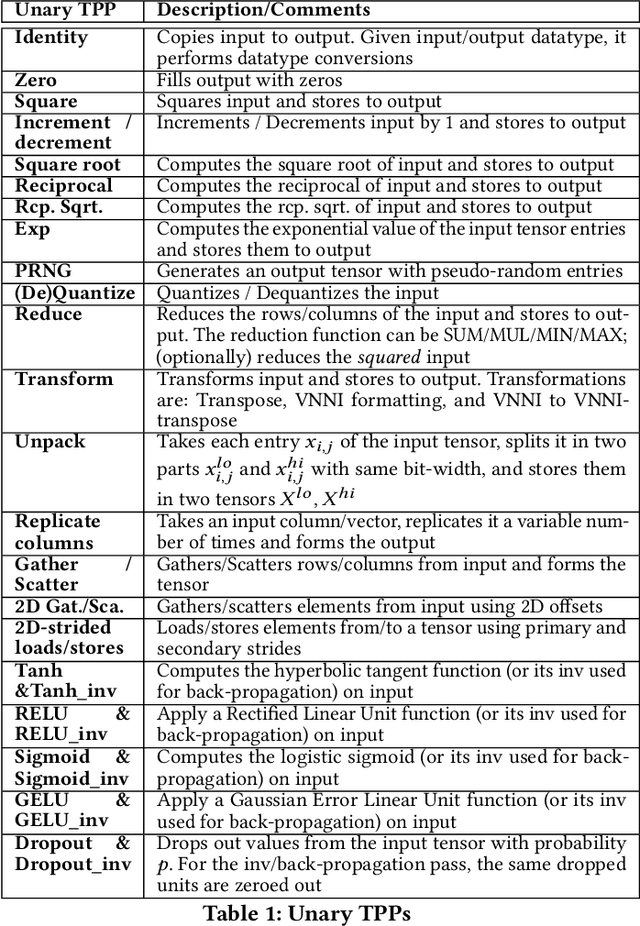
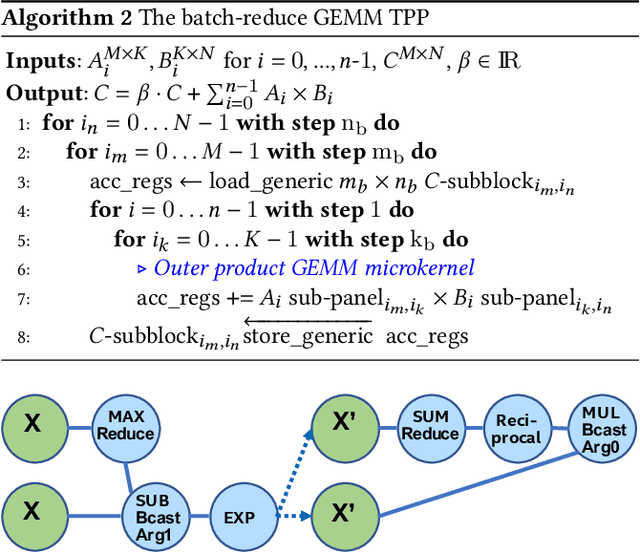
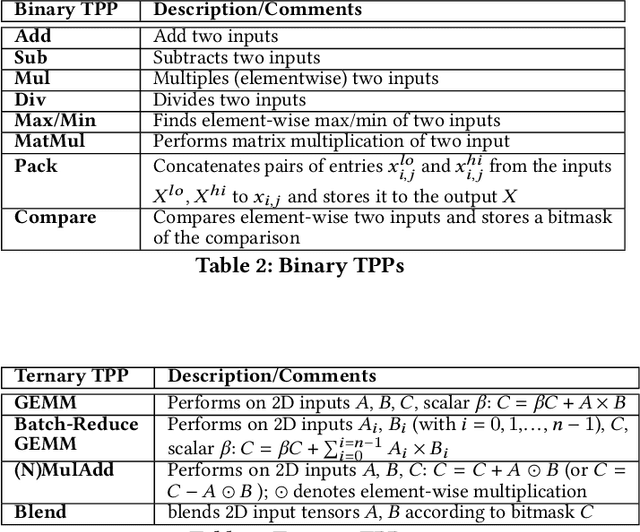
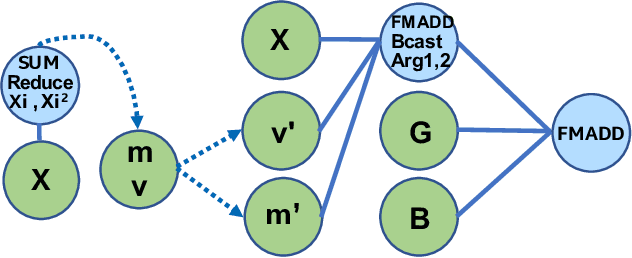
Abstract:During the past decade, novel Deep Learning (DL) algorithms/workloads and hardware have been developed to tackle a wide range of problems. Despite the advances in workload/hardware ecosystems, the programming methodology of DL-systems is stagnant. DL-workloads leverage either highly-optimized, yet platform-specific and inflexible kernels from DL-libraries, or in the case of novel operators, reference implementations are built via DL-framework primitives with underwhelming performance. This work introduces the Tensor Processing Primitives (TPP), a programming abstraction striving for efficient, portable implementation of DL-workloads with high-productivity. TPPs define a compact, yet versatile set of 2D-tensor operators (or a virtual Tensor ISA), which subsequently can be utilized as building-blocks to construct complex operators on high-dimensional tensors. The TPP specification is platform-agnostic, thus code expressed via TPPs is portable, whereas the TPP implementation is highly-optimized and platform-specific. We demonstrate the efficacy of our approach using standalone kernels and end-to-end DL-workloads expressed entirely via TPPs that outperform state-of-the-art implementations on multiple platforms.
K-TanH: Hardware Efficient Activations For Deep Learning
Oct 21, 2019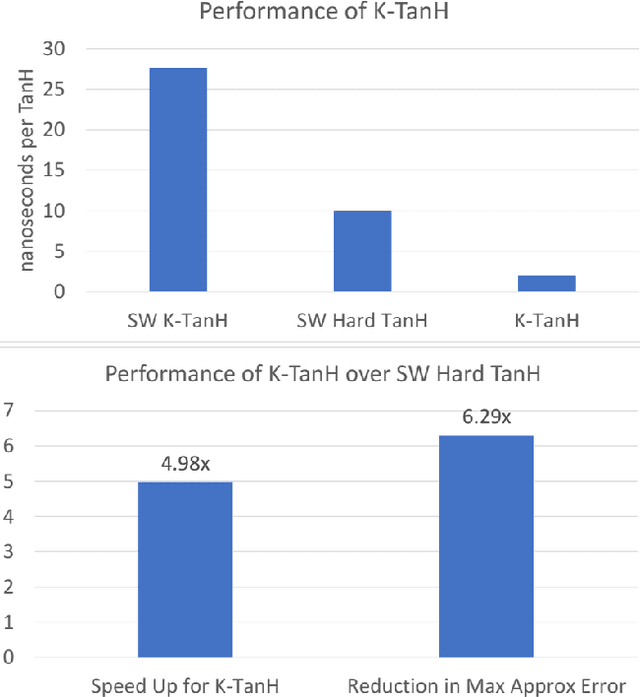
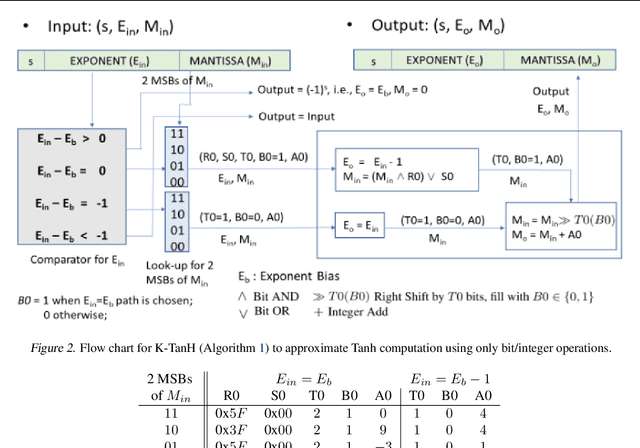

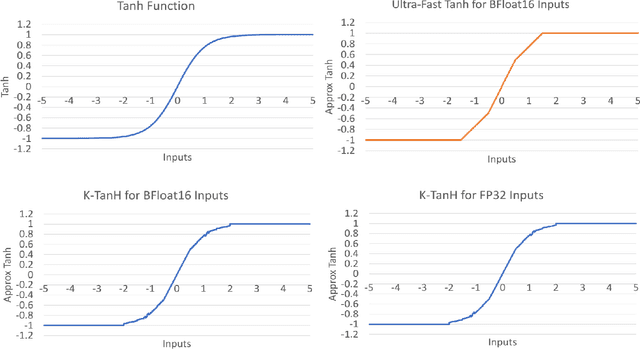
Abstract:We propose K-TanH, a novel, highly accurate, hardware efficient approximation of popular activation function Tanh for Deep Learning. K-TanH consists of a sequence of parameterized bit/integer operations, such as, masking, shift and add/subtract (no floating point operation needed) where parameters are stored in a very small look-up table (bit-masking step can be eliminated). The design of K-TanH is flexible enough to deal with multiple numerical formats, such as, FP32 and BFloat16. High quality approximations to other activation functions, e.g., Swish and GELU, can be derived from K-TanH. We provide RTL design for K-TanH to demonstrate its area/power/performance efficacy. It is more accurate than existing piecewise approximations for Tanh. For example, K-TanH achieves $\sim 5\times$ speed up and $> 6\times$ reduction in maximum approximation error over software implementation of Hard TanH. Experimental results for low-precision BFloat16 training of language translation model GNMT on WMT16 data sets with approximate Tanh and Sigmoid obtained via K-TanH achieve similar accuracy and convergence as training with exact Tanh and Sigmoid.
A Study of BFLOAT16 for Deep Learning Training
Jun 13, 2019



Abstract:This paper presents the first comprehensive empirical study demonstrating the efficacy of the Brain Floating Point (BFLOAT16) half-precision format for Deep Learning training across image classification, speech recognition, language modeling, generative networks and industrial recommendation systems. BFLOAT16 is attractive for Deep Learning training for two reasons: the range of values it can represent is the same as that of IEEE 754 floating-point format (FP32) and conversion to/from FP32 is simple. Maintaining the same range as FP32 is important to ensure that no hyper-parameter tuning is required for convergence; e.g., IEEE 754 compliant half-precision floating point (FP16) requires hyper-parameter tuning. In this paper, we discuss the flow of tensors and various key operations in mixed precision training, and delve into details of operations, such as the rounding modes for converting FP32 tensors to BFLOAT16. We have implemented a method to emulate BFLOAT16 operations in Tensorflow, Caffe2, IntelCaffe, and Neon for our experiments. Our results show that deep learning training using BFLOAT16 tensors achieves the same state-of-the-art (SOTA) results across domains as FP32 tensors in the same number of iterations and with no changes to hyper-parameters.
Ternary Residual Networks
Oct 31, 2017



Abstract:Sub-8-bit representation of DNNs incur some discernible loss of accuracy despite rigorous (re)training at low-precision. Such loss of accuracy essentially makes them equivalent to a much shallower counterpart, diminishing the power of being deep networks. To address this problem of accuracy drop we introduce the notion of \textit{residual networks} where we add more low-precision edges to sensitive branches of the sub-8-bit network to compensate for the lost accuracy. Further, we present a perturbation theory to identify such sensitive edges. Aided by such an elegant trade-off between accuracy and compute, the 8-2 model (8-bit activations, ternary weights), enhanced by ternary residual edges, turns out to be sophisticated enough to achieve very high accuracy ($\sim 1\%$ drop from our FP-32 baseline), despite $\sim 1.6\times$ reduction in model size, $\sim 26\times$ reduction in number of multiplications, and potentially $\sim 2\times$ power-performance gain comparing to 8-8 representation, on the state-of-the-art deep network ResNet-101 pre-trained on ImageNet dataset. Moreover, depending on the varying accuracy requirements in a dynamic environment, the deployed low-precision model can be upgraded/downgraded on-the-fly by partially enabling/disabling residual connections. For example, disabling the least important residual connections in the above enhanced network, the accuracy drop is $\sim 2\%$ (from FP32), despite $\sim 1.9\times$ reduction in model size, $\sim 32\times$ reduction in number of multiplications, and potentially $\sim 2.3\times$ power-performance gain comparing to 8-8 representation. Finally, all the ternary connections are sparse in nature, and the ternary residual conversion can be done in a resource-constraint setting with no low-precision (re)training.
Ternary Neural Networks with Fine-Grained Quantization
May 30, 2017
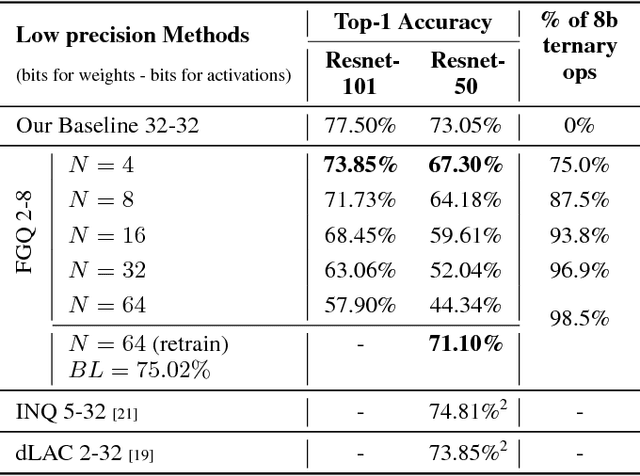


Abstract:We propose a novel fine-grained quantization (FGQ) method to ternarize pre-trained full precision models, while also constraining activations to 8 and 4-bits. Using this method, we demonstrate a minimal loss in classification accuracy on state-of-the-art topologies without additional training. We provide an improved theoretical formulation that forms the basis for a higher quality solution using FGQ. Our method involves ternarizing the original weight tensor in groups of $N$ weights. Using $N=4$, we achieve Top-1 accuracy within $3.7\%$ and $4.2\%$ of the baseline full precision result for Resnet-101 and Resnet-50 respectively, while eliminating $75\%$ of all multiplications. These results enable a full 8/4-bit inference pipeline, with best-reported accuracy using ternary weights on ImageNet dataset, with a potential of $9\times$ improvement in performance. Also, for smaller networks like AlexNet, FGQ achieves state-of-the-art results. We further study the impact of group size on both performance and accuracy. With a group size of $N=64$, we eliminate $\approx99\%$ of the multiplications; however, this introduces a noticeable drop in accuracy, which necessitates fine tuning the parameters at lower precision. We address this by fine-tuning Resnet-50 with 8-bit activations and ternary weights at $N=64$, improving the Top-1 accuracy to within $4\%$ of the full precision result with $<30\%$ additional training overhead. Our final quantized model can run on a full 8-bit compute pipeline using 2-bit weights and has the potential of up to $15\times$ improvement in performance compared to baseline full-precision models.
Mixed Low-precision Deep Learning Inference using Dynamic Fixed Point
Feb 01, 2017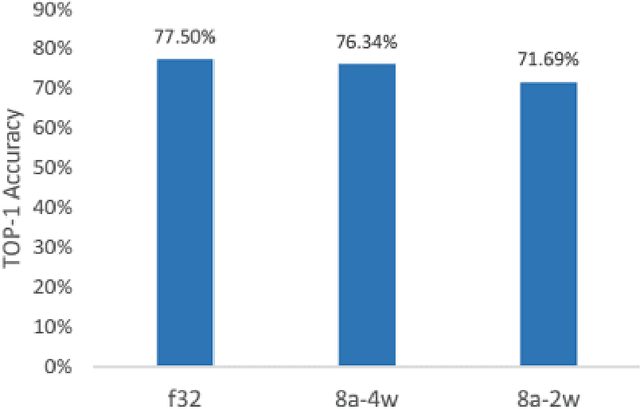

Abstract:We propose a cluster-based quantization method to convert pre-trained full precision weights into ternary weights with minimal impact on the accuracy. In addition, we also constrain the activations to 8-bits thus enabling sub 8-bit full integer inference pipeline. Our method uses smaller clusters of N filters with a common scaling factor to minimize the quantization loss, while also maximizing the number of ternary operations. We show that with a cluster size of N=4 on Resnet-101, can achieve 71.8% TOP-1 accuracy, within 6% of the best full precision results while replacing ~85% of all multiplications with 8-bit accumulations. Using the same method with 4-bit weights achieves 76.3% TOP-1 accuracy which within 2% of the full precision result. We also study the impact of the size of the cluster on both performance and accuracy, larger cluster sizes N=64 can replace ~98% of the multiplications with ternary operations but introduces significant drop in accuracy which necessitates fine tuning the parameters with retraining the network at lower precision. To address this we have also trained low-precision Resnet-50 with 8-bit activations and ternary weights by pre-initializing the network with full precision weights and achieve 68.9% TOP-1 accuracy within 4 additional epochs. Our final quantized model can run on a full 8-bit compute pipeline, with a potential 16x improvement in performance compared to baseline full-precision models.
A Randomized Rounding Algorithm for Sparse PCA
Nov 22, 2016


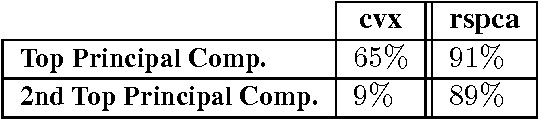
Abstract:We present and analyze a simple, two-step algorithm to approximate the optimal solution of the sparse PCA problem. Our approach first solves a L1 penalized version of the NP-hard sparse PCA optimization problem and then uses a randomized rounding strategy to sparsify the resulting dense solution. Our main theoretical result guarantees an additive error approximation and provides a tradeoff between sparsity and accuracy. Our experimental evaluation indicates that our approach is competitive in practice, even compared to state-of-the-art toolboxes such as Spasm.
Relaxed Leverage Sampling for Low-rank Matrix Completion
Apr 07, 2016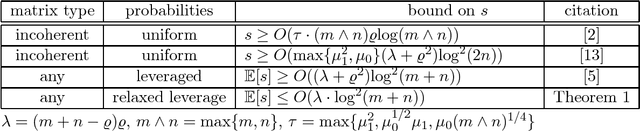
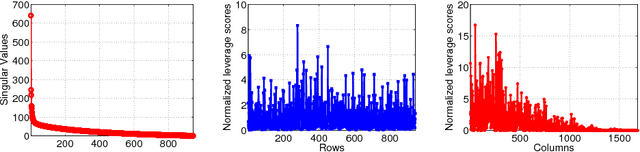

Abstract:We consider the problem of exact recovery of any $m\times n$ matrix of rank $\varrho$ from a small number of observed entries via the standard nuclear norm minimization framework. Such low-rank matrices have degrees of freedom $(m+n)\varrho - \varrho^2$. We show that any arbitrary low-rank matrices can be recovered exactly from a $\Theta\left(((m+n)\varrho - \varrho^2)\log^2(m+n)\right)$ randomly sampled entries, thus matching the lower bound on the required number of entries (in terms of degrees of freedom), with an additional factor of $O(\log^2(m+n))$. To achieve this bound on sample size we observe each entry with probabilities proportional to the sum of corresponding row and column leverage scores, minus their product. We show that this relaxation in sampling probabilities (as opposed to sum of leverage scores in Chen et al, 2014) can give us an $O(\varrho^2\log^2(m+n))$ additive improvement on the (best known) sample size obtained by Chen et al, 2014, for the nuclear norm minimization. Experiments on real data corroborate the theoretical improvement on sample size. Further, exact recovery of $(a)$ incoherent matrices (with restricted leverage scores), and $(b)$ matrices with only one of the row or column spaces to be incoherent, can be performed using our relaxed leverage score sampling, via nuclear norm minimization, without knowing the leverage scores a priori. In such settings also we can achieve improvement on sample size.
Approximating Sparse PCA from Incomplete Data
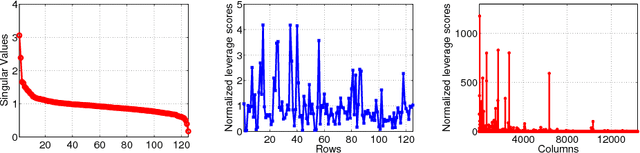
Mar 12, 2015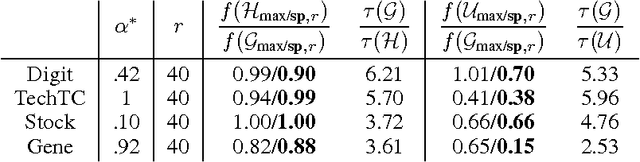



Abstract:We study how well one can recover sparse principal components of a data matrix using a sketch formed from a few of its elements. We show that for a wide class of optimization problems, if the sketch is close (in the spectral norm) to the original data matrix, then one can recover a near optimal solution to the optimization problem by using the sketch. In particular, we use this approach to obtain sparse principal components and show that for \math{m} data points in \math{n} dimensions, \math{O(\epsilon^{-2}\tilde k\max\{m,n\})} elements gives an \math{\epsilon}-additive approximation to the sparse PCA problem (\math{\tilde k} is the stable rank of the data matrix). We demonstrate our algorithms extensively on image, text, biological and financial data. The results show that not only are we able to recover the sparse PCAs from the incomplete data, but by using our sparse sketch, the running time drops by a factor of five or more.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge