Approximating Sparse PCA from Incomplete Data
Paper and Code
Mar 12, 2015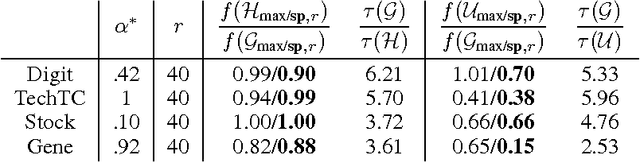



We study how well one can recover sparse principal components of a data matrix using a sketch formed from a few of its elements. We show that for a wide class of optimization problems, if the sketch is close (in the spectral norm) to the original data matrix, then one can recover a near optimal solution to the optimization problem by using the sketch. In particular, we use this approach to obtain sparse principal components and show that for \math{m} data points in \math{n} dimensions, \math{O(\epsilon^{-2}\tilde k\max\{m,n\})} elements gives an \math{\epsilon}-additive approximation to the sparse PCA problem (\math{\tilde k} is the stable rank of the data matrix). We demonstrate our algorithms extensively on image, text, biological and financial data. The results show that not only are we able to recover the sparse PCAs from the incomplete data, but by using our sparse sketch, the running time drops by a factor of five or more.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge