Consistent Causal Inference of Group Effects in Non-Targeted Trials with Finitely Many Effect Levels

A treatment may be appropriate for some group (the ``sick" group) on whom it has a positive effect, but it can also have a detrimental effect on subjects from another group (the ``healthy" group). In a non-targeted trial both sick and healthy subjects may be treated, producing heterogeneous effects within the treated group. Inferring the correct treatment effect on the sick population is then difficult, because the effects on the different groups get tangled. We propose an efficient nonparametric approach to estimating the group effects, called {\bf PCM} (pre-cluster and merge). We prove its asymptotic consistency in a general setting and show, on synthetic data, more than a 10x improvement in accuracy over existing state-of-the-art. Our approach applies more generally to consistent estimation of functions with a finite range.

Predicting Time Series of Networked Dynamical Systems without Knowing Topology

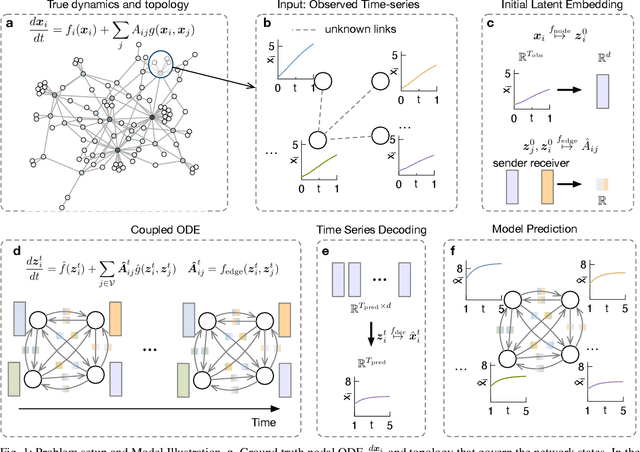
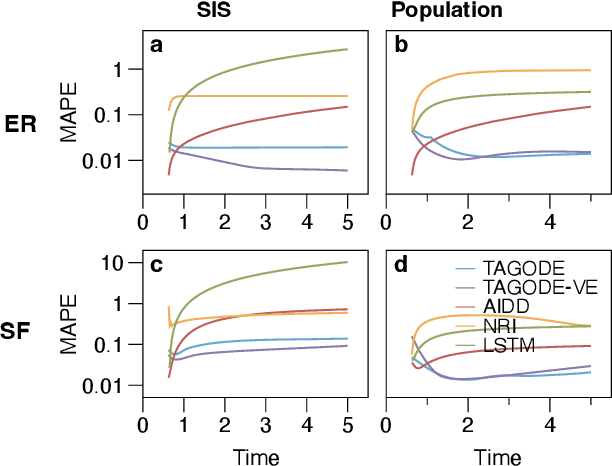
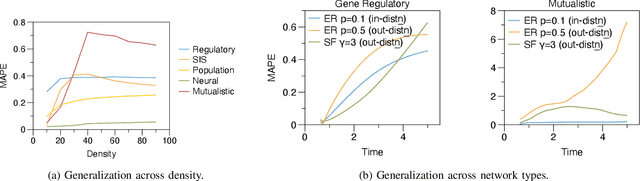
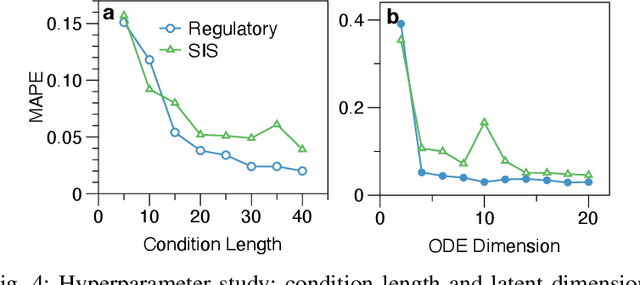
Many real-world complex systems, such as epidemic spreading networks and ecosystems, can be modeled as networked dynamical systems that produce multivariate time series. Learning the intrinsic dynamics from observational data is pivotal for forecasting system behaviors and making informed decisions. However, existing methods for modeling networked time series often assume known topologies, whereas real-world networks are typically incomplete or inaccurate, with missing or spurious links that hinder precise predictions. Moreover, while networked time series often originate from diverse topologies, the ability of models to generalize across topologies has not been systematically evaluated. To address these gaps, we propose a novel framework for learning network dynamics directly from observed time-series data, when prior knowledge of graph topology or governing dynamical equations is absent. Our approach leverages continuous graph neural networks with an attention mechanism to construct a latent topology, enabling accurate reconstruction of future trajectories for network states. Extensive experiments on real and synthetic networks demonstrate that our model not only captures dynamics effectively without topology knowledge but also generalizes to unseen time series originating from diverse topologies.

Privacy-Utility Tradeoff of OLS with Random Projections

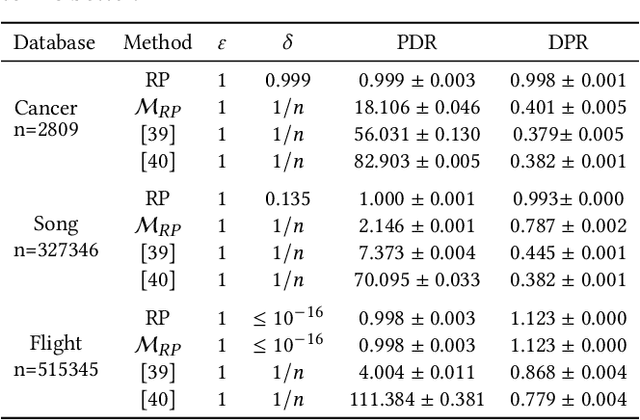
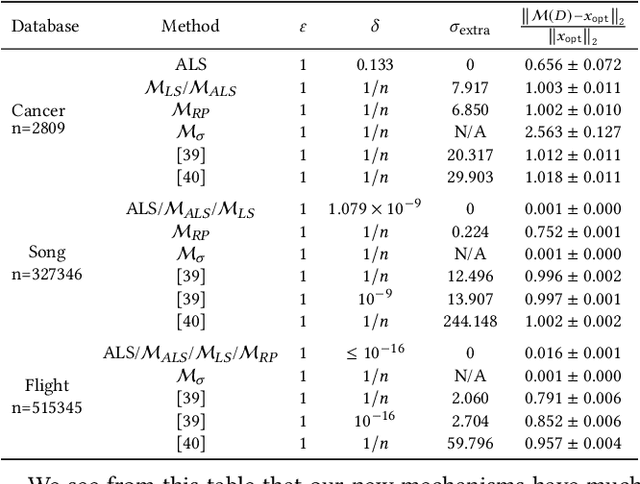
We study the differential privacy (DP) of a core ML problem, linear ordinary least squares (OLS), a.k.a. $\ell_2$-regression. Our key result is that the approximate LS algorithm (ALS) (Sarlos, 2006), a randomized solution to the OLS problem primarily used to improve performance on large datasets, also preserves privacy. ALS achieves a better privacy/utility tradeoff, without modifications or further noising, when compared to alternative private OLS algorithms which modify and/or noise OLS. We give the first {\em tight} DP-analysis for the ALS algorithm and the standard Gaussian mechanism (Dwork et al., 2014) applied to OLS. Our methodology directly improves the privacy analysis of (Blocki et al., 2012) and (Sheffet, 2019)) and introduces new tools which may be of independent interest: (1) the exact spectrum of $(\epsilon, \delta)$-DP parameters (``DP spectrum") for mechanisms whose output is a $d$-dimensional Gaussian, and (2) an improved DP spectrum for random projection (compared to (Blocki et al., 2012) and (Sheffet, 2019)). All methods for private OLS (including ours) assume, often implicitly, restrictions on the input database, such as bounds on leverage and residuals. We prove that such restrictions are necessary. Hence, computing the privacy of mechanisms such as ALS must estimate these database parameters, which can be infeasible in big datasets. For more complex ML models, DP bounds may not even be tractable. There is a need for blackbox DP-estimators (Lu et al., 2022) which empirically estimate a data-dependent privacy. We demonstrate the effectiveness of such a DP-estimator by empirically recovering a DP-spectrum that matches our theory for OLS. This validates the DP-estimator in a nontrivial ML application, opening the door to its use in more complex nonlinear ML settings where theory is unavailable.

Reduced Label Complexity For Tight $\ell_2$ Regression

Given data ${\rm X}\in\mathbb{R}^{n\times d}$ and labels $\mathbf{y}\in\mathbb{R}^{n}$ the goal is find $\mathbf{w}\in\mathbb{R}^d$ to minimize $\Vert{\rm X}\mathbf{w}-\mathbf{y}\Vert^2$. We give a polynomial algorithm that, \emph{oblivious to $\mathbf{y}$}, throws out $n/(d+\sqrt{n})$ data points and is a $(1+d/n)$-approximation to optimal in expectation. The motivation is tight approximation with reduced label complexity (number of labels revealed). We reduce label complexity by $\Omega(\sqrt{n})$. Open question: Can label complexity be reduced by $\Omega(n)$ with tight $(1+d/n)$-approximation?

Learning GraphQL Query Costs (Extended Version)

GraphQL is a query language for APIs and a runtime for executing those queries, fetching the requested data from existing microservices, REST APIs, databases, or other sources. Its expressiveness and its flexibility have made it an attractive candidate for API providers in many industries, especially through the web. A major drawback to blindly servicing a client's query in GraphQL is that the cost of a query can be unexpectedly large, creating computation and resource overload for the provider, and API rate-limit overages and infrastructure overload for the client. To mitigate these drawbacks, it is necessary to efficiently estimate the cost of a query before executing it. Estimating query cost is challenging, because GraphQL queries have a nested structure, GraphQL APIs follow different design conventions, and the underlying data sources are hidden. Estimates based on worst-case static query analysis have had limited success because they tend to grossly overestimate cost. We propose a machine-learning approach to efficiently and accurately estimate the query cost. We also demonstrate the power of this approach by testing it on query-response data from publicly available commercial APIs. Our framework is efficient and predicts query costs with high accuracy, consistently outperforming the static analysis by a large margin.

NoisyCUR: An algorithm for two-cost budgeted matrix completion

Matrix completion is a ubiquitous tool in machine learning and data analysis. Most work in this area has focused on the number of observations necessary to obtain an accurate low-rank approximation. In practice, however, the cost of observations is an important limiting factor, and experimentalists may have on hand multiple modes of observation with differing noise-vs-cost trade-offs. This paper considers matrix completion subject to such constraints: a budget is imposed and the experimentalist's goal is to allocate this budget between two sampling modalities in order to recover an accurate low-rank approximation. Specifically, we consider that it is possible to obtain low noise, high cost observations of individual entries or high noise, low cost observations of entire columns. We introduce a regression-based completion algorithm for this setting and experimentally verify the performance of our approach on both synthetic and real data sets. When the budget is low, our algorithm outperforms standard completion algorithms. When the budget is high, our algorithm has comparable error to standard nuclear norm completion algorithms and requires much less computational effort.

Training Deep Neural Networks with Constrained Learning Parameters

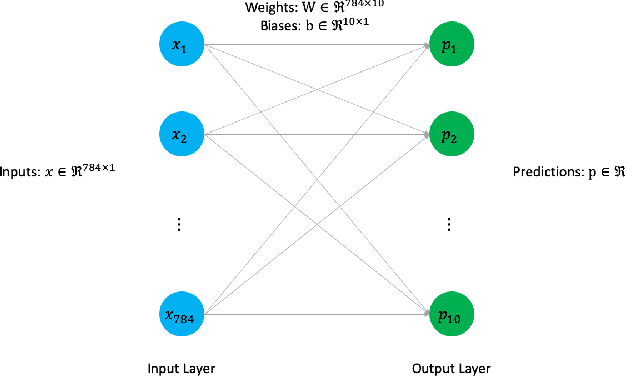
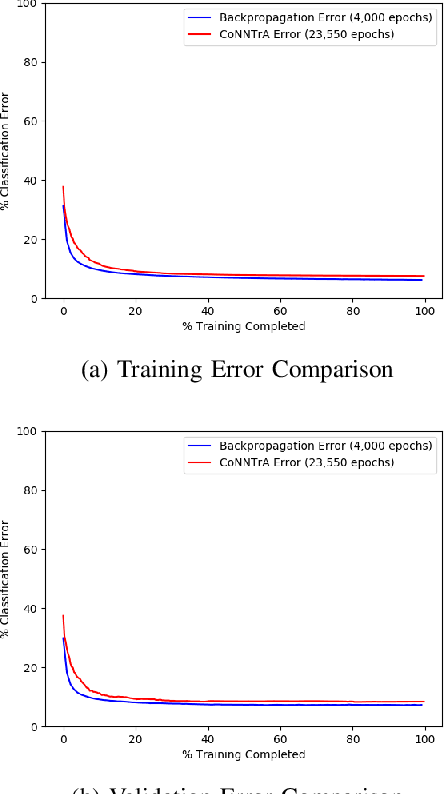
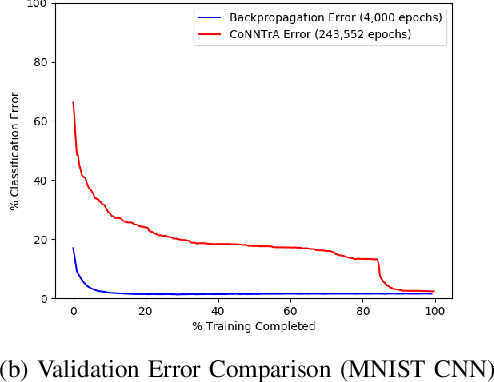
Today's deep learning models are primarily trained on CPUs and GPUs. Although these models tend to have low error, they consume high power and utilize large amount of memory owing to double precision floating point learning parameters. Beyond the Moore's law, a significant portion of deep learning tasks would run on edge computing systems, which will form an indispensable part of the entire computation fabric. Subsequently, training deep learning models for such systems will have to be tailored and adopted to generate models that have the following desirable characteristics: low error, low memory, and low power. We believe that deep neural networks (DNNs), where learning parameters are constrained to have a set of finite discrete values, running on neuromorphic computing systems would be instrumental for intelligent edge computing systems having these desirable characteristics. To this extent, we propose the Combinatorial Neural Network Training Algorithm (CoNNTrA), that leverages a coordinate gradient descent-based approach for training deep learning models with finite discrete learning parameters. Next, we elaborate on the theoretical underpinnings and evaluate the computational complexity of CoNNTrA. As a proof of concept, we use CoNNTrA to train deep learning models with ternary learning parameters on the MNIST, Iris and ImageNet data sets and compare their performance to the same models trained using Backpropagation. We use following performance metrics for the comparison: (i) Training error; (ii) Validation error; (iii) Memory usage; and (iv) Training time. Our results indicate that CoNNTrA models use 32x less memory and have errors at par with the Backpropagation models.

A New Mathematical Model for Controlled Pandemics Like COVID-19 : AI Implemented Predictions

We present a new mathematical model to explicitly capture the effects that the three restriction measures: the lockdown date and duration, social distancing and masks, and, schools and border closing, have in controlling the spread of COVID-19 infections $i(r, t)$. Before restrictions were introduced, the random spread of infections as described by the SEIR model grew exponentially. The addition of control measures introduces a mixing of order and disorder in the system's evolution which fall under a different mathematical class of models that can eventually lead to critical phenomena. A generic analytical solution is hard to obtain. We use machine learning to solve the new equations for $i(r,t)$, the infections $i$ in any region $r$ at time $t$ and derive predictions for the spread of infections over time as a function of the strength of the specific measure taken and their duration. The machine is trained in all of the COVID-19 published data for each region, county, state, and country in the world. It utilizes optimization to learn the best-fit values of the model's parameters from past data in each region in the world, and it updates the predicted infections curves for any future restrictions that may be added or relaxed anywhere. We hope this interdisciplinary effort, a new mathematical model that predicts the impact of each measure in slowing down infection spread combined with the solving power of machine learning, is a useful tool in the fight against the current pandemic and potentially future ones.

Machine Learning the Phenomenology of COVID-19 From Early Infection Dynamics

We present a robust data-driven machine learning analysis of the COVID-19 pandemic from its early infection dynamics, specifically infection counts over time. The goal is to extract actionable public health insights. These insights include the infectious force, the rate of a mild infection becoming serious, estimates for asymtomatic infections and predictions of new infections over time. We focus on USA data starting from the first confirmed infection on January 20 2020. Our methods reveal significant asymptomatic (hidden) infection, a lag of about 10 days, and we quantitatively confirm that the infectious force is strong with about a 0.14% transition from mild to serious infection. Our methods are efficient, robust and general, being agnostic to the specific virus and applicable to different populations or cohorts.

Fast Fixed Dimension L2-Subspace Embeddings of Arbitrary Accuracy, With Application to L1 and L2 Tasks

We give a fast oblivious L2-embedding of $A\in \mathbb{R}^{n x d}$ to $B\in \mathbb{R}^{r x d}$ satisfying $(1-\varepsilon)\|A x\|_2^2 \le \|B x\|_2^2 <= (1+\varepsilon) \|Ax\|_2^2.$ Our embedding dimension $r$ equals $d$, a constant independent of the distortion $\varepsilon$. We use as a black-box any L2-embedding $\Pi^T A$ and inherit its runtime and accuracy, effectively decoupling the dimension $r$ from runtime and accuracy, allowing downstream machine learning applications to benefit from both a low dimension and high accuracy (in prior embeddings higher accuracy means higher dimension). We give applications of our L2-embedding to regression, PCA and statistical leverage scores. We also give applications to L1: 1.) An oblivious L1-embedding with dimension $d+O(d\ln^{1+\eta} d)$ and distortion $O((d\ln d)/\ln\ln d)$, with application to constructing well-conditioned bases; 2.) Fast approximation of L1-Lewis weights using our L2 embedding to quickly approximate L2-leverage scores.