Gradient Flow Matching for Learning Update Dynamics in Neural Network Training

Training deep neural networks remains computationally intensive due to the itera2 tive nature of gradient-based optimization. We propose Gradient Flow Matching (GFM), a continuous-time modeling framework that treats neural network training as a dynamical system governed by learned optimizer-aware vector fields. By leveraging conditional flow matching, GFM captures the underlying update rules of optimizers such as SGD, Adam, and RMSprop, enabling smooth extrapolation of weight trajectories toward convergence. Unlike black-box sequence models, GFM incorporates structural knowledge of gradient-based updates into the learning objective, facilitating accurate forecasting of final weights from partial training sequences. Empirically, GFM achieves forecasting accuracy that is competitive with Transformer-based models and significantly outperforms LSTM and other classical baselines. Furthermore, GFM generalizes across neural architectures and initializations, providing a unified framework for studying optimization dynamics and accelerating convergence prediction.

Less is More: Efficient Weight Farcasting with 1-Layer Neural Network

Addressing the computational challenges inherent in training large-scale deep neural networks remains a critical endeavor in contemporary machine learning research. While previous efforts have focused on enhancing training efficiency through techniques such as gradient descent with momentum, learning rate scheduling, and weight regularization, the demand for further innovation continues to burgeon as model sizes keep expanding. In this study, we introduce a novel framework which diverges from conventional approaches by leveraging long-term time series forecasting techniques. Our method capitalizes solely on initial and final weight values, offering a streamlined alternative for complex model architectures. We also introduce a novel regularizer that is tailored to enhance the forecasting performance of our approach. Empirical evaluations conducted on synthetic weight sequences and real-world deep learning architectures, including the prominent large language model DistilBERT, demonstrate the superiority of our method in terms of forecasting accuracy and computational efficiency. Notably, our framework showcases improved performance while requiring minimal additional computational overhead, thus presenting a promising avenue for accelerating the training process across diverse tasks and architectures.

Inferring from Logits: Exploring Best Practices for Decoding-Free Generative Candidate Selection

Generative Language Models rely on autoregressive decoding to produce the output sequence token by token. Many tasks such as preference optimization, require the model to produce task-level output consisting of multiple tokens directly by selecting candidates from a pool as predictions. Determining a task-level prediction from candidates using the ordinary token-level decoding mechanism is constrained by time-consuming decoding and interrupted gradients by discrete token selection. Existing works have been using decoding-free candidate selection methods to obtain candidate probability from initial output logits over vocabulary. Though these estimation methods are widely used, they are not systematically evaluated, especially on end tasks. We introduce an evaluation of a comprehensive collection of decoding-free candidate selection approaches on a comprehensive set of tasks, including five multiple-choice QA tasks with a small candidate pool and four clinical decision tasks with a massive amount of candidates, some with 10k+ options. We evaluate the estimation methods paired with a wide spectrum of foundation LMs covering different architectures, sizes and training paradigms. The results and insights from our analysis inform the future model design.

Predicting Time Series of Networked Dynamical Systems without Knowing Topology

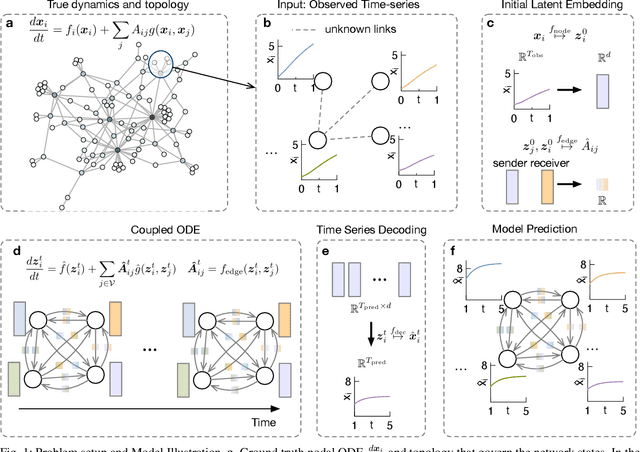
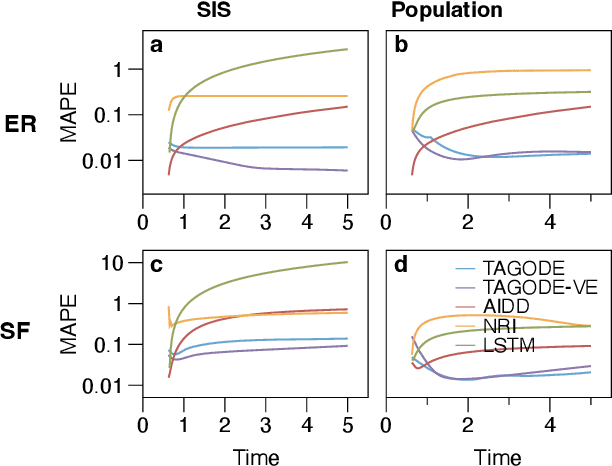
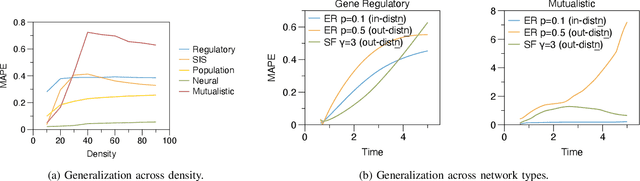
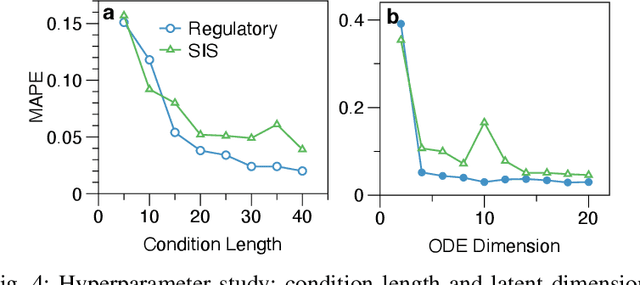
Many real-world complex systems, such as epidemic spreading networks and ecosystems, can be modeled as networked dynamical systems that produce multivariate time series. Learning the intrinsic dynamics from observational data is pivotal for forecasting system behaviors and making informed decisions. However, existing methods for modeling networked time series often assume known topologies, whereas real-world networks are typically incomplete or inaccurate, with missing or spurious links that hinder precise predictions. Moreover, while networked time series often originate from diverse topologies, the ability of models to generalize across topologies has not been systematically evaluated. To address these gaps, we propose a novel framework for learning network dynamics directly from observed time-series data, when prior knowledge of graph topology or governing dynamical equations is absent. Our approach leverages continuous graph neural networks with an attention mechanism to construct a latent topology, enabling accurate reconstruction of future trajectories for network states. Extensive experiments on real and synthetic networks demonstrate that our model not only captures dynamics effectively without topology knowledge but also generalizes to unseen time series originating from diverse topologies.

Architecture-Aware Learning Curve Extrapolation via Graph Ordinary Differential Equation

Learning curve extrapolation predicts neural network performance from early training epochs and has been applied to accelerate AutoML, facilitating hyperparameter tuning and neural architecture search. However, existing methods typically model the evolution of learning curves in isolation, neglecting the impact of neural network (NN) architectures, which influence the loss landscape and learning trajectories. In this work, we explore whether incorporating neural network architecture improves learning curve modeling and how to effectively integrate this architectural information. Motivated by the dynamical system view of optimization, we propose a novel architecture-aware neural differential equation model to forecast learning curves continuously. We empirically demonstrate its ability to capture the general trend of fluctuating learning curves while quantifying uncertainty through variational parameters. Our model outperforms current state-of-the-art learning curve extrapolation methods and pure time-series modeling approaches for both MLP and CNN-based learning curves. Additionally, we explore the applicability of our method in Neural Architecture Search scenarios, such as training configuration ranking.