Trustworthy Reputation Games and Applications to Proof-of-Reputation Blockchains

Reputation systems play an essential role in the Internet era, as they enable people to decide whom to trust, by collecting and aggregating data about users' behavior. Recently, several works proposed the use of reputation for the design and scalability improvement of decentralized (blockchain) ledgers; however, such systems are prone to manipulation and to our knowledge no game-theoretic treatment exists that can support their economic robustness. In this work we put forth a new model for the design of what we call, {\em trustworthy reputation systems}. Concretely, we describe a class of games, which we term {\em trustworthy reputation games}, that enable a set of users to report a function of their beliefs about the trustworthiness of each server in a set -- i.e., their estimate of the probability that this server will behave according to its specified strategy -- in a way that satisfies the following properties: 1. It is $(\epsilon$-)best response for any rational user in the game to play a prescribed (truthful) strategy according to their true belief. 2. Assuming that the users' beliefs are not too far from the {\em true} trustworthiness of the servers, playing the above ($\epsilon-$)Nash equilibrium allows anyone who observes the users' strategies to estimate the relative trustworthiness of any two servers. Our utilities and decoding function build on a connection between the well known PageRank algorithm and the problem of trustworthiness discovery, which can be of independent interest. Finally, we show how the above games are motivated by and can be leveraged in proof-of-reputation (PoR) blockchains.

Privacy-Utility Tradeoff of OLS with Random Projections

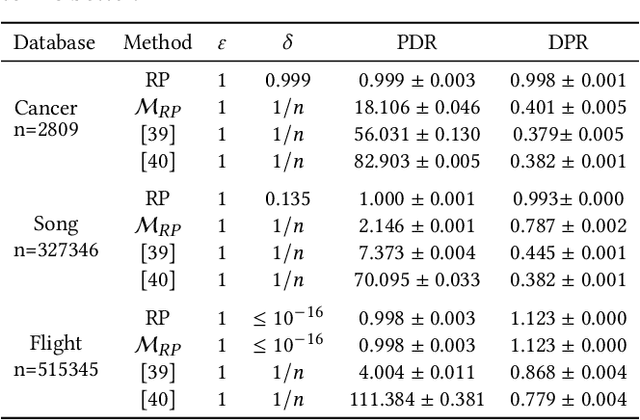
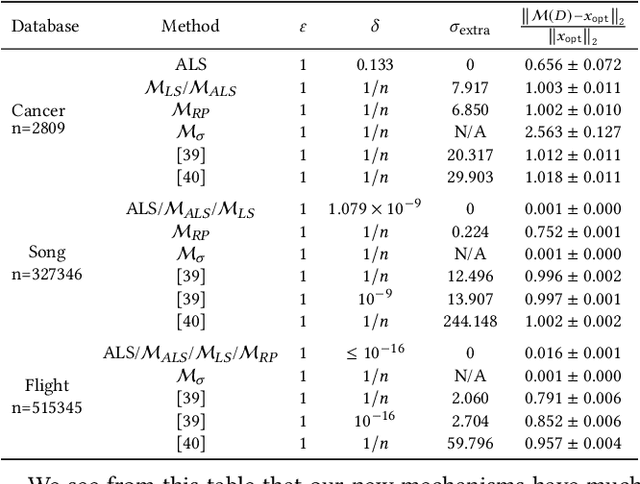
We study the differential privacy (DP) of a core ML problem, linear ordinary least squares (OLS), a.k.a. $\ell_2$-regression. Our key result is that the approximate LS algorithm (ALS) (Sarlos, 2006), a randomized solution to the OLS problem primarily used to improve performance on large datasets, also preserves privacy. ALS achieves a better privacy/utility tradeoff, without modifications or further noising, when compared to alternative private OLS algorithms which modify and/or noise OLS. We give the first {\em tight} DP-analysis for the ALS algorithm and the standard Gaussian mechanism (Dwork et al., 2014) applied to OLS. Our methodology directly improves the privacy analysis of (Blocki et al., 2012) and (Sheffet, 2019)) and introduces new tools which may be of independent interest: (1) the exact spectrum of $(\epsilon, \delta)$-DP parameters (``DP spectrum") for mechanisms whose output is a $d$-dimensional Gaussian, and (2) an improved DP spectrum for random projection (compared to (Blocki et al., 2012) and (Sheffet, 2019)). All methods for private OLS (including ours) assume, often implicitly, restrictions on the input database, such as bounds on leverage and residuals. We prove that such restrictions are necessary. Hence, computing the privacy of mechanisms such as ALS must estimate these database parameters, which can be infeasible in big datasets. For more complex ML models, DP bounds may not even be tractable. There is a need for blackbox DP-estimators (Lu et al., 2022) which empirically estimate a data-dependent privacy. We demonstrate the effectiveness of such a DP-estimator by empirically recovering a DP-spectrum that matches our theory for OLS. This validates the DP-estimator in a nontrivial ML application, opening the door to its use in more complex nonlinear ML settings where theory is unavailable.

PD-ML-Lite: Private Distributed Machine Learning from Lighweight Cryptography

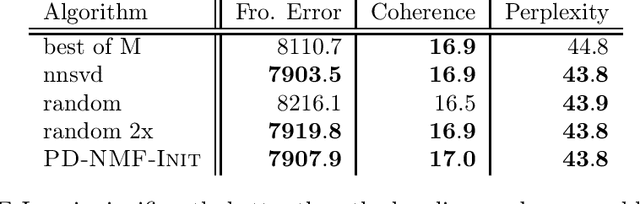
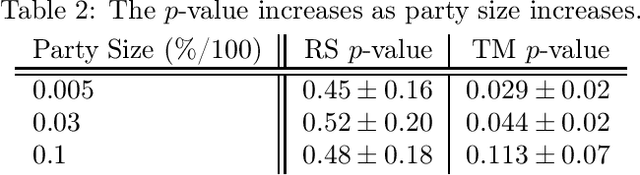
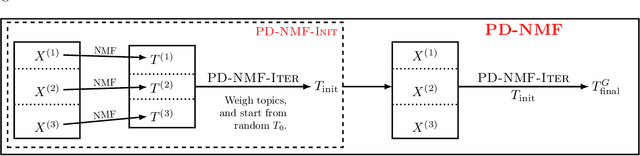
Privacy is a major issue in learning from distributed data. Recently the cryptographic literature has provided several tools for this task. However, these tools either reduce the quality/accuracy of the learning algorithm---e.g., by adding noise---or they incur a high performance penalty and/or involve trusting external authorities. We propose a methodology for {\sl private distributed machine learning from light-weight cryptography} (in short, PD-ML-Lite). We apply our methodology to two major ML algorithms, namely non-negative matrix factorization (NMF) and singular value decomposition (SVD). Our resulting protocols are communication optimal, achieve the same accuracy as their non-private counterparts, and satisfy a notion of privacy---which we define---that is both intuitive and measurable. Our approach is to use lightweight cryptographic protocols (secure sum and normalized secure sum) to build learning algorithms rather than wrap complex learning algorithms in a heavy-cost MPC framework. We showcase our algorithms' utility and privacy on several applications: for NMF we consider topic modeling and recommender systems, and for SVD, principal component regression, and low rank approximation.