PD-ML-Lite: Private Distributed Machine Learning from Lighweight Cryptography
Paper and Code
Jan 23, 2019
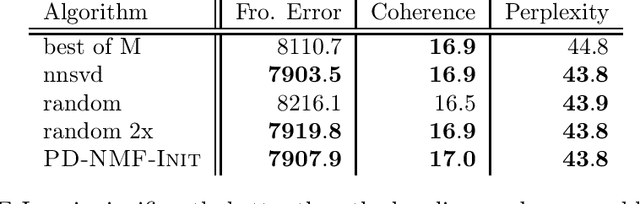
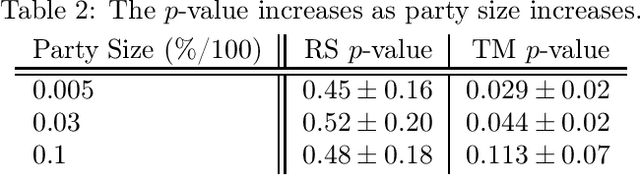
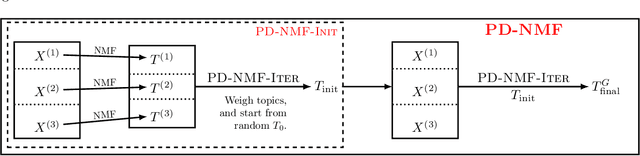
Privacy is a major issue in learning from distributed data. Recently the cryptographic literature has provided several tools for this task. However, these tools either reduce the quality/accuracy of the learning algorithm---e.g., by adding noise---or they incur a high performance penalty and/or involve trusting external authorities. We propose a methodology for {\sl private distributed machine learning from light-weight cryptography} (in short, PD-ML-Lite). We apply our methodology to two major ML algorithms, namely non-negative matrix factorization (NMF) and singular value decomposition (SVD). Our resulting protocols are communication optimal, achieve the same accuracy as their non-private counterparts, and satisfy a notion of privacy---which we define---that is both intuitive and measurable. Our approach is to use lightweight cryptographic protocols (secure sum and normalized secure sum) to build learning algorithms rather than wrap complex learning algorithms in a heavy-cost MPC framework. We showcase our algorithms' utility and privacy on several applications: for NMF we consider topic modeling and recommender systems, and for SVD, principal component regression, and low rank approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge