LingLanMiDian: Systematic Evaluation of LLMs on TCM Knowledge and Clinical Reasoning

Large language models (LLMs) are advancing rapidly in medical NLP, yet Traditional Chinese Medicine (TCM) with its distinctive ontology, terminology, and reasoning patterns requires domain-faithful evaluation. Existing TCM benchmarks are fragmented in coverage and scale and rely on non-unified or generation-heavy scoring that hinders fair comparison. We present the LingLanMiDian (LingLan) benchmark, a large-scale, expert-curated, multi-task suite that unifies evaluation across knowledge recall, multi-hop reasoning, information extraction, and real-world clinical decision-making. LingLan introduces a consistent metric design, a synonym-tolerant protocol for clinical labels, a per-dataset 400-item Hard subset, and a reframing of diagnosis and treatment recommendation into single-choice decision recognition. We conduct comprehensive, zero-shot evaluations on 14 leading open-source and proprietary LLMs, providing a unified perspective on their strengths and limitations in TCM commonsense knowledge understanding, reasoning, and clinical decision support; critically, the evaluation on Hard subset reveals a substantial gap between current models and human experts in TCM-specialized reasoning. By bridging fundamental knowledge and applied reasoning through standardized evaluation, LingLan establishes a unified, quantitative, and extensible foundation for advancing TCM LLMs and domain-specific medical AI research. All evaluation data and code are available at https://github.com/TCMAI-BJTU/LingLan and http://tcmnlp.com.

Privacy-Utility Tradeoff of OLS with Random Projections

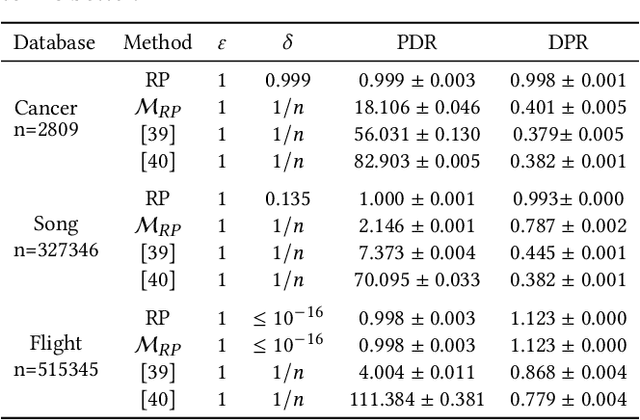
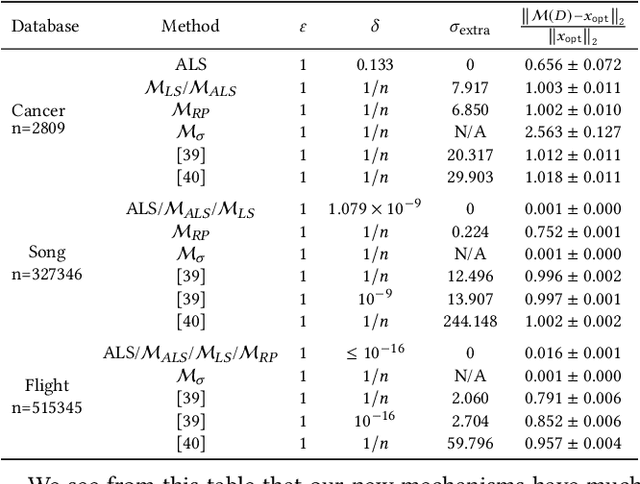
We study the differential privacy (DP) of a core ML problem, linear ordinary least squares (OLS), a.k.a. $\ell_2$-regression. Our key result is that the approximate LS algorithm (ALS) (Sarlos, 2006), a randomized solution to the OLS problem primarily used to improve performance on large datasets, also preserves privacy. ALS achieves a better privacy/utility tradeoff, without modifications or further noising, when compared to alternative private OLS algorithms which modify and/or noise OLS. We give the first {\em tight} DP-analysis for the ALS algorithm and the standard Gaussian mechanism (Dwork et al., 2014) applied to OLS. Our methodology directly improves the privacy analysis of (Blocki et al., 2012) and (Sheffet, 2019)) and introduces new tools which may be of independent interest: (1) the exact spectrum of $(\epsilon, \delta)$-DP parameters (``DP spectrum") for mechanisms whose output is a $d$-dimensional Gaussian, and (2) an improved DP spectrum for random projection (compared to (Blocki et al., 2012) and (Sheffet, 2019)). All methods for private OLS (including ours) assume, often implicitly, restrictions on the input database, such as bounds on leverage and residuals. We prove that such restrictions are necessary. Hence, computing the privacy of mechanisms such as ALS must estimate these database parameters, which can be infeasible in big datasets. For more complex ML models, DP bounds may not even be tractable. There is a need for blackbox DP-estimators (Lu et al., 2022) which empirically estimate a data-dependent privacy. We demonstrate the effectiveness of such a DP-estimator by empirically recovering a DP-spectrum that matches our theory for OLS. This validates the DP-estimator in a nontrivial ML application, opening the door to its use in more complex nonlinear ML settings where theory is unavailable.

A Comparison of First-order Algorithms for Machine Learning

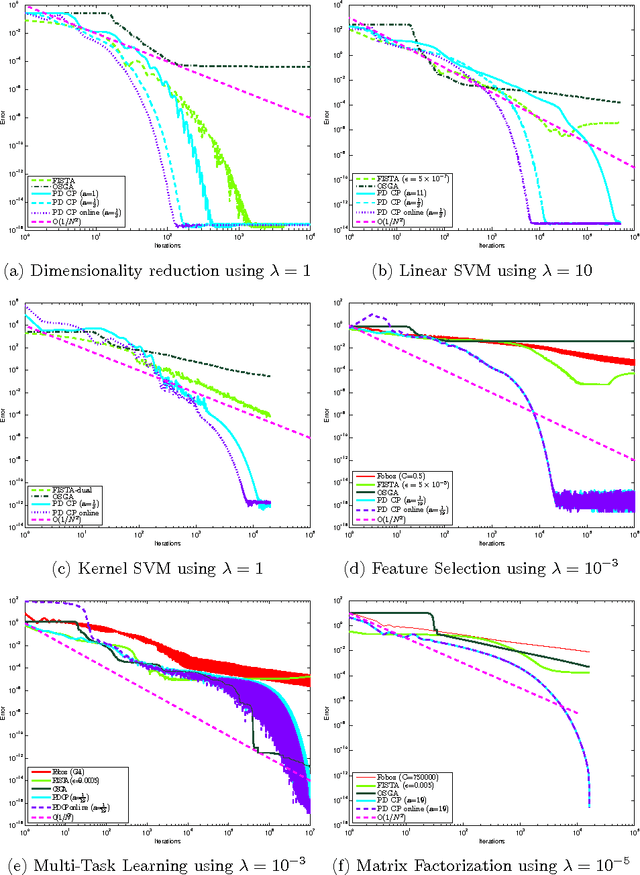
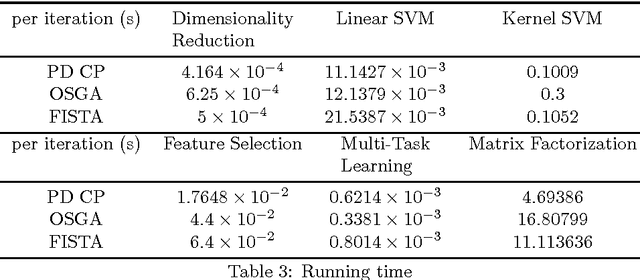
Using an optimization algorithm to solve a machine learning problem is one of mainstreams in the field of science. In this work, we demonstrate a comprehensive comparison of some state-of-the-art first-order optimization algorithms for convex optimization problems in machine learning. We concentrate on several smooth and non-smooth machine learning problems with a loss function plus a regularizer. The overall experimental results show the superiority of primal-dual algorithms in solving a machine learning problem from the perspectives of the ease to construct, running time and accuracy.