Exploring FPGA designs for MX and beyond

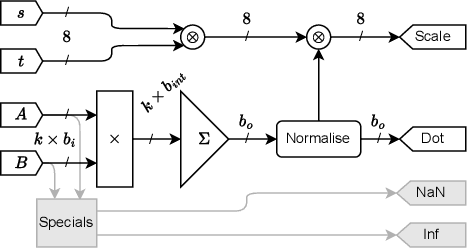
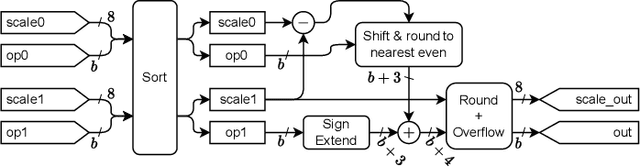
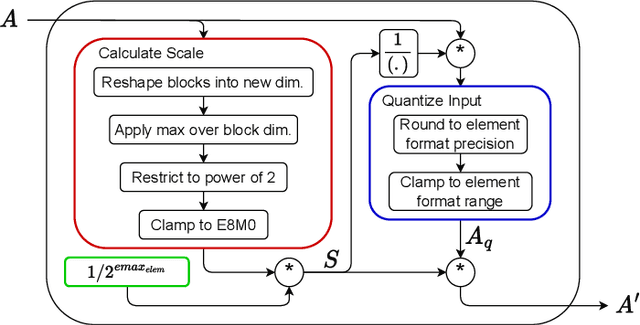
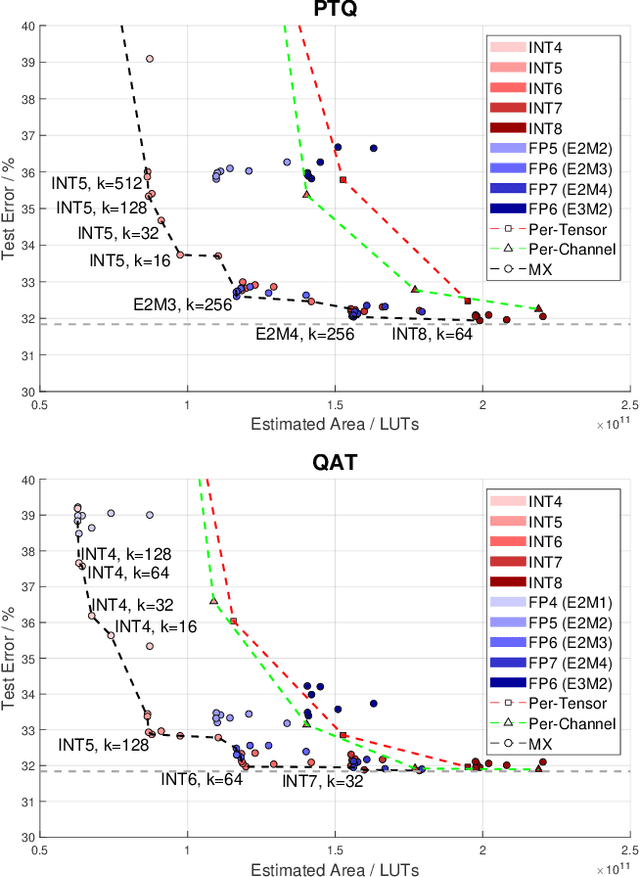
A number of companies recently worked together to release the new Open Compute Project MX standard for low-precision computation, aimed at efficient neural network implementation. In this paper, we describe and evaluate the first open-source FPGA implementation of the arithmetic defined in the standard. Our designs fully support all the standard's concrete formats for conversion into and out of MX formats and for the standard-defined arithmetic operations, as well as arbitrary fixed-point and floating-point formats. Certain elements of the standard are left as implementation-defined, and we present the first concrete FPGA-inspired choices for these elements, which we outline in the paper. Our library of optimized hardware components is available open source, and can be used to build larger systems. For this purpose, we also describe and release an open-source Pytorch library for quantization into the new standard, integrated with the Brevitas library so that the community can develop novel neural network designs quantized with MX formats in mind. We demonstrate the usability and efficacy of our libraries via the implementation of example neural networks such as ResNet-18 on the ImageNet ILSVRC12 dataset. Our testing shows that MX is very effective for formats such as INT5 or FP6 which are not natively supported on GPUs. This gives FPGAs an advantage as they have the flexibility to implement a custom datapath and take advantage of the smaller area footprints offered by these formats.

Efficient Post-training Quantization with FP8 Formats

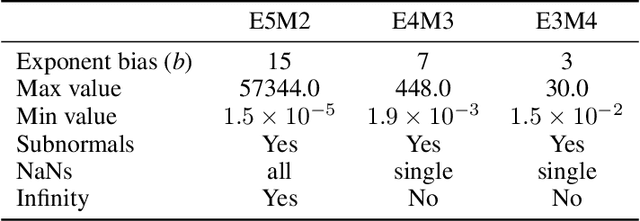
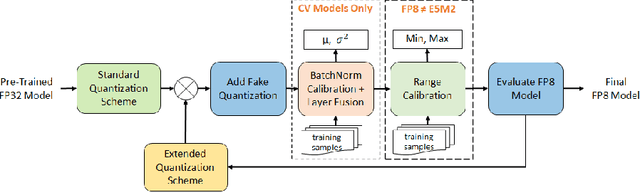
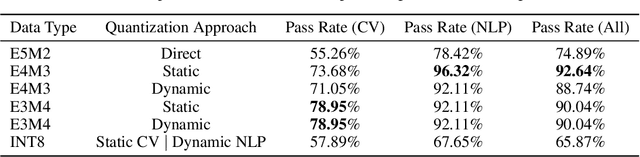
Recent advances in deep learning methods such as LLMs and Diffusion models have created a need for improved quantization methods that can meet the computational demands of these modern architectures while maintaining accuracy. Towards this goal, we study the advantages of FP8 data formats for post-training quantization across 75 unique network architectures covering a wide range of tasks, including machine translation, language modeling, text generation, image classification, generation, and segmentation. We examine three different FP8 representations (E5M2, E4M3, and E3M4) to study the effects of varying degrees of trade-off between dynamic range and precision on model accuracy. Based on our extensive study, we developed a quantization workflow that generalizes across different network architectures. Our empirical results show that FP8 formats outperform INT8 in multiple aspects, including workload coverage (92.64% vs. 65.87%), model accuracy and suitability for a broader range of operations. Furthermore, our findings suggest that E4M3 is better suited for NLP models, whereas E3M4 performs marginally better than E4M3 on computer vision tasks. The code is publicly available on Intel Neural Compressor: https://github.com/intel/neural-compressor.

FP8 Formats for Deep Learning

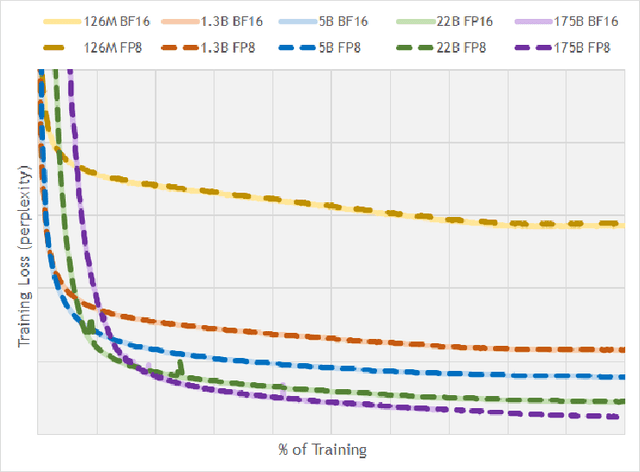
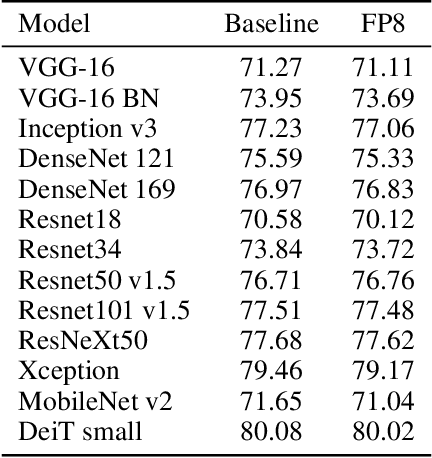
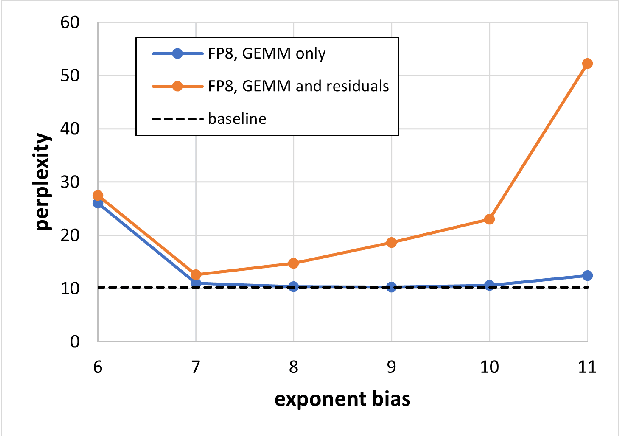
FP8 is a natural progression for accelerating deep learning training inference beyond the 16-bit formats common in modern processors. In this paper we propose an 8-bit floating point (FP8) binary interchange format consisting of two encodings - E4M3 (4-bit exponent and 3-bit mantissa) and E5M2 (5-bit exponent and 2-bit mantissa). While E5M2 follows IEEE 754 conventions for representatio of special values, E4M3's dynamic range is extended by not representing infinities and having only one mantissa bit-pattern for NaNs. We demonstrate the efficacy of the FP8 format on a variety of image and language tasks, effectively matching the result quality achieved by 16-bit training sessions. Our study covers the main modern neural network architectures - CNNs, RNNs, and Transformer-based models, leaving all the hyperparameters unchanged from the 16-bit baseline training sessions. Our training experiments include large, up to 175B parameter, language models. We also examine FP8 post-training-quantization of language models trained using 16-bit formats that resisted fixed point int8 quantization.

High Performance Scalable FPGA Accelerator for Deep Neural Networks

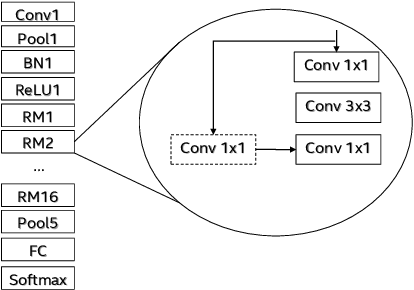
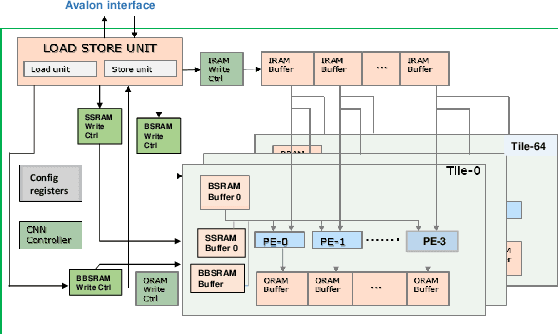
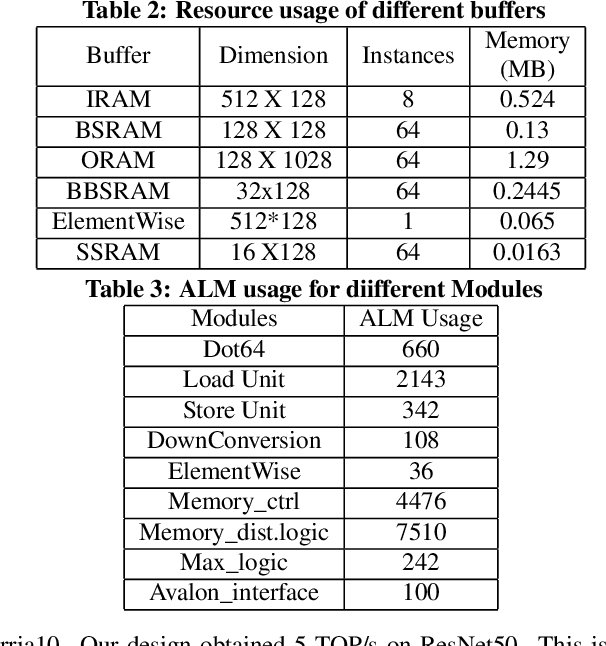
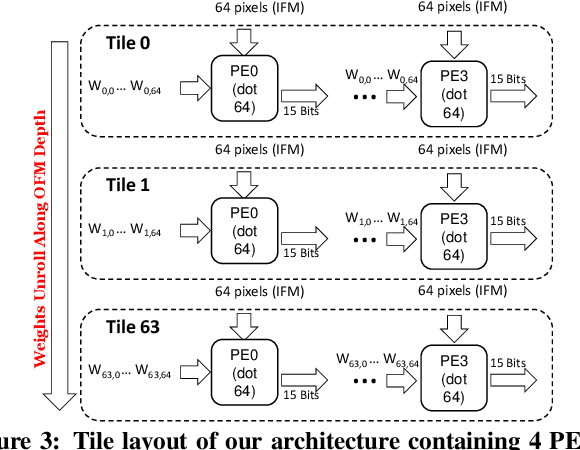
Low-precision is the first order knob for achieving higher Artificial Intelligence Operations (AI-TOPS). However the algorithmic space for sub-8-bit precision compute is diverse, with disruptive changes happening frequently, making FPGAs a natural choice for Deep Neural Network inference, In this work we present an FPGA-based accelerator for CNN inference acceleration. We use {\it INT-8-2} compute (with {\it 8 bit} activation and {2 bit} weights) which is recently showing promise in the literature, and which no known ASIC, CPU or GPU natively supports today. Using a novel Adaptive Logic Module (ALM) based design, as a departure from traditional DSP based designs, we are able to achieve high performance measurement of 5 AI-TOPS for {\it Arria10} and project a performance of 76 AI-TOPS at 0.7 TOPS/W for {\it Stratix10}. This exceeds known CPU, GPU performance and comes close to best known ASIC (TPU) numbers, while retaining the versatility of the FPGA platform for other applications.

A Study of BFLOAT16 for Deep Learning Training

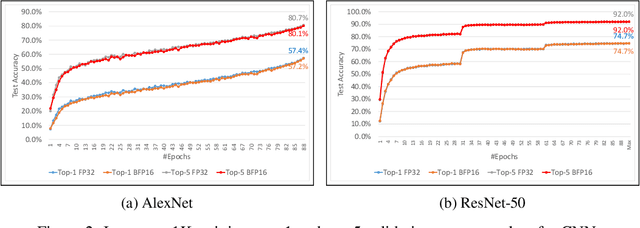
This paper presents the first comprehensive empirical study demonstrating the efficacy of the Brain Floating Point (BFLOAT16) half-precision format for Deep Learning training across image classification, speech recognition, language modeling, generative networks and industrial recommendation systems. BFLOAT16 is attractive for Deep Learning training for two reasons: the range of values it can represent is the same as that of IEEE 754 floating-point format (FP32) and conversion to/from FP32 is simple. Maintaining the same range as FP32 is important to ensure that no hyper-parameter tuning is required for convergence; e.g., IEEE 754 compliant half-precision floating point (FP16) requires hyper-parameter tuning. In this paper, we discuss the flow of tensors and various key operations in mixed precision training, and delve into details of operations, such as the rounding modes for converting FP32 tensors to BFLOAT16. We have implemented a method to emulate BFLOAT16 operations in Tensorflow, Caffe2, IntelCaffe, and Neon for our experiments. Our results show that deep learning training using BFLOAT16 tensors achieves the same state-of-the-art (SOTA) results across domains as FP32 tensors in the same number of iterations and with no changes to hyper-parameters.

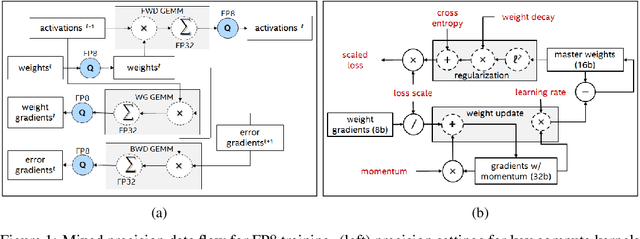
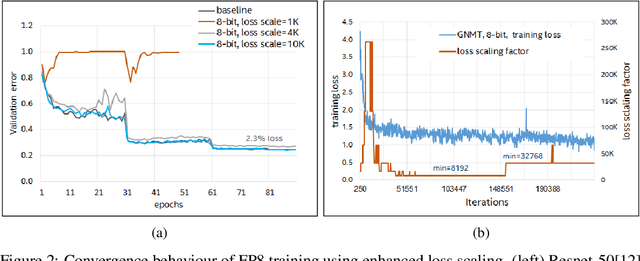
Mixed Precision Training With 8-bit Floating Point

Reduced precision computation for deep neural networks is one of the key areas addressing the widening compute gap driven by an exponential growth in model size. In recent years, deep learning training has largely migrated to 16-bit precision, with significant gains in performance and energy efficiency. However, attempts to train DNNs at 8-bit precision have met with significant challenges because of the higher precision and dynamic range requirements of back-propagation. In this paper, we propose a method to train deep neural networks using 8-bit floating point representation for weights, activations, errors, and gradients. In addition to reducing compute precision, we also reduced the precision requirements for the master copy of weights from 32-bit to 16-bit. We demonstrate state-of-the-art accuracy across multiple data sets (imagenet-1K, WMT16) and a broader set of workloads (Resnet-18/34/50, GNMT, Transformer) than previously reported. We propose an enhanced loss scaling method to augment the reduced subnormal range of 8-bit floating point for improved error propagation. We also examine the impact of quantization noise on generalization and propose a stochastic rounding technique to address gradient noise. As a result of applying all these techniques, we report slightly higher validation accuracy compared to full precision baseline.

Mixed Precision Training of Convolutional Neural Networks using Integer Operations

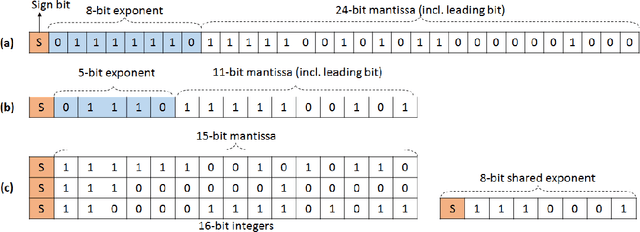
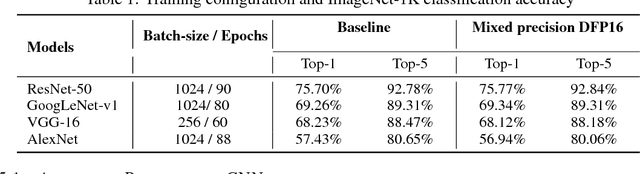
The state-of-the-art (SOTA) for mixed precision training is dominated by variants of low precision floating point operations, and in particular, FP16 accumulating into FP32 Micikevicius et al. (2017). On the other hand, while a lot of research has also happened in the domain of low and mixed-precision Integer training, these works either present results for non-SOTA networks (for instance only AlexNet for ImageNet-1K), or relatively small datasets (like CIFAR-10). In this work, we train state-of-the-art visual understanding neural networks on the ImageNet-1K dataset, with Integer operations on General Purpose (GP) hardware. In particular, we focus on Integer Fused-Multiply-and-Accumulate (FMA) operations which take two pairs of INT16 operands and accumulate results into an INT32 output.We propose a shared exponent representation of tensors and develop a Dynamic Fixed Point (DFP) scheme suitable for common neural network operations. The nuances of developing an efficient integer convolution kernel is examined, including methods to handle overflow of the INT32 accumulator. We implement CNN training for ResNet-50, GoogLeNet-v1, VGG-16 and AlexNet; and these networks achieve or exceed SOTA accuracy within the same number of iterations as their FP32 counterparts without any change in hyper-parameters and with a 1.8X improvement in end-to-end training throughput. To the best of our knowledge these results represent the first INT16 training results on GP hardware for ImageNet-1K dataset using SOTA CNNs and achieve highest reported accuracy using half-precision

On Scale-out Deep Learning Training for Cloud and HPC

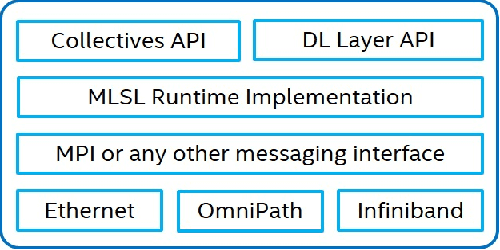
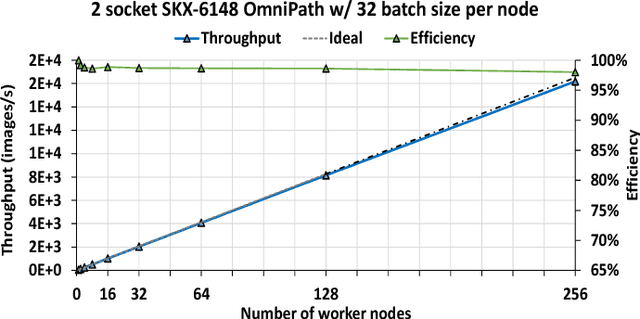
The exponential growth in use of large deep neural networks has accelerated the need for training these deep neural networks in hours or even minutes. This can only be achieved through scalable and efficient distributed training, since a single node/card cannot satisfy the compute, memory, and I/O requirements of today's state-of-the-art deep neural networks. However, scaling synchronous Stochastic Gradient Descent (SGD) is still a challenging problem and requires continued research/development. This entails innovations spanning algorithms, frameworks, communication libraries, and system design. In this paper, we describe the philosophy, design, and implementation of Intel Machine Learning Scalability Library (MLSL) and present proof-points demonstrating scaling DL training on 100s to 1000s of nodes across Cloud and HPC systems.

Ternary Residual Networks

Sub-8-bit representation of DNNs incur some discernible loss of accuracy despite rigorous (re)training at low-precision. Such loss of accuracy essentially makes them equivalent to a much shallower counterpart, diminishing the power of being deep networks. To address this problem of accuracy drop we introduce the notion of \textit{residual networks} where we add more low-precision edges to sensitive branches of the sub-8-bit network to compensate for the lost accuracy. Further, we present a perturbation theory to identify such sensitive edges. Aided by such an elegant trade-off between accuracy and compute, the 8-2 model (8-bit activations, ternary weights), enhanced by ternary residual edges, turns out to be sophisticated enough to achieve very high accuracy ($\sim 1\%$ drop from our FP-32 baseline), despite $\sim 1.6\times$ reduction in model size, $\sim 26\times$ reduction in number of multiplications, and potentially $\sim 2\times$ power-performance gain comparing to 8-8 representation, on the state-of-the-art deep network ResNet-101 pre-trained on ImageNet dataset. Moreover, depending on the varying accuracy requirements in a dynamic environment, the deployed low-precision model can be upgraded/downgraded on-the-fly by partially enabling/disabling residual connections. For example, disabling the least important residual connections in the above enhanced network, the accuracy drop is $\sim 2\%$ (from FP32), despite $\sim 1.9\times$ reduction in model size, $\sim 32\times$ reduction in number of multiplications, and potentially $\sim 2.3\times$ power-performance gain comparing to 8-8 representation. Finally, all the ternary connections are sparse in nature, and the ternary residual conversion can be done in a resource-constraint setting with no low-precision (re)training.

Ternary Neural Networks with Fine-Grained Quantization

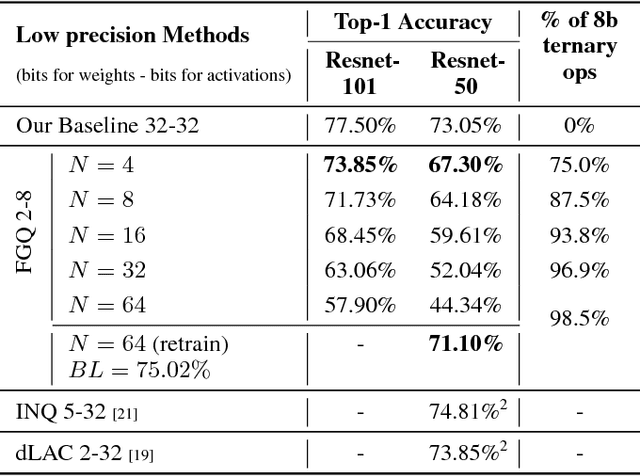
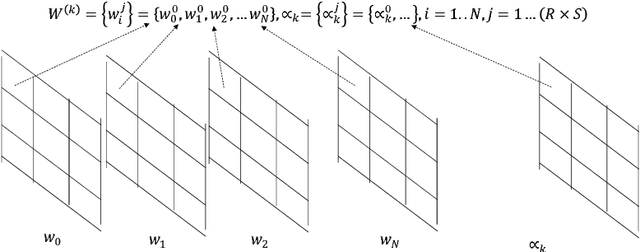
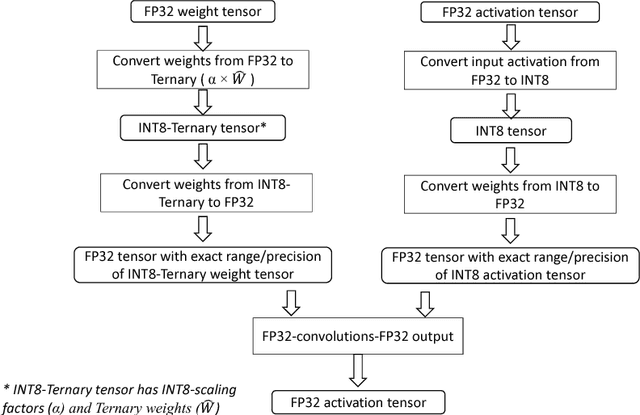
We propose a novel fine-grained quantization (FGQ) method to ternarize pre-trained full precision models, while also constraining activations to 8 and 4-bits. Using this method, we demonstrate a minimal loss in classification accuracy on state-of-the-art topologies without additional training. We provide an improved theoretical formulation that forms the basis for a higher quality solution using FGQ. Our method involves ternarizing the original weight tensor in groups of $N$ weights. Using $N=4$, we achieve Top-1 accuracy within $3.7\%$ and $4.2\%$ of the baseline full precision result for Resnet-101 and Resnet-50 respectively, while eliminating $75\%$ of all multiplications. These results enable a full 8/4-bit inference pipeline, with best-reported accuracy using ternary weights on ImageNet dataset, with a potential of $9\times$ improvement in performance. Also, for smaller networks like AlexNet, FGQ achieves state-of-the-art results. We further study the impact of group size on both performance and accuracy. With a group size of $N=64$, we eliminate $\approx99\%$ of the multiplications; however, this introduces a noticeable drop in accuracy, which necessitates fine tuning the parameters at lower precision. We address this by fine-tuning Resnet-50 with 8-bit activations and ternary weights at $N=64$, improving the Top-1 accuracy to within $4\%$ of the full precision result with $<30\%$ additional training overhead. Our final quantized model can run on a full 8-bit compute pipeline using 2-bit weights and has the potential of up to $15\times$ improvement in performance compared to baseline full-precision models.