Dusan Stosic
Quantization-Aware Distillation for NVFP4 Inference Accuracy Recovery
Jan 27, 2026Abstract:This technical report presents quantization-aware distillation (QAD) and our best practices for recovering accuracy of NVFP4-quantized large language models (LLMs) and vision-language models (VLMs). QAD distills a full-precision teacher model into a quantized student model using a KL divergence loss. While applying distillation to quantized models is not a new idea, we observe key advantages of QAD for today's LLMs: 1. It shows remarkable effectiveness and stability for models trained through multi-stage post-training pipelines, including supervised fine-tuning (SFT), reinforcement learning (RL), and model merging, where traditional quantization-aware training (QAT) suffers from engineering complexity and training instability; 2. It is robust to data quality and coverage, enabling accuracy recovery without full training data. We evaluate QAD across multiple post-trained models including AceReason Nemotron, Nemotron 3 Nano, Nemotron Nano V2, Nemotron Nano V2 VL (VLM), and Llama Nemotron Super v1, showing consistent recovery to near-BF16 accuracy.
NVIDIA Nemotron 3: Efficient and Open Intelligence
Dec 24, 2025Abstract:We introduce the Nemotron 3 family of models - Nano, Super, and Ultra. These models deliver strong agentic, reasoning, and conversational capabilities. The Nemotron 3 family uses a Mixture-of-Experts hybrid Mamba-Transformer architecture to provide best-in-class throughput and context lengths of up to 1M tokens. Super and Ultra models are trained with NVFP4 and incorporate LatentMoE, a novel approach that improves model quality. The two larger models also include MTP layers for faster text generation. All Nemotron 3 models are post-trained using multi-environment reinforcement learning enabling reasoning, multi-step tool use, and support granular reasoning budget control. Nano, the smallest model, outperforms comparable models in accuracy while remaining extremely cost-efficient for inference. Super is optimized for collaborative agents and high-volume workloads such as IT ticket automation. Ultra, the largest model, provides state-of-the-art accuracy and reasoning performance. Nano is released together with its technical report and this white paper, while Super and Ultra will follow in the coming months. We will openly release the model weights, pre- and post-training software, recipes, and all data for which we hold redistribution rights.
Nemotron 3 Nano: Open, Efficient Mixture-of-Experts Hybrid Mamba-Transformer Model for Agentic Reasoning
Dec 23, 2025Abstract:We present Nemotron 3 Nano 30B-A3B, a Mixture-of-Experts hybrid Mamba-Transformer language model. Nemotron 3 Nano was pretrained on 25 trillion text tokens, including more than 3 trillion new unique tokens over Nemotron 2, followed by supervised fine tuning and large-scale RL on diverse environments. Nemotron 3 Nano achieves better accuracy than our previous generation Nemotron 2 Nano while activating less than half of the parameters per forward pass. It achieves up to 3.3x higher inference throughput than similarly-sized open models like GPT-OSS-20B and Qwen3-30B-A3B-Thinking-2507, while also being more accurate on popular benchmarks. Nemotron 3 Nano demonstrates enhanced agentic, reasoning, and chat abilities and supports context lengths up to 1M tokens. We release both our pretrained Nemotron 3 Nano 30B-A3B Base and post-trained Nemotron 3 Nano 30B-A3B checkpoints on Hugging Face.
Nemotron-H: A Family of Accurate and Efficient Hybrid Mamba-Transformer Models
Apr 10, 2025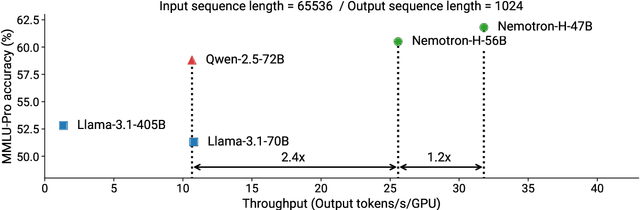

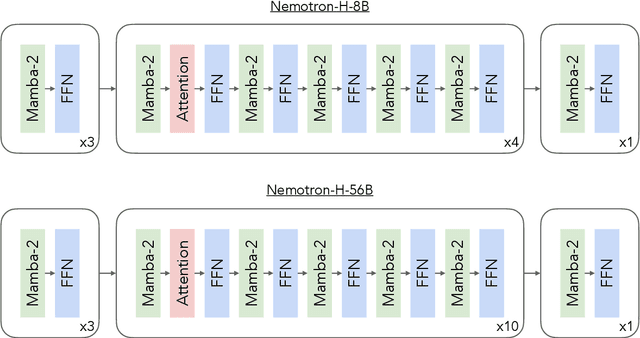
Abstract:As inference-time scaling becomes critical for enhanced reasoning capabilities, it is increasingly becoming important to build models that are efficient to infer. We introduce Nemotron-H, a family of 8B and 56B/47B hybrid Mamba-Transformer models designed to reduce inference cost for a given accuracy level. To achieve this goal, we replace the majority of self-attention layers in the common Transformer model architecture with Mamba layers that perform constant computation and require constant memory per generated token. We show that Nemotron-H models offer either better or on-par accuracy compared to other similarly-sized state-of-the-art open-sourced Transformer models (e.g., Qwen-2.5-7B/72B and Llama-3.1-8B/70B), while being up to 3$\times$ faster at inference. To further increase inference speed and reduce the memory required at inference time, we created Nemotron-H-47B-Base from the 56B model using a new compression via pruning and distillation technique called MiniPuzzle. Nemotron-H-47B-Base achieves similar accuracy to the 56B model, but is 20% faster to infer. In addition, we introduce an FP8-based training recipe and show that it can achieve on par results with BF16-based training. This recipe is used to train the 56B model. All Nemotron-H models will be released, with support in Hugging Face, NeMo, and Megatron-LM.
FP8 Formats for Deep Learning
Sep 12, 2022
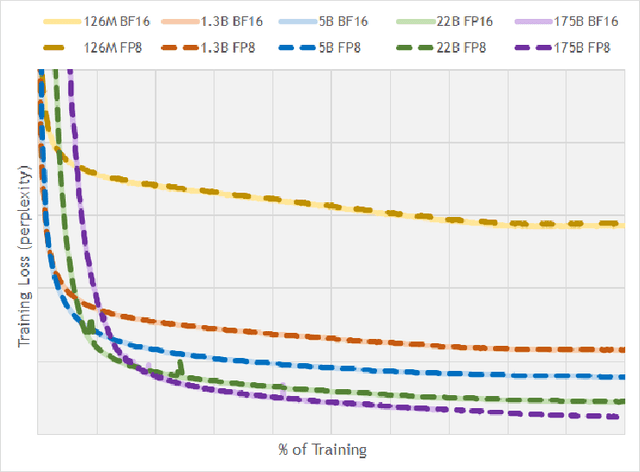
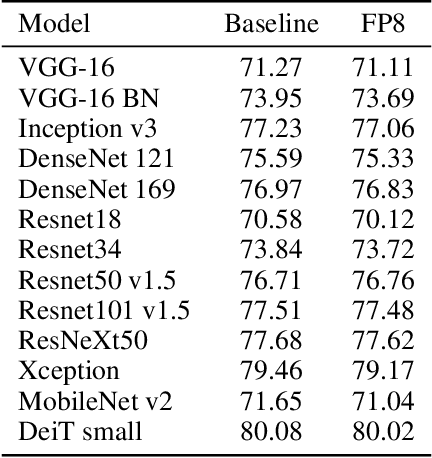
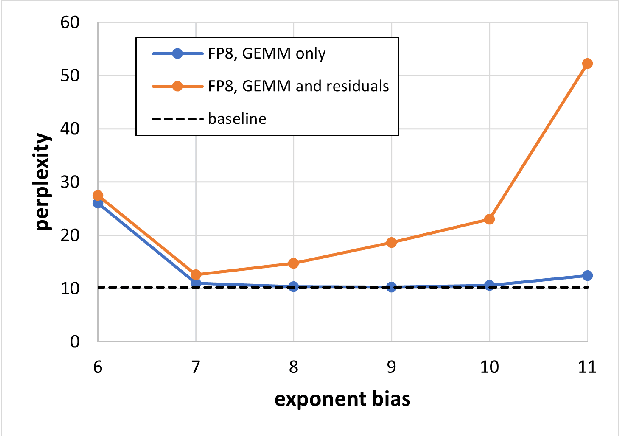
Abstract:FP8 is a natural progression for accelerating deep learning training inference beyond the 16-bit formats common in modern processors. In this paper we propose an 8-bit floating point (FP8) binary interchange format consisting of two encodings - E4M3 (4-bit exponent and 3-bit mantissa) and E5M2 (5-bit exponent and 2-bit mantissa). While E5M2 follows IEEE 754 conventions for representatio of special values, E4M3's dynamic range is extended by not representing infinities and having only one mantissa bit-pattern for NaNs. We demonstrate the efficacy of the FP8 format on a variety of image and language tasks, effectively matching the result quality achieved by 16-bit training sessions. Our study covers the main modern neural network architectures - CNNs, RNNs, and Transformer-based models, leaving all the hyperparameters unchanged from the 16-bit baseline training sessions. Our training experiments include large, up to 175B parameter, language models. We also examine FP8 post-training-quantization of language models trained using 16-bit formats that resisted fixed point int8 quantization.
Distance Metric Learning through Minimization of the Free Energy
Jun 10, 2021

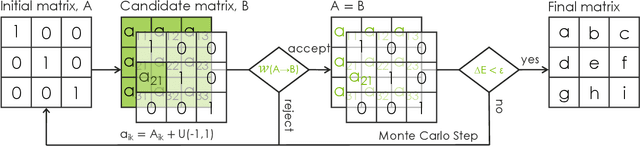

Abstract:Distance metric learning has attracted a lot of interest for solving machine learning and pattern recognition problems over the last decades. In this work we present a simple approach based on concepts from statistical physics to learn optimal distance metric for a given problem. We formulate the task as a typical statistical physics problem: distances between patterns represent constituents of a physical system and the objective function corresponds to energy. Then we express the problem as a minimization of the free energy of a complex system, which is equivalent to distance metric learning. Much like for many problems in physics, we propose an approach based on Metropolis Monte Carlo to find the best distance metric. This provides a natural way to learn the distance metric, where the learning process can be intuitively seen as stretching and rotating the metric space until some heuristic is satisfied. Our proposed method can handle a wide variety of constraints including those with spurious local minima. The approach works surprisingly well with stochastic nearest neighbors from neighborhood component analysis (NCA). Experimental results on artificial and real-world data sets reveal a clear superiority over a number of state-of-the-art distance metric learning methods for nearest neighbors classification.
Search Spaces for Neural Model Training
May 27, 2021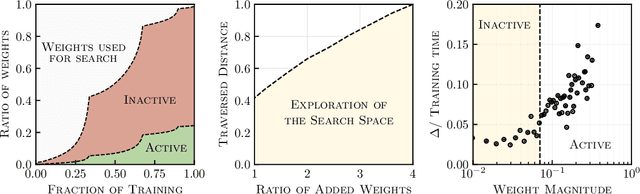



Abstract:While larger neural models are pushing the boundaries of what deep learning can do, often more weights are needed to train models rather than to run inference for tasks. This paper seeks to understand this behavior using search spaces -- adding weights creates extra degrees of freedom that form new paths for optimization (or wider search spaces) rendering neural model training more effective. We then show how we can augment search spaces to train sparse models attaining competitive scores across dozens of deep learning workloads. They are also are tolerant of structures targeting current hardware, opening avenues for training and inference acceleration. Our work encourages research to explore beyond massive neural models being used today.
Accelerating Sparse Deep Neural Networks
Apr 16, 2021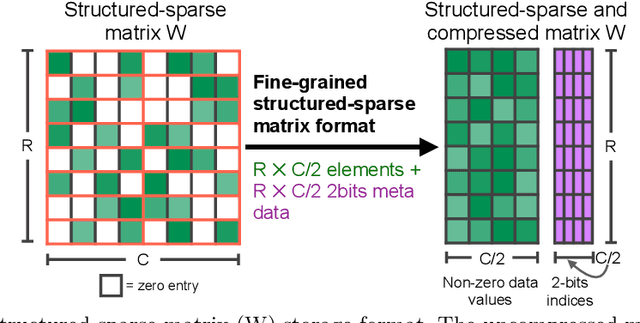
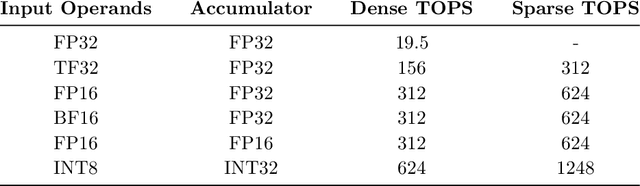
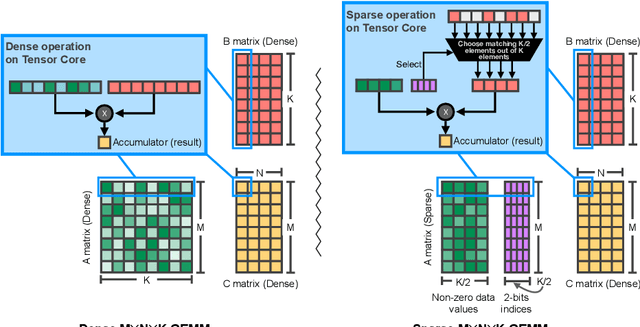
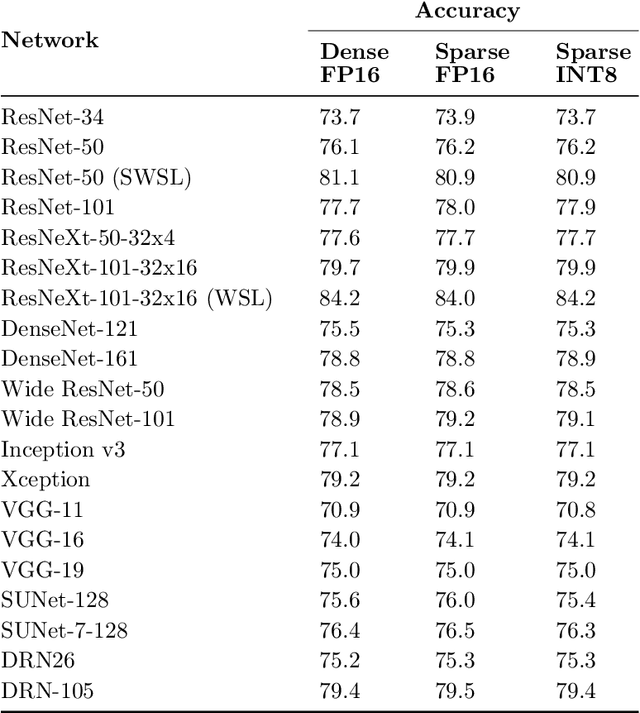
Abstract:As neural network model sizes have dramatically increased, so has the interest in various techniques to reduce their parameter counts and accelerate their execution. An active area of research in this field is sparsity - encouraging zero values in parameters that can then be discarded from storage or computations. While most research focuses on high levels of sparsity, there are challenges in universally maintaining model accuracy as well as achieving significant speedups over modern matrix-math hardware. To make sparsity adoption practical, the NVIDIA Ampere GPU architecture introduces sparsity support in its matrix-math units, Tensor Cores. We present the design and behavior of Sparse Tensor Cores, which exploit a 2:4 (50%) sparsity pattern that leads to twice the math throughput of dense matrix units. We also describe a simple workflow for training networks that both satisfy 2:4 sparsity pattern requirements and maintain accuracy, verifying it on a wide range of common tasks and model architectures. This workflow makes it easy to prepare accurate models for efficient deployment on Sparse Tensor Cores.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge