About rectified sigmoid function for enhancing the accuracy of Physics-Informed Neural Networks

The article is devoted to the study of neural networks with one hidden layer and a modified activation function for solving physical problems. A rectified sigmoid activation function has been proposed to solve physical problems described by the ODE with neural networks. Algorithms for physics-informed data-driven initialization of a neural network and a neuron-by-neuron gradient-free fitting method have been presented for the neural network with this activation function. Numerical experiments demonstrate the superiority of neural networks with a rectified sigmoid function over neural networks with a sigmoid function in the accuracy of solving physical problems (harmonic oscillator, relativistic slingshot, and Lorentz system).

Are Two Hidden Layers Still Enough for the Physics-Informed Neural Networks?

The article discusses the development of various methods and techniques for initializing and training neural networks with a single hidden layer, as well as training a separable physics-informed neural network consisting of neural networks with a single hidden layer to solve physical problems described by ordinary differential equations (ODEs) and partial differential equations (PDEs). A method for strictly deterministic initialization of a neural network with one hidden layer for solving physical problems described by an ODE is proposed. Modifications to existing methods for weighting the loss function are given, as well as new methods developed for training strictly deterministic-initialized neural networks to solve ODEs (detaching, additional weighting based on the second derivative, predicted solution-based weighting, relative residuals). An algorithm for physics-informed data-driven initialization of a neural network with one hidden layer is proposed. A neural network with pronounced generalizing properties is presented, whose generalizing abilities of which can be precisely controlled by adjusting network parameters. A metric for measuring the generalization of such neural network has been introduced. A gradient-free neuron-by-neuron fitting method has been developed for adjusting the parameters of a single-hidden-layer neural network, which does not require the use of an optimizer or solver for its implementation. The proposed methods have been extended to 2D problems using the separable physics-informed neural networks approach. Numerous experiments have been carried out to develop the above methods and approaches. Experiments on physical problems, such as solving various ODEs and PDEs, have demonstrated that these methods for initializing and training neural networks with one or two hidden layers (SPINN) achieve competitive accuracy and, in some cases, state-of-the-art results.

Separable Physics-Informed Neural Networks for the solution of elasticity problems

A method for solving elasticity problems based on separable physics-informed neural networks (SPINN) in conjunction with the deep energy method (DEM) is presented. Numerical experiments have been carried out for a number of problems showing that this method has a significantly higher convergence rate and accuracy than the vanilla physics-informed neural networks (PINN) and even SPINN based on a system of partial differential equations (PDEs). In addition, using the SPINN in the framework of DEM approach it is possible to solve problems of the linear theory of elasticity on complex geometries, which is unachievable with the help of PINNs in frames of partial differential equations. Considered problems are very close to the industrial problems in terms of geometry, loading, and material parameters.

About optimal loss function for training physics-informed neural networks under respecting causality

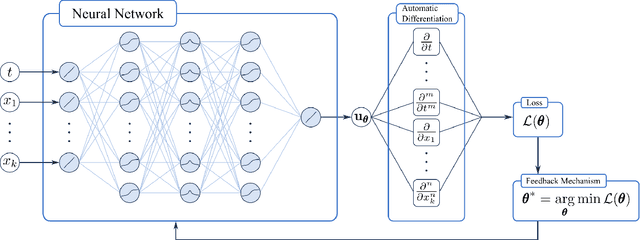
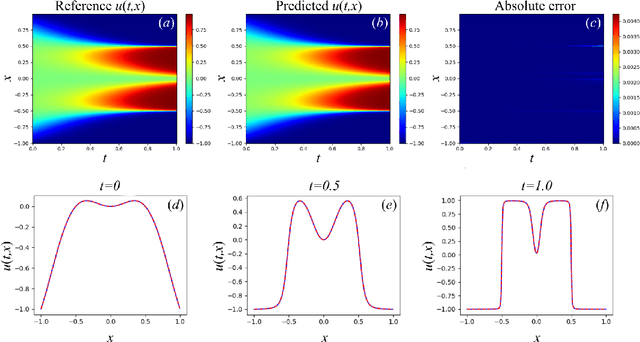
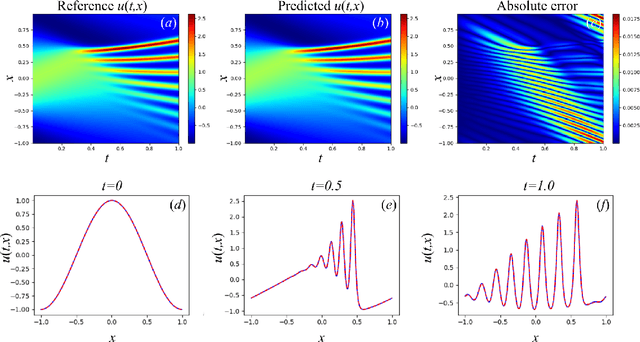
A method is presented that allows to reduce a problem described by differential equations with initial and boundary conditions to the problem described only by differential equations. The advantage of using the modified problem for physics-informed neural networks (PINNs) methodology is that it becomes possible to represent the loss function in the form of a single term associated with differential equations, thus eliminating the need to tune the scaling coefficients for the terms related to boundary and initial conditions. The weighted loss functions respecting causality were modified and new weighted loss functions based on generalized functions are derived. Numerical experiments have been carried out for a number of problems, demonstrating the accuracy of the proposed methods.

On Scale-out Deep Learning Training for Cloud and HPC

The exponential growth in use of large deep neural networks has accelerated the need for training these deep neural networks in hours or even minutes. This can only be achieved through scalable and efficient distributed training, since a single node/card cannot satisfy the compute, memory, and I/O requirements of today's state-of-the-art deep neural networks. However, scaling synchronous Stochastic Gradient Descent (SGD) is still a challenging problem and requires continued research/development. This entails innovations spanning algorithms, frameworks, communication libraries, and system design. In this paper, we describe the philosophy, design, and implementation of Intel Machine Learning Scalability Library (MLSL) and present proof-points demonstrating scaling DL training on 100s to 1000s of nodes across Cloud and HPC systems.