PolyLUT: Ultra-low Latency Polynomial Inference with Hardware-Aware Structured Pruning

Standard deep neural network inference involves the computation of interleaved linear maps and nonlinear activation functions. Prior work for ultra-low latency implementations has hardcoded these operations inside FPGA lookup tables (LUTs). However, FPGA LUTs can implement a much greater variety of functions. In this paper, we propose a novel approach to training DNNs for FPGA deployment using multivariate polynomials as the basic building block. Our method takes advantage of the flexibility offered by the soft logic, hiding the polynomial evaluation inside the LUTs with minimal overhead. By using polynomial building blocks, we achieve the same accuracy using considerably fewer layers of soft logic than by using linear functions, leading to significant latency and area improvements. LUT-based implementations also face a significant challenge: the LUT size grows exponentially with the number of inputs. Prior work relies on a priori fixed sparsity, with results heavily dependent on seed selection. To address this, we propose a structured pruning strategy using a bespoke hardware-aware group regularizer that encourages a particular sparsity pattern that leads to a small number of inputs per neuron. We demonstrate the effectiveness of PolyLUT on three tasks: network intrusion detection, jet identification at the CERN Large Hadron Collider, and MNIST.

ReducedLUT: Table Decomposition with "Don't Care" Conditions

Lookup tables (LUTs) are frequently used to efficiently store arrays of precomputed values for complex mathematical computations. When used in the context of neural networks, these functions exhibit a lack of recognizable patterns which presents an unusual challenge for conventional logic synthesis techniques. Several approaches are known to break down a single large lookup table into multiple smaller ones that can be recombined. Traditional methods, such as plain tabulation, piecewise linear approximation, and multipartite table methods, often yield inefficient hardware solutions when applied to LUT-based NNs. This paper introduces ReducedLUT, a novel method to reduce the footprint of the LUTs by injecting don't cares into the compression process. This additional freedom introduces more self-similarities which can be exploited using known decomposition techniques. We then demonstrate a particular application to machine learning; by replacing unobserved patterns within the training data of neural network models with don't cares, we enable greater compression with minimal model accuracy degradation. In practice, we achieve up to $1.63\times$ reduction in Physical LUT utilization, with a test accuracy drop of no more than $0.01$ accuracy points.

BitMoD: Bit-serial Mixture-of-Datatype LLM Acceleration

Large language models (LLMs) have demonstrated remarkable performance across various machine learning tasks. Yet the substantial memory footprint of LLMs significantly hinders their deployment. In this paper, we improve the accessibility of LLMs through BitMoD, an algorithm-hardware co-design solution that enables efficient LLM acceleration at low weight precision. On the algorithm side, BitMoD introduces fine-grained data type adaptation that uses a different numerical data type to quantize a group of (e.g., 128) weights. Through the careful design of these new data types, BitMoD is able to quantize LLM weights to very low precision (e.g., 4 bits and 3 bits) while maintaining high accuracy. On the hardware side, BitMoD employs a bit-serial processing element to easily support multiple numerical precisions and data types; our hardware design includes two key innovations: First, it employs a unified representation to process different weight data types, thus reducing the hardware cost. Second, it adopts a bit-serial dequantization unit to rescale the per-group partial sum with minimal hardware overhead. Our evaluation on six representative LLMs demonstrates that BitMoD significantly outperforms state-of-the-art LLM quantization and acceleration methods. For discriminative tasks, BitMoD can quantize LLM weights to 4-bit with $<\!0.5\%$ accuracy loss on average. For generative tasks, BitMoD is able to quantize LLM weights to 3-bit while achieving better perplexity than prior LLM quantization scheme. Combining the superior model performance with an efficient accelerator design, BitMoD achieves an average of $1.69\times$ and $1.48\times$ speedups compared to prior LLM accelerators ANT and OliVe, respectively.

QERA: an Analytical Framework for Quantization Error Reconstruction

he growing number of parameters and computational demands of large language models (LLMs) present significant challenges for their efficient deployment. Recently, there is an increasing interest in quantizing weights to extremely low precision while offsetting the resulting error with low-rank, high-precision error reconstruction terms. The combination of quantization and low-rank approximation is now popular in both adapter-based, parameter-efficient fine-tuning methods such as LoftQ and low-precision inference techniques including ZeroQuant-V2. Usually, the low-rank terms are calculated via the singular value decomposition (SVD) of the weight quantization error, minimizing the Frobenius and spectral norms of the weight approximation error. Recent methods like LQ-LoRA and LQER introduced hand-crafted heuristics to minimize errors in layer outputs (activations) rather than weights, resulting improved quantization results. However, these heuristic methods lack an analytical solution to guide the design of quantization error reconstruction terms. In this paper, we revisit this problem and formulate an analytical framework, named Quantization Error Reconstruction Analysis (QERA), and offer a closed-form solution to the problem. We show QERA benefits both existing low-precision fine-tuning and inference methods -- QERA achieves a fine-tuned accuracy gain of $\Delta_{\text{acc}}$ = 6.05% of 2-bit RoBERTa-base on GLUE compared to LoftQ; and obtains $\Delta_{\text{acc}}$ = 2.97% higher post-training quantization accuracy of 4-bit Llama-3.1-70B on average than ZeroQuant-V2 and $\Delta_{\text{ppl}}$ = - 0.28 lower perplexity on WikiText2 than LQER.

Exploring FPGA designs for MX and beyond

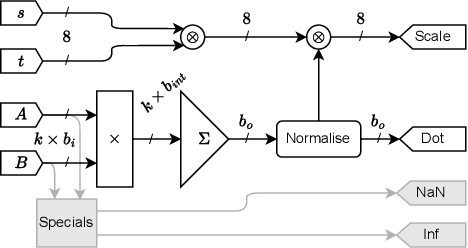
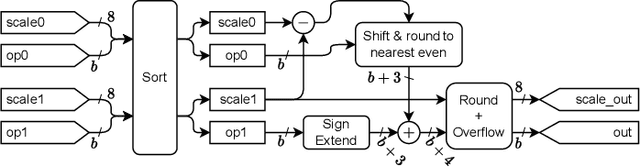
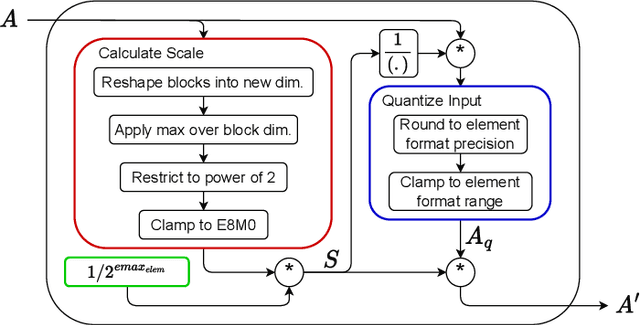
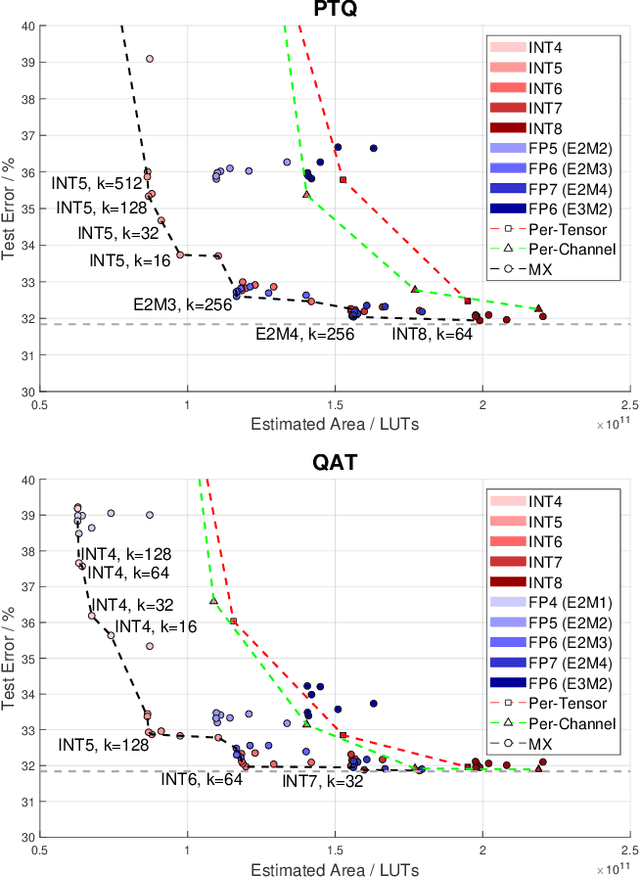
A number of companies recently worked together to release the new Open Compute Project MX standard for low-precision computation, aimed at efficient neural network implementation. In this paper, we describe and evaluate the first open-source FPGA implementation of the arithmetic defined in the standard. Our designs fully support all the standard's concrete formats for conversion into and out of MX formats and for the standard-defined arithmetic operations, as well as arbitrary fixed-point and floating-point formats. Certain elements of the standard are left as implementation-defined, and we present the first concrete FPGA-inspired choices for these elements, which we outline in the paper. Our library of optimized hardware components is available open source, and can be used to build larger systems. For this purpose, we also describe and release an open-source Pytorch library for quantization into the new standard, integrated with the Brevitas library so that the community can develop novel neural network designs quantized with MX formats in mind. We demonstrate the usability and efficacy of our libraries via the implementation of example neural networks such as ResNet-18 on the ImageNet ILSVRC12 dataset. Our testing shows that MX is very effective for formats such as INT5 or FP6 which are not natively supported on GPUs. This gives FPGAs an advantage as they have the flexibility to implement a custom datapath and take advantage of the smaller area footprints offered by these formats.

Optimised Grouped-Query Attention Mechanism for Transformers

Grouped-query attention (GQA) has been widely adopted in LLMs to mitigate the complexity of multi-head attention (MHA). To transform an MHA to a GQA, neighbour queries in MHA are evenly split into groups where each group shares the value and key layers. In this work, we propose AsymGQA, an activation-informed approach to asymmetrically grouping an MHA to a GQA for better model performance. Our AsymGQA outperforms the GQA within the same model size budget. For example, AsymGQA LLaMA-2-7B has an accuracy increase of 7.5% on MMLU compared to neighbour grouping. Our approach addresses the GQA's trade-off problem between model performance and hardware efficiency.

Unlocking the Global Synergies in Low-Rank Adapters

Low-rank Adaption (LoRA) has been the de-facto parameter-efficient fine-tuning technique for large language models. We present HeteroLoRA, a light-weight search algorithm that leverages zero-cost proxies to allocate the limited LoRA trainable parameters across the model for better fine-tuned performance. In addition to the allocation for the standard LoRA-adapted models, we also demonstrate the efficacy of HeteroLoRA by performing the allocation in a more challenging search space that includes LoRA modules and LoRA-adapted shortcut connections. Experiments show that HeteroLoRA enables improvements in model performance given the same parameter budge. For example, on MRPC, we see an improvement of 1.6% in accuracy with similar training parameter budget. We will open-source our algorithm once the paper is accepted.

NeuraLUT: Hiding Neural Network Density in Boolean Synthesizable Functions

Field-Programmable Gate Array (FPGA) accelerators have proven successful in handling latency- and resource-critical deep neural network (DNN) inference tasks. Among the most computationally intensive operations in a neural network (NN) is the dot product between the feature and weight vectors. Thus, some previous FPGA acceleration works have proposed mapping neurons with quantized inputs and outputs directly to lookup tables (LUTs) for hardware implementation. In these works, the boundaries of the neurons coincide with the boundaries of the LUTs. We propose relaxing these boundaries and mapping entire sub-networks to a single LUT. As the sub-networks are absorbed within the LUT, the NN topology and precision within a partition do not affect the size of the lookup tables generated. Therefore, we utilize fully connected layers with floating-point precision inside each partition, which benefit from being universal function approximators, with rigid sparsity and quantization enforced only between partitions, where the NN topology becomes exposed to the circuit topology. Although cheap to implement, this approach can lead to very deep NNs, and so to tackle challenges like vanishing gradients, we also introduce skip connections inside the partitions. The resulting methodology can be seen as training DNNs with a specific sparsity pattern that allows them to be mapped to much shallower circuit-level networks, thereby significantly improving latency. We validate our proposed method on a known latency-critical task, jet substructure tagging, and on the classical computer vision task, the digit classification using MNIST. Our approach allows for greater function expressivity within the LUTs compared to existing work, leading to lower latency NNs for the same accuracy.

LQER: Low-Rank Quantization Error Reconstruction for LLMs

Post-training quantization of Large Language Models (LLMs) is challenging. In this work, we introduce Low-rank Quantization Error Reduction (LQER), which combines quantization and low-rank approximation to recover the model capability. LQER leverages an activation-induced scale matrix to drive the singular value distribution of quantization error towards a desirable distribution, which enables nearly-lossless W4A8 quantization on various LLMs and downstream tasks without the need for knowledge distillation, grid search, or gradient-base iterative optimization. Unlike existing methods, the computation pattern of LQER eliminates the need for specialized Scatter and Gather processes to collect high-precision weights from irregular memory locations. Our W4A8 LLMs achieve near-lossless performance on six popular downstream tasks, while using 1.36$\times$ fewer hardware resources than the leading state-of-the-art method. We will open-source our framework once the paper is accepted.

Revisiting Block-based Quantisation: What is Important for Sub-8-bit LLM Inference?

The inference of Large language models (LLMs) requires immense computation and memory resources. To curtail these costs, quantisation has merged as a promising solution, but existing LLM quantisation mainly focuses on 8-bit. In this work, we explore the statistical and learning properties of the LLM layer and attribute the bottleneck of LLM quantisation to numerical scaling offsets. To address this, we adapt block quantisations for LLMs, a family of methods that share scaling factors across packed numbers. Block quantisations efficiently reduce the numerical scaling offsets solely from an arithmetic perspective, without additional treatments in the computational path. Our nearly-lossless quantised 6-bit LLMs achieve a $19\times$ higher arithmetic density and $5\times$ memory density than the float32 baseline, surpassing the prior art 8-bit quantisation by $2.5\times$ in arithmetic density and $1.2\times$ in memory density, without requiring any data calibration or re-training. We also share our insights into sub-8-bit LLM quantisation, including the mismatch between activation and weight distributions, optimal fine-tuning strategies, and a lower quantisation granularity inherent in the statistical properties of LLMs. The latter two tricks enable nearly-lossless 4-bit LLMs on downstream tasks. Our code is open-sourced.