A3 : an Analytical Low-Rank Approximation Framework for Attention

Large language models have demonstrated remarkable performance; however, their massive parameter counts make deployment highly expensive. Low-rank approximation offers a promising compression solution, yet existing approaches have two main limitations: (1) They focus on minimizing the output error of individual linear layers, without considering the architectural characteristics of Transformers, and (2) they decompose a large weight matrix into two small low-rank matrices. Consequently, these methods often fall short compared to other compression techniques like pruning and quantization, and introduce runtime overhead such as the extra GEMM kernel launches for decomposed small matrices. To address these limitations, we propose $\tt A^\tt 3$, a post-training low-rank approximation framework. $\tt A^\tt 3$ splits a Transformer layer into three functional components, namely $\tt QK$, $\tt OV$, and $\tt MLP$. For each component, $\tt A^\tt 3$ provides an analytical solution that reduces the hidden dimension size inside each component while minimizing the component's functional loss ($\it i.e.$, error in attention scores, attention outputs, and MLP outputs). This approach directly reduces model sizes, KV cache sizes, and FLOPs without introducing any runtime overheads. In addition, it provides a new narrative in advancing the optimization problem from singular linear layer loss optimization toward improved end-to-end performance. Through extensive experiments, we show that $\tt A^\tt 3$ maintains superior performance compared to SoTAs. For example, under the same reduction budget in computation and memory, our low-rank approximated LLaMA 3.1-70B achieves a perplexity of 4.69 on WikiText-2, outperforming the previous SoTA's 7.87 by 3.18. We also demonstrate the versatility of $\tt A^\tt 3$, including KV cache compression, quantization, and mixed-rank assignments for enhanced performance.

ARIES: Autonomous Reasoning with LLMs on Interactive Thought Graph Environments

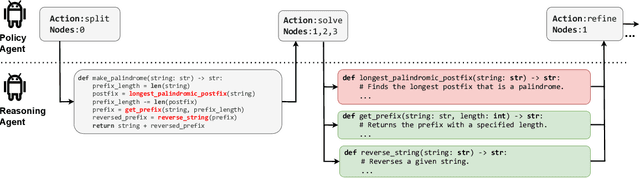
Recent research has shown that LLM performance on reasoning tasks can be enhanced by scaling test-time compute. One promising approach, particularly with decomposable problems, involves arranging intermediate solutions as a graph on which transformations are performed to explore the solution space. However, prior works rely on pre-determined, task-specific transformation schedules which are subject to a set of searched hyperparameters. In this work, we view thought graph transformations as actions in a Markov decision process, and implement policy agents to drive effective action policies for the underlying reasoning LLM agent. In particular, we investigate the ability for another LLM to act as a policy agent on thought graph environments and introduce ARIES, a multi-agent architecture for reasoning with LLMs. In ARIES, reasoning LLM agents solve decomposed subproblems, while policy LLM agents maintain visibility of the thought graph states, and dynamically adapt the problem-solving strategy. Through extensive experiments, we observe that using off-the-shelf LLMs as policy agents with no supervised fine-tuning (SFT) can yield up to $29\%$ higher accuracy on HumanEval relative to static transformation schedules, as well as reducing inference costs by $35\%$ and avoid any search requirements. We also conduct a thorough analysis of observed failure modes, highlighting that limitations on LLM sizes and the depth of problem decomposition can be seen as challenges to scaling LLM-guided reasoning.

AMPLE: Event-Driven Accelerator for Mixed-Precision Inference of Graph Neural Networks

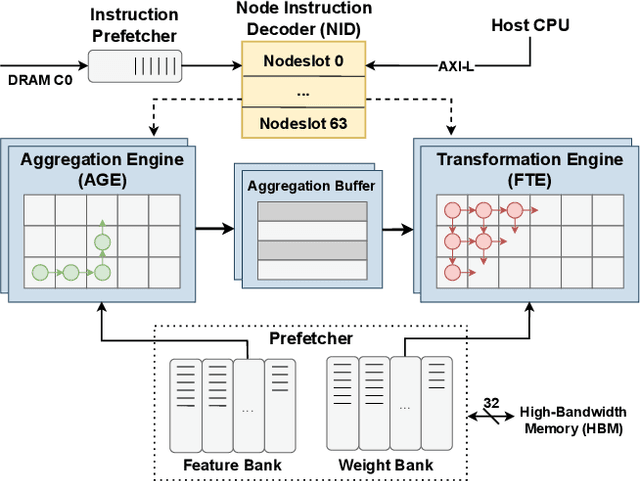
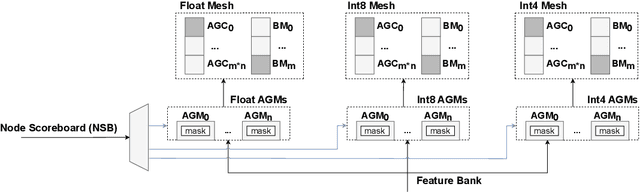
Graph Neural Networks (GNNs) have recently gained attention due to their performance on non-Euclidean data. The use of custom hardware architectures proves particularly beneficial for GNNs due to their irregular memory access patterns, resulting from the sparse structure of graphs. However, existing FPGA accelerators are limited by their double buffering mechanism, which doesn't account for the irregular node distribution in typical graph datasets. To address this, we introduce \textbf{AMPLE} (Accelerated Message Passing Logic Engine), an FPGA accelerator leveraging a new event-driven programming flow. We develop a mixed-arithmetic architecture, enabling GNN inference to be quantized at a node-level granularity. Finally, prefetcher for data and instructions is implemented to optimize off-chip memory access and maximize node parallelism. Evaluation on citation and social media graph datasets ranging from $2$K to $700$K nodes showed a mean speedup of $243\times$ and $7.2\times$ against CPU and GPU counterparts, respectively.

Scaling Laws for Mixed quantization in Large Language Models

Post-training quantization of Large Language Models (LLMs) has proven effective in reducing the computational requirements for running inference on these models. In this study, we focus on a straightforward question: When aiming for a specific accuracy or perplexity target for low-precision quantization, how many high-precision numbers or calculations are required to preserve as we scale LLMs to larger sizes? We first introduce a critical metric named the quantization ratio, which compares the number of parameters quantized to low-precision arithmetic against the total parameter count. Through extensive and carefully controlled experiments across different model families, arithmetic types, and quantization granularities (e.g. layer-wise, matmul-wise), we identify two central phenomenons. 1) The larger the models, the better they can preserve performance with an increased quantization ratio, as measured by perplexity in pre-training tasks or accuracy in downstream tasks. 2) The finer the granularity of mixed-precision quantization (e.g., matmul-wise), the more the model can increase the quantization ratio. We believe these observed phenomena offer valuable insights for future AI hardware design and the development of advanced Efficient AI algorithms.