Detecting Concept Drift in the Presence of Sparsity -- A Case Study of Automated Change Risk Assessment System

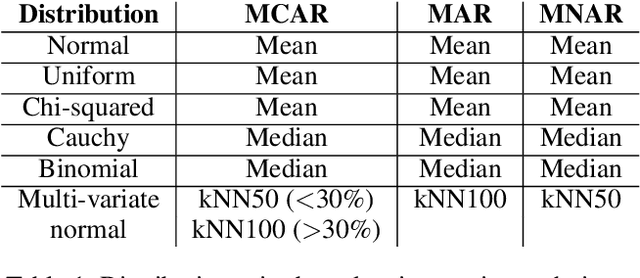
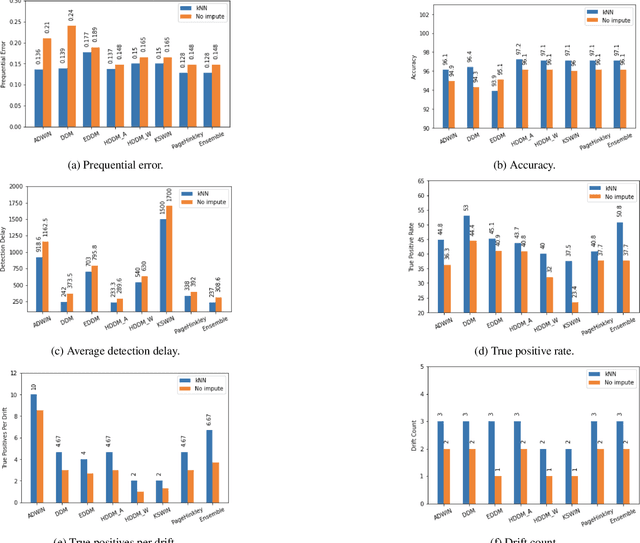
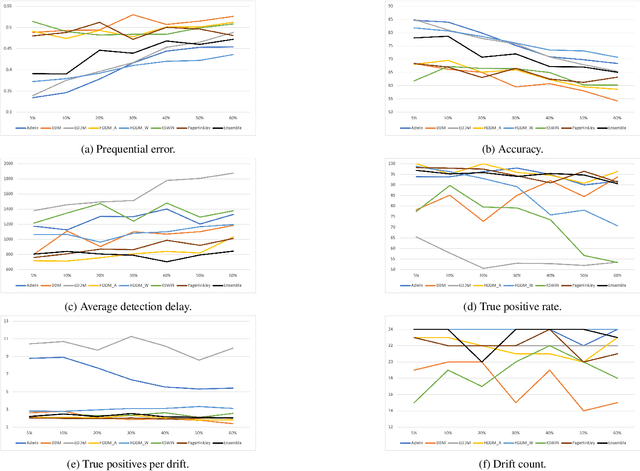
Missing values, widely called as \textit{sparsity} in literature, is a common characteristic of many real-world datasets. Many imputation methods have been proposed to address this problem of data incompleteness or sparsity. However, the accuracy of a data imputation method for a given feature or a set of features in a dataset is highly dependent on the distribution of the feature values and its correlation with other features. Another problem that plagues industry deployments of machine learning (ML) solutions is concept drift detection, which becomes more challenging in the presence of missing values. Although data imputation and concept drift detection have been studied extensively, little work has attempted a combined study of the two phenomena, i.e., concept drift detection in the presence of sparsity. In this work, we carry out a systematic study of the following: (i) different patterns of missing values, (ii) various statistical and ML based data imputation methods for different kinds of sparsity, (iii) several concept drift detection methods, (iv) practical analysis of the various drift detection metrics, (v) selecting the best concept drift detector given a dataset with missing values based on the different metrics. We first analyze it on synthetic data and publicly available datasets, and finally extend the findings to our deployed solution of automated change risk assessment system. One of the major findings from our empirical study is the absence of supremacy of any one concept drift detection method across all the relevant metrics. Therefore, we adopt a majority voting based ensemble of concept drift detectors for abrupt and gradual concept drifts. Our experiments show optimal or near optimal performance can be achieved for this ensemble method across all the metrics.

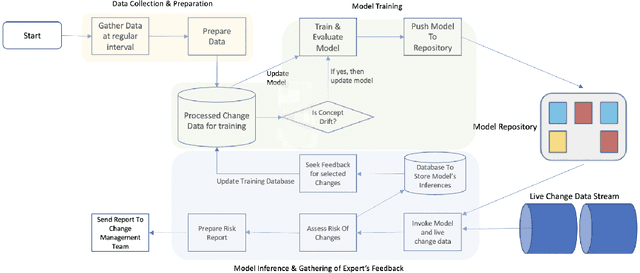
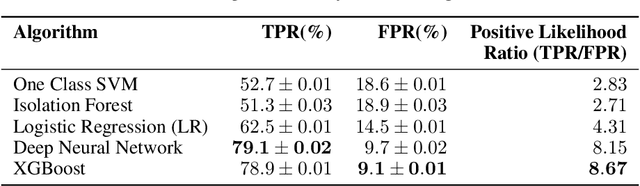
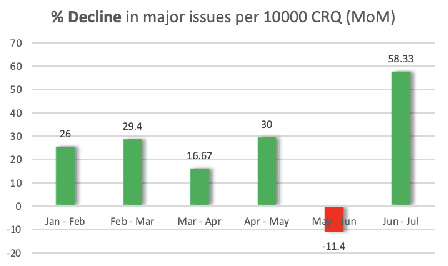
Look Before You Leap! Designing a Human-Centered AI System for Change Risk Assessment

Reducing the number of failures in a production system is one of the most challenging problems in technology driven industries, such as, the online retail industry. To address this challenge, change management has emerged as a promising sub-field in operations that manages and reviews the changes to be deployed in production in a systematic manner. However, it is practically impossible to manually review a large number of changes on a daily basis and assess the risk associated with them. This warrants the development of an automated system to assess the risk associated with a large number of changes. There are a few commercial solutions available to address this problem but those solutions lack the ability to incorporate domain knowledge and continuous feedback from domain experts into the risk assessment process. As part of this work, we aim to bridge the gap between model-driven risk assessment of change requests and the assessment of domain experts by building a continuous feedback loop into the risk assessment process. Here we present our work to build an end-to-end machine learning system along with the discussion of some of practical challenges we faced related to extreme skewness in class distribution, concept drift, estimation of the uncertainty associated with the model's prediction and the overall scalability of the system.

Exploring Alternatives to Softmax Function

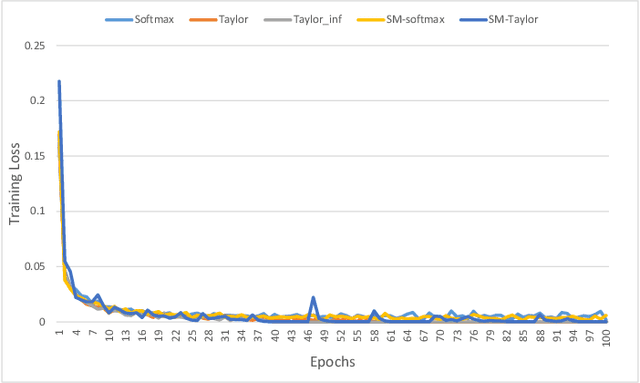
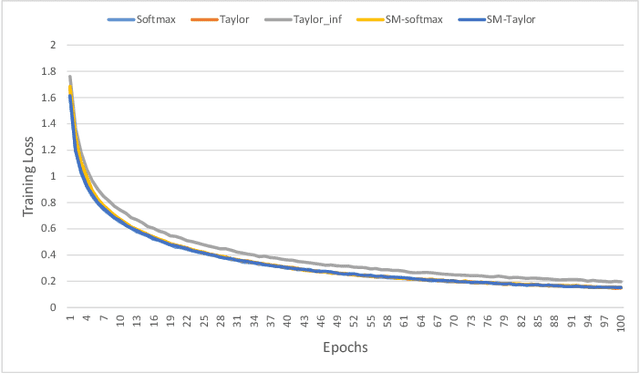
Softmax function is widely used in artificial neural networks for multiclass classification, multilabel classification, attention mechanisms, etc. However, its efficacy is often questioned in literature. The log-softmax loss has been shown to belong to a more generic class of loss functions, called spherical family, and its member log-Taylor softmax loss is arguably the best alternative in this class. In another approach which tries to enhance the discriminative nature of the softmax function, soft-margin softmax (SM-softmax) has been proposed to be the most suitable alternative. In this work, we investigate Taylor softmax, SM-softmax and our proposed SM-Taylor softmax, an amalgamation of the earlier two functions, as alternatives to softmax function. Furthermore, we explore the effect of expanding Taylor softmax up to ten terms (original work proposed expanding only to two terms) along with the ramifications of considering Taylor softmax to be a finite or infinite series during backpropagation. Our experiments for the image classification task on different datasets reveal that there is always a configuration of the SM-Taylor softmax function that outperforms the normal softmax function and its other alternatives.

K-TanH: Hardware Efficient Activations For Deep Learning

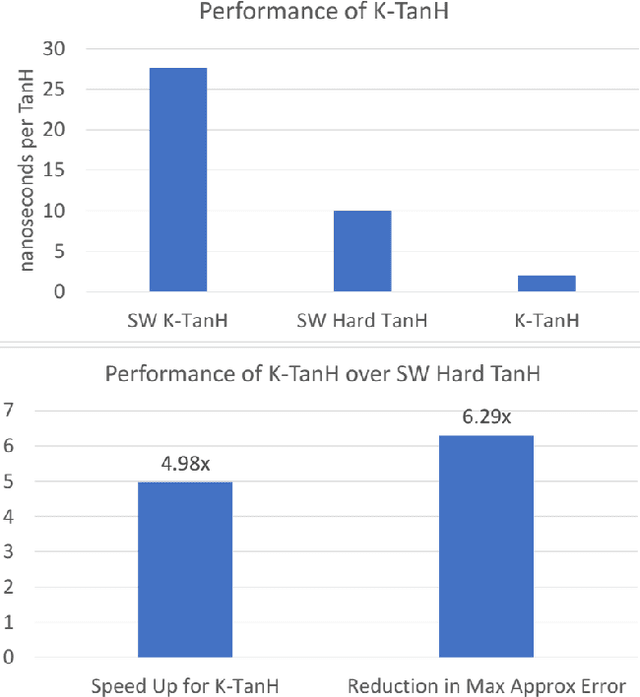
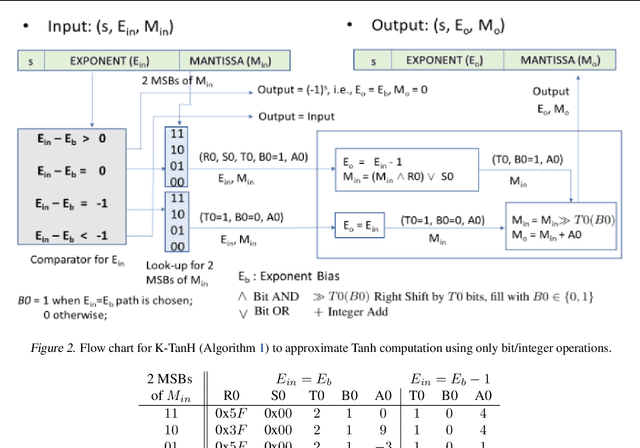
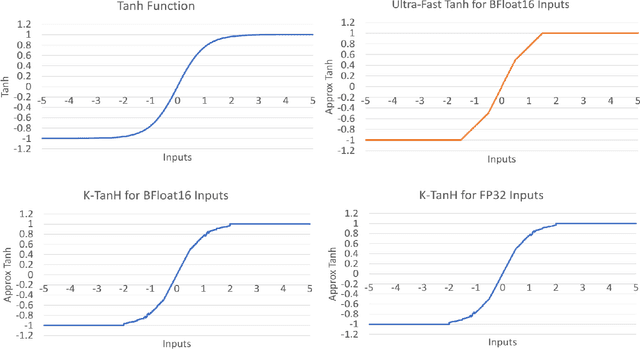
We propose K-TanH, a novel, highly accurate, hardware efficient approximation of popular activation function Tanh for Deep Learning. K-TanH consists of a sequence of parameterized bit/integer operations, such as, masking, shift and add/subtract (no floating point operation needed) where parameters are stored in a very small look-up table (bit-masking step can be eliminated). The design of K-TanH is flexible enough to deal with multiple numerical formats, such as, FP32 and BFloat16. High quality approximations to other activation functions, e.g., Swish and GELU, can be derived from K-TanH. We provide RTL design for K-TanH to demonstrate its area/power/performance efficacy. It is more accurate than existing piecewise approximations for Tanh. For example, K-TanH achieves $\sim 5\times$ speed up and $> 6\times$ reduction in maximum approximation error over software implementation of Hard TanH. Experimental results for low-precision BFloat16 training of language translation model GNMT on WMT16 data sets with approximate Tanh and Sigmoid obtained via K-TanH achieve similar accuracy and convergence as training with exact Tanh and Sigmoid.

High-Performance Deep Learning via a Single Building Block

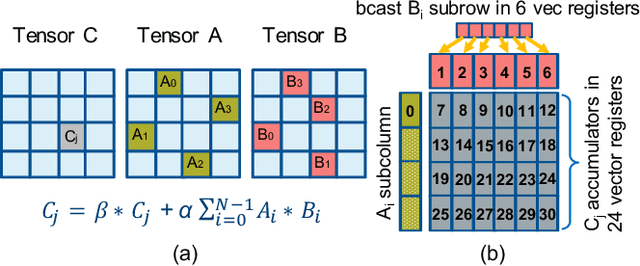
Deep learning (DL) is one of the most prominent branches of machine learning. Due to the immense computational cost of DL workloads, industry and academia have developed DL libraries with highly-specialized kernels for each workload/architecture, leading to numerous, complex code-bases that strive for performance, yet they are hard to maintain and do not generalize. In this work, we introduce the batch-reduce GEMM kernel and show how the most popular DL algorithms can be formulated with this kernel as the basic building-block. Consequently, the DL library-development degenerates to mere (potentially automatic) tuning of loops around this sole optimized kernel. By exploiting our new kernel we implement Recurrent Neural Networks, Convolution Neural Networks and Multilayer Perceptron training and inference primitives in just 3K lines of high-level code. Our primitives outperform vendor-optimized libraries on multi-node CPU clusters, and we also provide proof-of-concept CNN kernels targeting GPUs. Finally, we demonstrate that the batch-reduce GEMM kernel within a tensor compiler yields high-performance CNN primitives, further amplifying the viability of our approach.

A Study of BFLOAT16 for Deep Learning Training

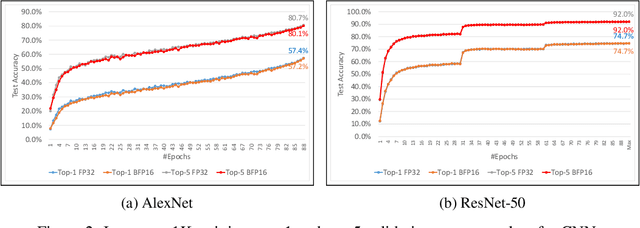
This paper presents the first comprehensive empirical study demonstrating the efficacy of the Brain Floating Point (BFLOAT16) half-precision format for Deep Learning training across image classification, speech recognition, language modeling, generative networks and industrial recommendation systems. BFLOAT16 is attractive for Deep Learning training for two reasons: the range of values it can represent is the same as that of IEEE 754 floating-point format (FP32) and conversion to/from FP32 is simple. Maintaining the same range as FP32 is important to ensure that no hyper-parameter tuning is required for convergence; e.g., IEEE 754 compliant half-precision floating point (FP16) requires hyper-parameter tuning. In this paper, we discuss the flow of tensors and various key operations in mixed precision training, and delve into details of operations, such as the rounding modes for converting FP32 tensors to BFLOAT16. We have implemented a method to emulate BFLOAT16 operations in Tensorflow, Caffe2, IntelCaffe, and Neon for our experiments. Our results show that deep learning training using BFLOAT16 tensors achieves the same state-of-the-art (SOTA) results across domains as FP32 tensors in the same number of iterations and with no changes to hyper-parameters.

Mixed Precision Training of Convolutional Neural Networks using Integer Operations

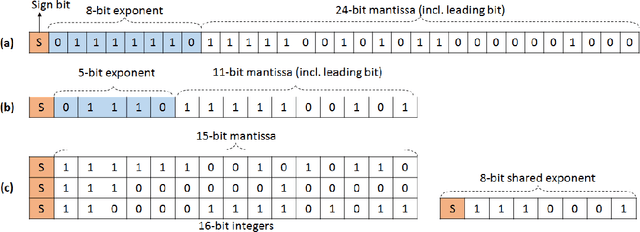
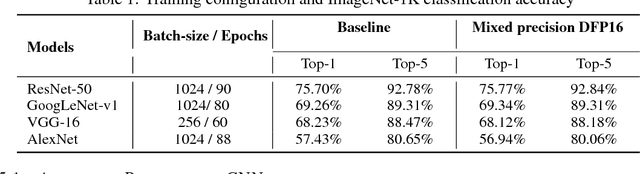
The state-of-the-art (SOTA) for mixed precision training is dominated by variants of low precision floating point operations, and in particular, FP16 accumulating into FP32 Micikevicius et al. (2017). On the other hand, while a lot of research has also happened in the domain of low and mixed-precision Integer training, these works either present results for non-SOTA networks (for instance only AlexNet for ImageNet-1K), or relatively small datasets (like CIFAR-10). In this work, we train state-of-the-art visual understanding neural networks on the ImageNet-1K dataset, with Integer operations on General Purpose (GP) hardware. In particular, we focus on Integer Fused-Multiply-and-Accumulate (FMA) operations which take two pairs of INT16 operands and accumulate results into an INT32 output.We propose a shared exponent representation of tensors and develop a Dynamic Fixed Point (DFP) scheme suitable for common neural network operations. The nuances of developing an efficient integer convolution kernel is examined, including methods to handle overflow of the INT32 accumulator. We implement CNN training for ResNet-50, GoogLeNet-v1, VGG-16 and AlexNet; and these networks achieve or exceed SOTA accuracy within the same number of iterations as their FP32 counterparts without any change in hyper-parameters and with a 1.8X improvement in end-to-end training throughput. To the best of our knowledge these results represent the first INT16 training results on GP hardware for ImageNet-1K dataset using SOTA CNNs and achieve highest reported accuracy using half-precision

Ternary Residual Networks

Sub-8-bit representation of DNNs incur some discernible loss of accuracy despite rigorous (re)training at low-precision. Such loss of accuracy essentially makes them equivalent to a much shallower counterpart, diminishing the power of being deep networks. To address this problem of accuracy drop we introduce the notion of \textit{residual networks} where we add more low-precision edges to sensitive branches of the sub-8-bit network to compensate for the lost accuracy. Further, we present a perturbation theory to identify such sensitive edges. Aided by such an elegant trade-off between accuracy and compute, the 8-2 model (8-bit activations, ternary weights), enhanced by ternary residual edges, turns out to be sophisticated enough to achieve very high accuracy ($\sim 1\%$ drop from our FP-32 baseline), despite $\sim 1.6\times$ reduction in model size, $\sim 26\times$ reduction in number of multiplications, and potentially $\sim 2\times$ power-performance gain comparing to 8-8 representation, on the state-of-the-art deep network ResNet-101 pre-trained on ImageNet dataset. Moreover, depending on the varying accuracy requirements in a dynamic environment, the deployed low-precision model can be upgraded/downgraded on-the-fly by partially enabling/disabling residual connections. For example, disabling the least important residual connections in the above enhanced network, the accuracy drop is $\sim 2\%$ (from FP32), despite $\sim 1.9\times$ reduction in model size, $\sim 32\times$ reduction in number of multiplications, and potentially $\sim 2.3\times$ power-performance gain comparing to 8-8 representation. Finally, all the ternary connections are sparse in nature, and the ternary residual conversion can be done in a resource-constraint setting with no low-precision (re)training.