Exploring Alternatives to Softmax Function
Paper and Code
Nov 23, 2020
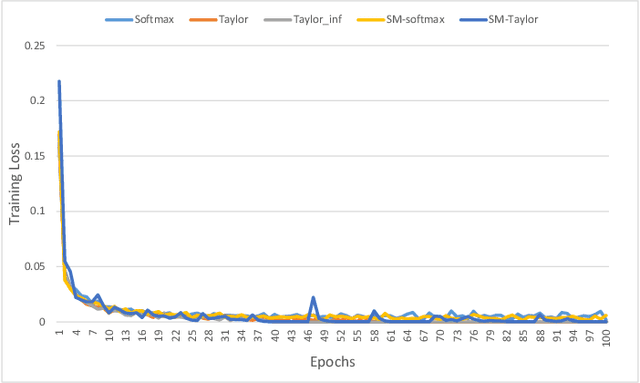

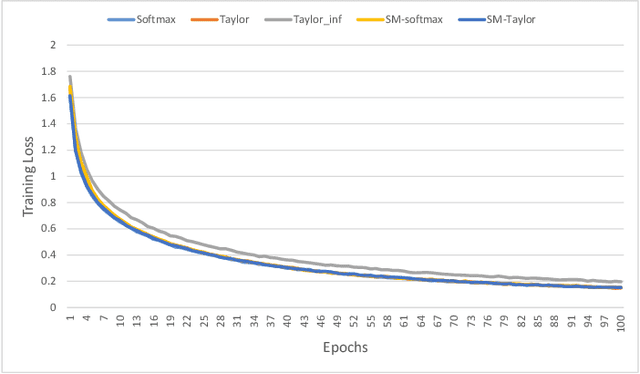
Softmax function is widely used in artificial neural networks for multiclass classification, multilabel classification, attention mechanisms, etc. However, its efficacy is often questioned in literature. The log-softmax loss has been shown to belong to a more generic class of loss functions, called spherical family, and its member log-Taylor softmax loss is arguably the best alternative in this class. In another approach which tries to enhance the discriminative nature of the softmax function, soft-margin softmax (SM-softmax) has been proposed to be the most suitable alternative. In this work, we investigate Taylor softmax, SM-softmax and our proposed SM-Taylor softmax, an amalgamation of the earlier two functions, as alternatives to softmax function. Furthermore, we explore the effect of expanding Taylor softmax up to ten terms (original work proposed expanding only to two terms) along with the ramifications of considering Taylor softmax to be a finite or infinite series during backpropagation. Our experiments for the image classification task on different datasets reveal that there is always a configuration of the SM-Taylor softmax function that outperforms the normal softmax function and its other alternatives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge