When Do Neural Nets Outperform Boosted Trees on Tabular Data?

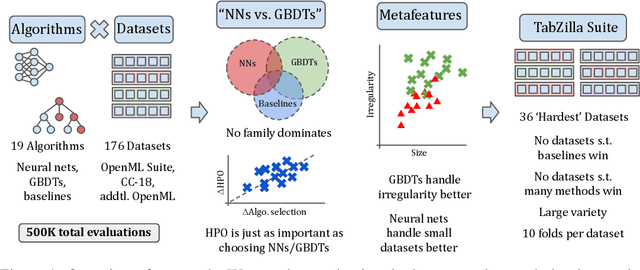
Tabular data is one of the most commonly used types of data in machine learning. Despite recent advances in neural nets (NNs) for tabular data, there is still an active discussion on whether or not NNs generally outperform gradient-boosted decision trees (GBDTs) on tabular data, with several recent works arguing either that GBDTs consistently outperform NNs on tabular data, or vice versa. In this work, we take a step back and ask, 'does it matter?' We conduct the largest tabular data analysis to date, by comparing 19 algorithms across 176 datasets, and we find that the 'NN vs. GBDT' debate is overemphasized: for a surprisingly high number of datasets, either the performance difference between GBDTs and NNs is negligible, or light hyperparameter tuning on a GBDT is more important than selecting the best algorithm. Next, we analyze 965 metafeatures to determine what properties of a dataset make NNs or GBDTs better-suited to perform well. For example, we find that GBDTs are much better than NNs at handling skewed feature distributions, heavy-tailed feature distributions, and other forms of dataset irregularities. Our insights act as a guide for practitioners to decide whether or not they need to run a neural net to reach top performance on their dataset. Our codebase and all raw results are available at https://github.com/naszilla/tabzilla.

Speeding up NAS with Adaptive Subset Selection

A majority of recent developments in neural architecture search (NAS) have been aimed at decreasing the computational cost of various techniques without affecting their final performance. Towards this goal, several low-fidelity and performance prediction methods have been considered, including those that train only on subsets of the training data. In this work, we present an adaptive subset selection approach to NAS and present it as complementary to state-of-the-art NAS approaches. We uncover a natural connection between one-shot NAS algorithms and adaptive subset selection and devise an algorithm that makes use of state-of-the-art techniques from both areas. We use these techniques to substantially reduce the runtime of DARTS-PT (a leading one-shot NAS algorithm), as well as BOHB and DEHB (leading multifidelity optimization algorithms), without sacrificing accuracy. Our results are consistent across multiple datasets, and towards full reproducibility, we release our code at https: //anonymous.4open.science/r/SubsetSelection NAS-B132.

Exploring Alternatives to Softmax Function

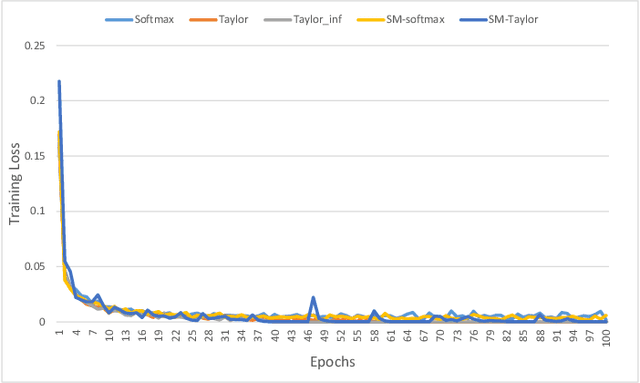
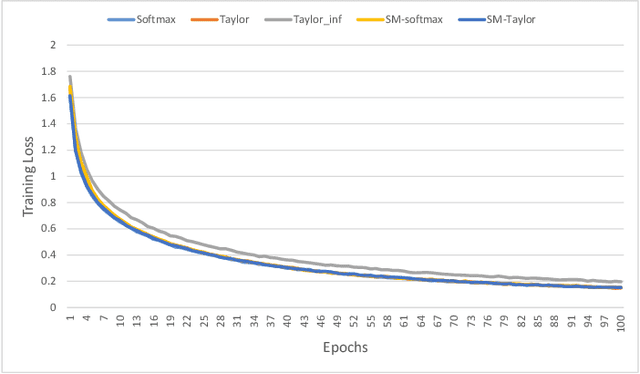
Softmax function is widely used in artificial neural networks for multiclass classification, multilabel classification, attention mechanisms, etc. However, its efficacy is often questioned in literature. The log-softmax loss has been shown to belong to a more generic class of loss functions, called spherical family, and its member log-Taylor softmax loss is arguably the best alternative in this class. In another approach which tries to enhance the discriminative nature of the softmax function, soft-margin softmax (SM-softmax) has been proposed to be the most suitable alternative. In this work, we investigate Taylor softmax, SM-softmax and our proposed SM-Taylor softmax, an amalgamation of the earlier two functions, as alternatives to softmax function. Furthermore, we explore the effect of expanding Taylor softmax up to ten terms (original work proposed expanding only to two terms) along with the ramifications of considering Taylor softmax to be a finite or infinite series during backpropagation. Our experiments for the image classification task on different datasets reveal that there is always a configuration of the SM-Taylor softmax function that outperforms the normal softmax function and its other alternatives.