George Pisha
Across Scales \& Across Dimensions: Temporal Super-Resolution using Deep Internal Learning
Mar 19, 2020Abstract:When a very fast dynamic event is recorded with a low-framerate camera, the resulting video suffers from severe motion blur (due to exposure time) and motion aliasing (due to low sampling rate in time). True Temporal Super-Resolution (TSR) is more than just Temporal-Interpolation (increasing framerate). It can also recover new high temporal frequencies beyond the temporal Nyquist limit of the input video, thus resolving both motion-blur and motion-aliasing effects that temporal frame interpolation (as sophisticated as it maybe) cannot undo. In this paper we propose a "Deep Internal Learning" approach for true TSR. We train a video-specific CNN on examples extracted directly from the low-framerate input video. Our method exploits the strong recurrence of small space-time patches inside a single video sequence, both within and across different spatio-temporal scales of the video. We further observe (for the first time) that small space-time patches recur also across-dimensions of the video sequence - i.e., by swapping the spatial and temporal dimensions. In particular, the higher spatial resolution of video frames provides strong examples as to how to increase the temporal resolution of that video. Such internal video-specific examples give rise to strong self-supervision, requiring no data but the input video itself. This results in Zero-Shot Temporal-SR of complex videos, which removes both motion blur and motion aliasing, outperforming previous supervised methods trained on external video datasets.
The Ramanujan Machine: Automatically Generated Conjectures on Fundamental Constants
Aug 03, 2019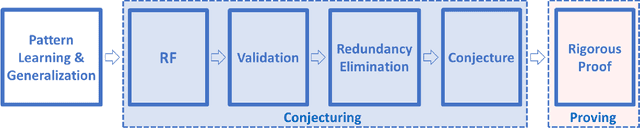



Abstract:Fundamental mathematical constants like $e$ and $\pi$ are ubiquitous in diverse fields of science, from abstract mathematics and geometry to physics, biology and chemistry. Nevertheless, for centuries new mathematical formulas relating fundamental constants have been scarce and usually discovered sporadically. In this paper we propose a novel and systematic approach that leverages algorithms for deriving mathematical formulas for fundamental constants and help reveal their underlying structure. Our algorithms find dozens of well-known as well as previously unknown continued fraction representations of $\pi$, $e$, and the Riemann zeta function values. Two conjectures produced by our algorithm, along with many others, are: \begin{equation*} \frac{e}{e-2} = 4 - \frac{1}{5-\frac{2}{6-\frac{3}{7-\frac{4}{8-\ldots}}}} \quad\quad,\quad\quad \frac{4}{3\pi-8} = 3-\frac{1\cdot1}{6-\frac{2\cdot3}{9-\frac{3\cdot5}{12-\frac{4\cdot 7}{15-\ldots}}}} \end{equation*} We present two algorithms that proved useful in finding conjectures: a variant of the Meet-In-The-Middle (MITM) algorithm and a Gradient Descent (GD) tailored to the recurrent structure of continued fractions. Both algorithms are based on matching numerical values and thus they conjecture formulas without providing proofs and without requiring any prior knowledge on any underlaying mathematical structure. This approach is especially attractive for fundamental constants for which no mathematical structure is known, as it reverses the conventional approach of sequential logic in formal proofs. Instead, our work supports a different conceptual approach for research: computer algorithms utilizing numerical data to unveil mathematical structures, thus trying to play the role of intuition of great mathematicians of the past, providing leads to new mathematical research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge