Accelerating Scientific Research with Gemini: Case Studies and Common Techniques

Recent advances in large language models (LLMs) have opened new avenues for accelerating scientific research. While models are increasingly capable of assisting with routine tasks, their ability to contribute to novel, expert-level mathematical discovery is less understood. We present a collection of case studies demonstrating how researchers have successfully collaborated with advanced AI models, specifically Google's Gemini-based models (in particular Gemini Deep Think and its advanced variants), to solve open problems, refute conjectures, and generate new proofs across diverse areas in theoretical computer science, as well as other areas such as economics, optimization, and physics. Based on these experiences, we extract common techniques for effective human-AI collaboration in theoretical research, such as iterative refinement, problem decomposition, and cross-disciplinary knowledge transfer. While the majority of our results stem from this interactive, conversational methodology, we also highlight specific instances that push beyond standard chat interfaces. These include deploying the model as a rigorous adversarial reviewer to detect subtle flaws in existing proofs, and embedding it within a "neuro-symbolic" loop that autonomously writes and executes code to verify complex derivations. Together, these examples highlight the potential of AI not just as a tool for automation, but as a versatile, genuine partner in the creative process of scientific discovery.

DeepCrossAttention: Supercharging Transformer Residual Connections

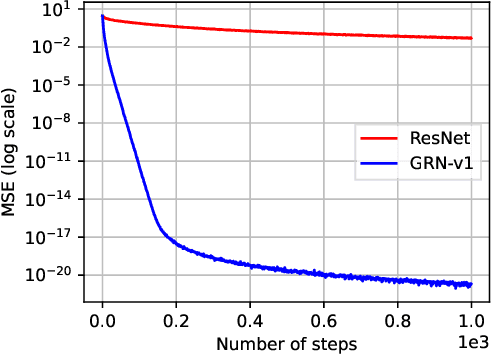
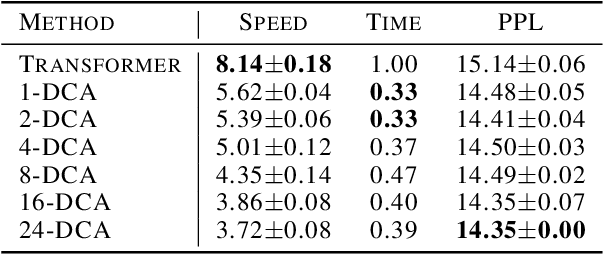
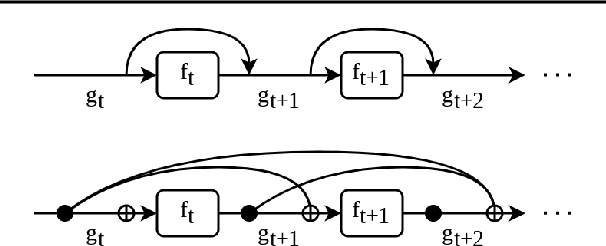
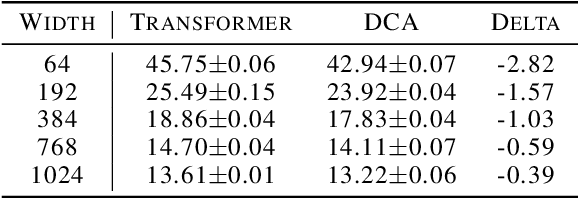
Transformer networks have achieved remarkable success across diverse domains, leveraging a variety of architectural innovations, including residual connections. However, traditional residual connections, which simply sum the outputs of previous layers, can dilute crucial information. This work introduces DeepCrossAttention (DCA), an approach that enhances residual learning in transformers. DCA employs learnable, input-dependent weights to dynamically combine layer outputs, enabling the model to selectively focus on the most relevant information in any of the previous layers. Furthermore, DCA incorporates depth-wise cross-attention, allowing for richer interactions between layers at different depths. Our language modeling experiments show that DCA achieves improved perplexity for a given training time. Moreover, DCA obtains the same model quality up to 3x faster while adding a negligible number of parameters. Theoretical analysis confirms that DCA provides an improved trade-off between accuracy and model size when the ratio of collective layer ranks to the ambient dimension falls below a critical threshold.

SequentialAttention++ for Block Sparsification: Differentiable Pruning Meets Combinatorial Optimization

Neural network pruning is a key technique towards engineering large yet scalable, interpretable, and generalizable models. Prior work on the subject has developed largely along two orthogonal directions: (1) differentiable pruning for efficiently and accurately scoring the importance of parameters, and (2) combinatorial optimization for efficiently searching over the space of sparse models. We unite the two approaches, both theoretically and empirically, to produce a coherent framework for structured neural network pruning in which differentiable pruning guides combinatorial optimization algorithms to select the most important sparse set of parameters. Theoretically, we show how many existing differentiable pruning techniques can be understood as nonconvex regularization for group sparse optimization, and prove that for a wide class of nonconvex regularizers, the global optimum is unique, group-sparse, and provably yields an approximate solution to a sparse convex optimization problem. The resulting algorithm that we propose, SequentialAttention++, advances the state of the art in large-scale neural network block-wise pruning tasks on the ImageNet and Criteo datasets.

A Scalable Algorithm for Individually Fair K-means Clustering

We present a scalable algorithm for the individually fair ($p$, $k$)-clustering problem introduced by Jung et al. and Mahabadi et al. Given $n$ points $P$ in a metric space, let $\delta(x)$ for $x\in P$ be the radius of the smallest ball around $x$ containing at least $n / k$ points. A clustering is then called individually fair if it has centers within distance $\delta(x)$ of $x$ for each $x\in P$. While good approximation algorithms are known for this problem no efficient practical algorithms with good theoretical guarantees have been presented. We design the first fast local-search algorithm that runs in ~$O(nk^2)$ time and obtains a bicriteria $(O(1), 6)$ approximation. Then we show empirically that not only is our algorithm much faster than prior work, but it also produces lower-cost solutions.

Gemini: A Family of Highly Capable Multimodal Models

This report introduces a new family of multimodal models, Gemini, that exhibit remarkable capabilities across image, audio, video, and text understanding. The Gemini family consists of Ultra, Pro, and Nano sizes, suitable for applications ranging from complex reasoning tasks to on-device memory-constrained use-cases. Evaluation on a broad range of benchmarks shows that our most-capable Gemini Ultra model advances the state of the art in 30 of 32 of these benchmarks - notably being the first model to achieve human-expert performance on the well-studied exam benchmark MMLU, and improving the state of the art in every one of the 20 multimodal benchmarks we examined. We believe that the new capabilities of Gemini models in cross-modal reasoning and language understanding will enable a wide variety of use cases and we discuss our approach toward deploying them responsibly to users.

Agile Modeling: Image Classification with Domain Experts in the Loop

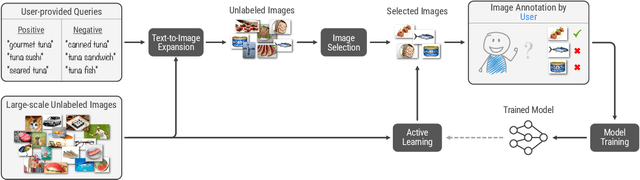
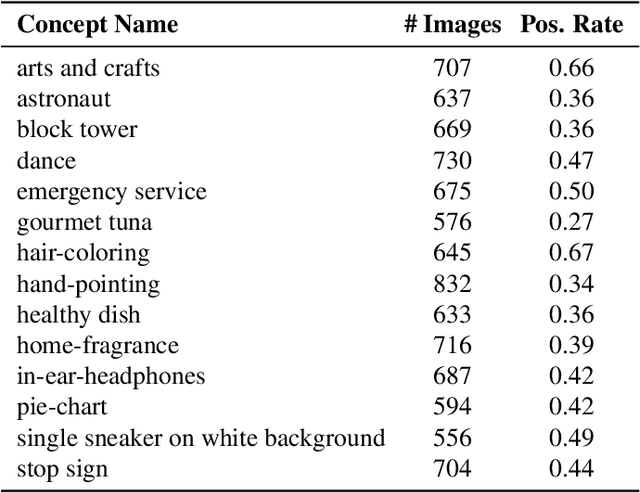
Machine learning is not readily accessible to domain experts from many fields, blocked by issues ranging from data mining to model training. We argue that domain experts should be at the center of the modeling process, and we introduce the "Agile Modeling" problem: the process of turning any visual concept from an idea into a well-trained ML classifier through a human-in-the-loop interaction driven by the domain expert in a way that minimizes domain expert time. We propose a solution to the problem that enables domain experts to create classifiers in real-time and build upon recent advances in image-text co-embeddings such as CLIP or ALIGN to implement it. We show the feasibility of this solution through live experiments with 14 domain experts, each modeling their own concept. Finally, we compare a domain expert driven process with the traditional crowdsourcing paradigm and find that difficult concepts see pronounced improvements with domain experts.

Sequential Attention for Feature Selection

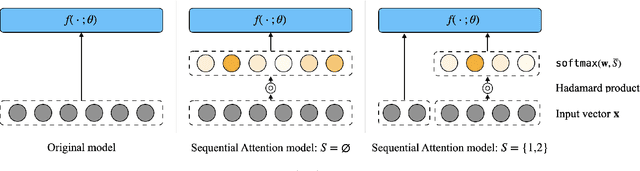
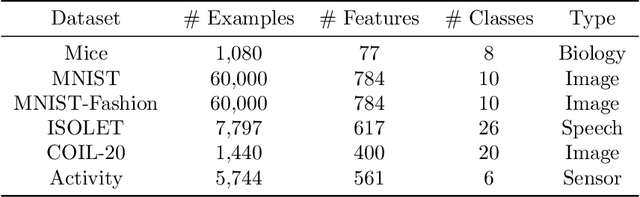
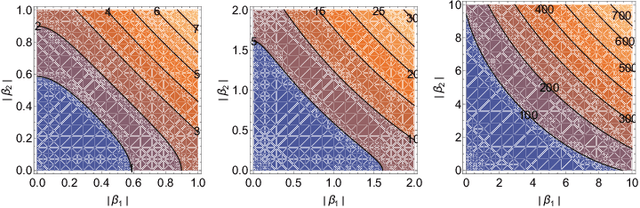
Feature selection is the problem of selecting a subset of features for a machine learning model that maximizes model quality subject to a resource budget constraint. For neural networks, prior methods, including those based on $\ell_1$ regularization, attention, and stochastic gates, typically select all of the features in one evaluation round, ignoring the residual value of the features during selection (i.e., the marginal contribution of a feature conditioned on the previously selected features). We propose a feature selection algorithm called Sequential Attention that achieves state-of-the-art empirical results for neural networks. This algorithm is based on an efficient implementation of greedy forward selection and uses attention weights at each step as a proxy for marginal feature importance. We provide theoretical insights into our Sequential Attention algorithm for linear regression models by showing that an adaptation to this setting is equivalent to the classical Orthogonal Matching Pursuit algorithm [PRK1993], and thus inherits all of its provable guarantees. Lastly, our theoretical and empirical analyses provide new explanations towards the effectiveness of attention and its connections to overparameterization, which might be of independent interest.

Tackling Provably Hard Representative Selection via Graph Neural Networks

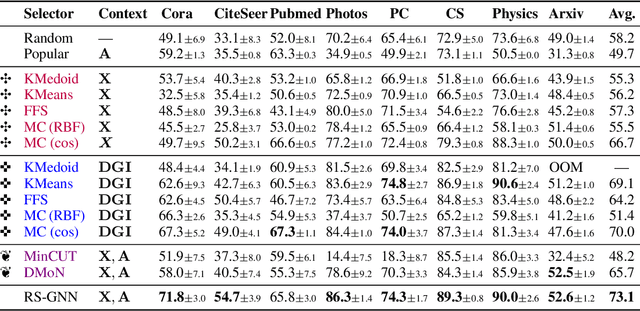
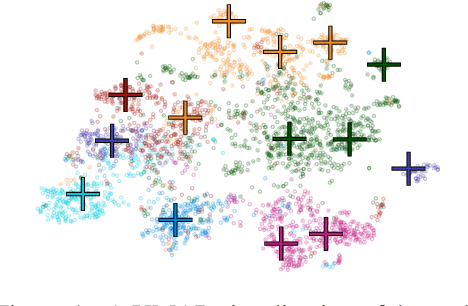
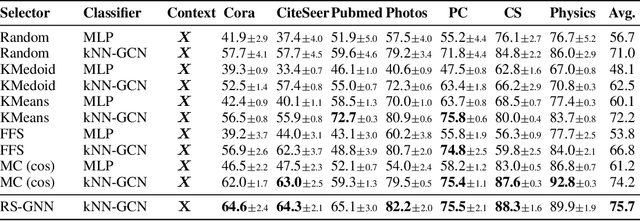
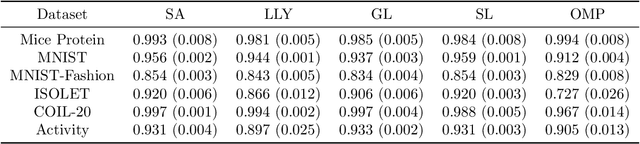
Representative selection (RS) is the problem of finding a small subset of exemplars from an unlabeled dataset, and has numerous applications in summarization, active learning, data compression and many other domains. In this paper, we focus on finding representatives that optimize the accuracy of a model trained on the selected representatives. We study RS for data represented as attributed graphs. We develop RS-GNN, a representation learning-based RS model based on Graph Neural Networks. Empirically, we demonstrate the effectiveness of RS-GNN on problems with predefined graph structures as well as problems with graphs induced from node feature similarities, by showing that RS-GNN achieves significant improvements over established baselines that optimize surrogate functions. Theoretically, we establish a new hardness result for RS by proving that RS is hard to approximate in polynomial time within any reasonable factor, which implies a significant gap between the optimum solution of widely-used surrogate functions and the actual accuracy of the model, and provides justification for the superiority of representation learning-based approaches such as RS-GNN over surrogate functions.

On Complexity of 1-Center in Various Metrics

We consider the classic 1-center problem: Given a set P of n points in a metric space find the point in P that minimizes the maximum distance to the other points of P. We study the complexity of this problem in d-dimensional $\ell_p$-metrics and in edit and Ulam metrics over strings of length d. Our results for the 1-center problem may be classified based on d as follows. $\bullet$ Small d: We provide the first linear-time algorithm for 1-center problem in fixed-dimensional $\ell_1$ metrics. On the other hand, assuming the hitting set conjecture (HSC), we show that when $d=\omega(\log n)$, no subquadratic algorithm can solve 1-center problem in any of the $\ell_p$-metrics, or in edit or Ulam metrics. $\bullet$ Large d. When $d=\Omega(n)$, we extend our conditional lower bound to rule out sub quartic algorithms for 1-center problem in edit metric (assuming Quantified SETH). On the other hand, we give a $(1+\epsilon)$-approximation for 1-center in Ulam metric with running time $\tilde{O_{\epsilon}}(nd+n^2\sqrt{d})$. We also strengthen some of the above lower bounds by allowing approximations or by reducing the dimension d, but only against a weaker class of algorithms which list all requisite solutions. Moreover, we extend one of our hardness results to rule out subquartic algorithms for the well-studied 1-median problem in the edit metric, where given a set of n strings each of length n, the goal is to find a string in the set that minimizes the sum of the edit distances to the rest of the strings in the set.

Streaming Belief Propagation for Community Detection

The community detection problem requires to cluster the nodes of a network into a small number of well-connected "communities". There has been substantial recent progress in characterizing the fundamental statistical limits of community detection under simple stochastic block models. However, in real-world applications, the network structure is typically dynamic, with nodes that join over time. In this setting, we would like a detection algorithm to perform only a limited number of updates at each node arrival. While standard voting approaches satisfy this constraint, it is unclear whether they exploit the network information optimally. We introduce a simple model for networks growing over time which we refer to as streaming stochastic block model (StSBM). Within this model, we prove that voting algorithms have fundamental limitations. We also develop a streaming belief-propagation (StreamBP) approach, for which we prove optimality in certain regimes. We validate our theoretical findings on synthetic and real data.