Subquadratic Kronecker Regression with Applications to Tensor Decomposition

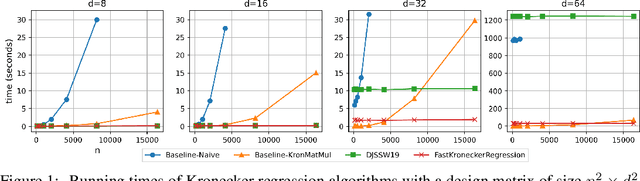
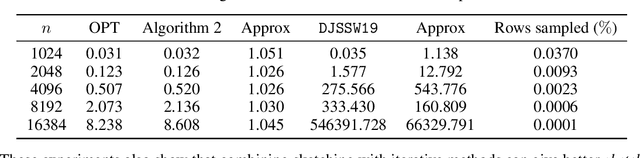
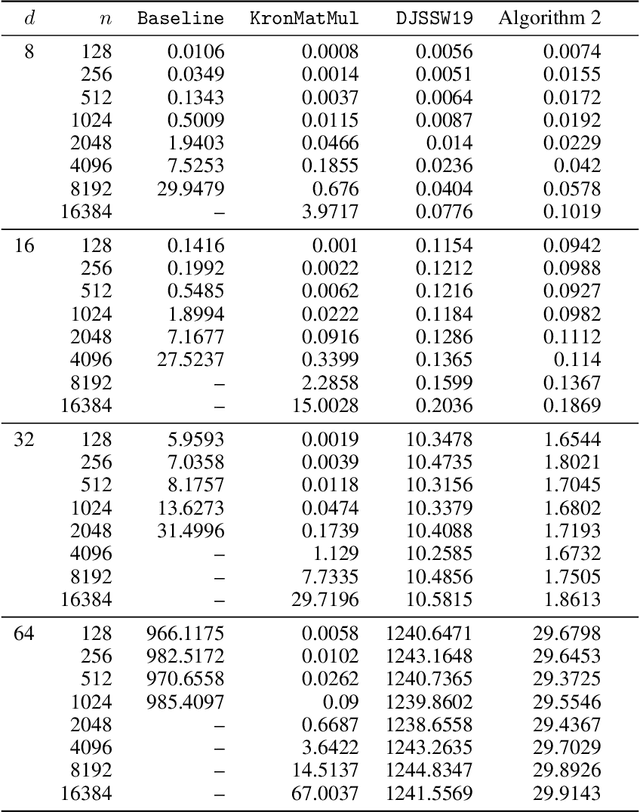
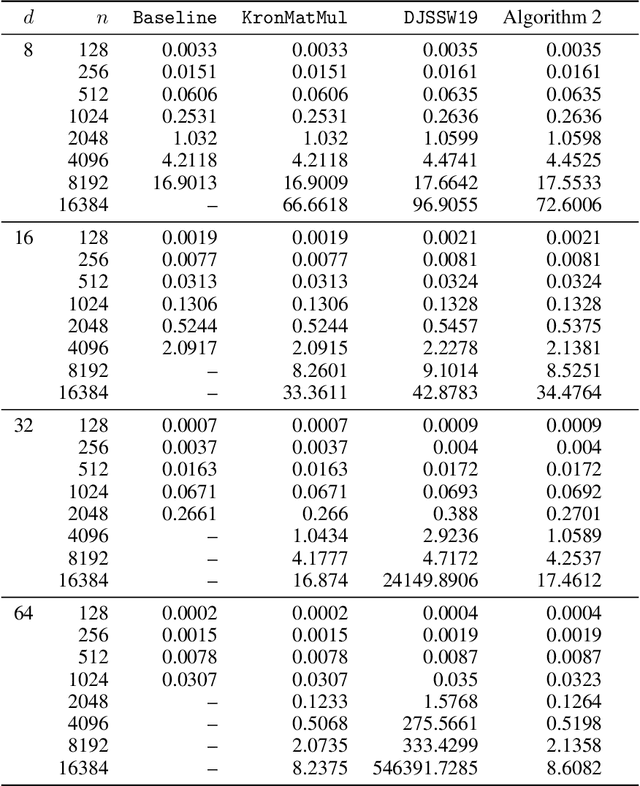
Kronecker regression is a highly-structured least squares problem $\min_{\mathbf{x}} \lVert \mathbf{K}\mathbf{x} - \mathbf{b} \rVert_{2}^2$, where the design matrix $\mathbf{K} = \mathbf{A}^{(1)} \otimes \cdots \otimes \mathbf{A}^{(N)}$ is a Kronecker product of factor matrices. This regression problem arises in each step of the widely-used alternating least squares (ALS) algorithm for computing the Tucker decomposition of a tensor. We present the first subquadratic-time algorithm for solving Kronecker regression to a $(1+\varepsilon)$-approximation that avoids the exponential term $O(\varepsilon^{-N})$ in the running time. Our techniques combine leverage score sampling and iterative methods. By extending our approach to block-design matrices where one block is a Kronecker product, we also achieve subquadratic-time algorithms for (1) Kronecker ridge regression and (2) updating the factor matrix of a Tucker decomposition in ALS, which is not a pure Kronecker regression problem, thereby improving the running time of all steps of Tucker ALS. We demonstrate the speed and accuracy of this Kronecker regression algorithm on synthetic data and real-world image tensors.

Fast Low-Rank Tensor Decomposition by Ridge Leverage Score Sampling

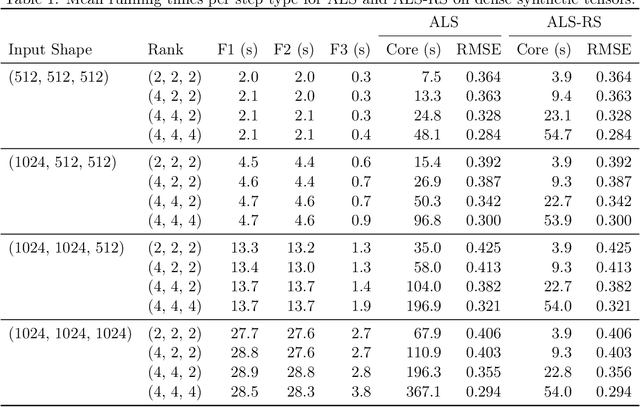
Low-rank tensor decomposition generalizes low-rank matrix approximation and is a powerful technique for discovering low-dimensional structure in high-dimensional data. In this paper, we study Tucker decompositions and use tools from randomized numerical linear algebra called ridge leverage scores to accelerate the core tensor update step in the widely-used alternating least squares (ALS) algorithm. Updating the core tensor, a severe bottleneck in ALS, is a highly-structured ridge regression problem where the design matrix is a Kronecker product of the factor matrices. We show how to use approximate ridge leverage scores to construct a sketched instance for any ridge regression problem such that the solution vector for the sketched problem is a $(1+\varepsilon)$-approximation to the original instance. Moreover, we show that classical leverage scores suffice as an approximation, which then allows us to exploit the Kronecker structure and update the core tensor in time that depends predominantly on the rank and the sketching parameters (i.e., sublinear in the size of the input tensor). We also give upper bounds for ridge leverage scores as rows are removed from the design matrix (e.g., if the tensor has missing entries), and we demonstrate the effectiveness of our approximate ridge regressioni algorithm for large, low-rank Tucker decompositions on both synthetic and real-world data.

Locality-Sensitive Hashing for f-Divergences: Mutual Information Loss and Beyond

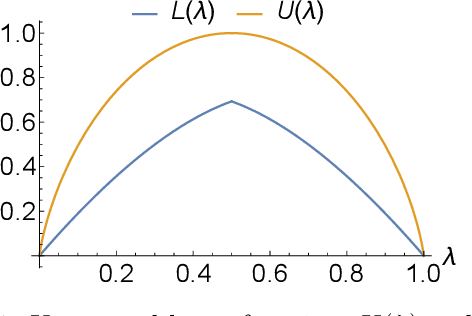
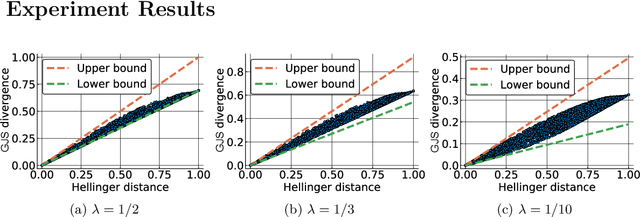
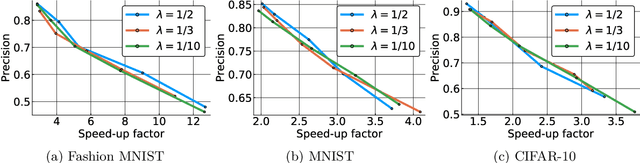
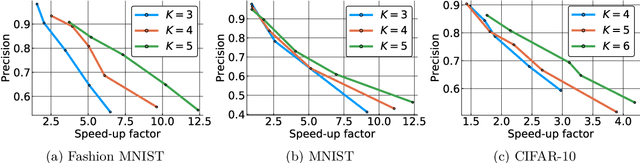
Computing approximate nearest neighbors in high dimensional spaces is a central problem in large-scale data mining with a wide range of applications in machine learning and data science. A popular and effective technique in computing nearest neighbors approximately is the locality-sensitive hashing (LSH) scheme. In this paper, we aim to develop LSH schemes for distance functions that measure the distance between two probability distributions, particularly for f-divergences as well as a generalization to capture mutual information loss. First, we provide a general framework to design LHS schemes for f-divergence distance functions and develop LSH schemes for the generalized Jensen-Shannon divergence and triangular discrimination in this framework. We show a two-sided approximation result for approximation of the generalized Jensen-Shannon divergence by the Hellinger distance, which may be of independent interest. Next, we show a general method of reducing the problem of designing an LSH scheme for a Krein kernel (which can be expressed as the difference of two positive definite kernels) to the problem of maximum inner product search. We exemplify this method by applying it to the mutual information loss, due to its several important applications such as model compression.

Categorical Feature Compression via Submodular Optimization

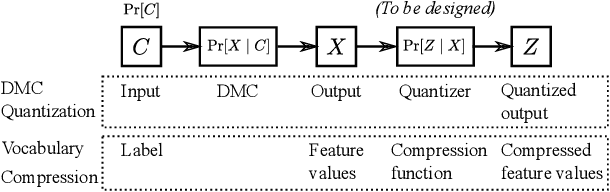
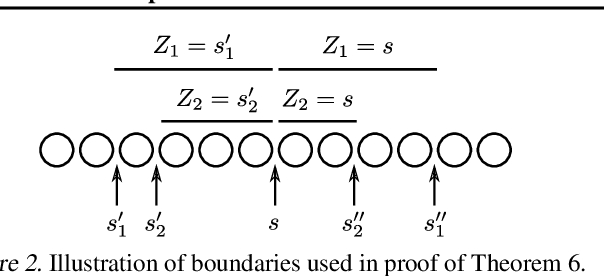
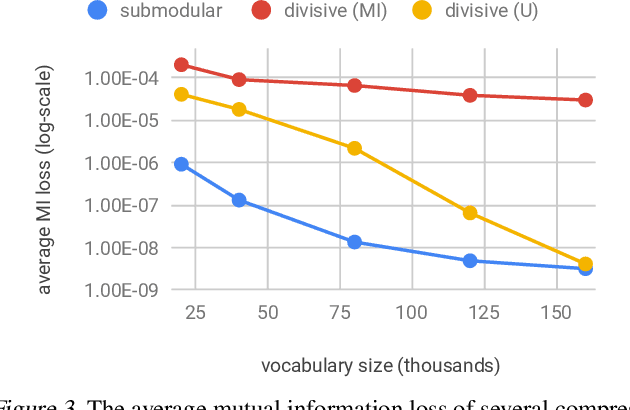
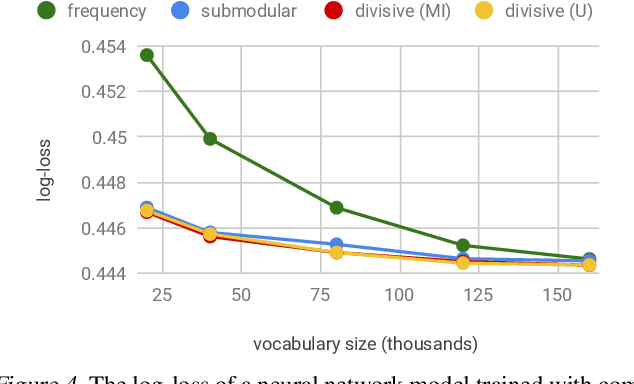
In the era of big data, learning from categorical features with very large vocabularies (e.g., 28 million for the Criteo click prediction dataset) has become a practical challenge for machine learning researchers and practitioners. We design a highly-scalable vocabulary compression algorithm that seeks to maximize the mutual information between the compressed categorical feature and the target binary labels and we furthermore show that its solution is guaranteed to be within a $1-1/e \approx 63\%$ factor of the global optimal solution. To achieve this, we introduce a novel re-parametrization of the mutual information objective, which we prove is submodular, and design a data structure to query the submodular function in amortized $O(\log n )$ time (where $n$ is the input vocabulary size). Our complete algorithm is shown to operate in $O(n \log n )$ time. Additionally, we design a distributed implementation in which the query data structure is decomposed across $O(k)$ machines such that each machine only requires $O(\frac n k)$ space, while still preserving the approximation guarantee and using only logarithmic rounds of computation. We also provide analysis of simple alternative heuristic compression methods to demonstrate they cannot achieve any approximation guarantee. Using the large-scale Criteo learning task, we demonstrate better performance in retaining mutual information and also verify competitive learning performance compared to other baseline methods.