Mehrdad Ghadiri
Fast Tensor Completion via Approximate Richardson Iteration
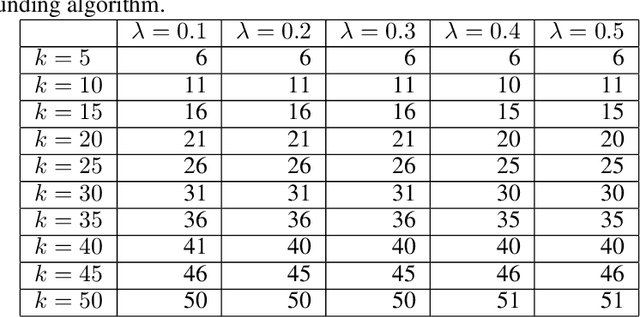
Feb 13, 2025Abstract:We study tensor completion (TC) through the lens of low-rank tensor decomposition (TD). Many TD algorithms use fast alternating minimization methods, which solve highly structured linear regression problems at each step (e.g., for CP, Tucker, and tensor-train decompositions). However, such algebraic structure is lost in TC regression problems, making direct extensions unclear. To address this, we propose a lifting approach that approximately solves TC regression problems using structured TD regression algorithms as blackbox subroutines, enabling sublinear-time methods. We theoretically analyze the convergence rate of our approximate Richardson iteration based algorithm, and we demonstrate on real-world tensors that its running time can be 100x faster than direct methods for CP completion.
Approximately Optimal Core Shapes for Tensor Decompositions
Feb 08, 2023Abstract:This work studies the combinatorial optimization problem of finding an optimal core tensor shape, also called multilinear rank, for a size-constrained Tucker decomposition. We give an algorithm with provable approximation guarantees for its reconstruction error via connections to higher-order singular values. Specifically, we introduce a novel Tucker packing problem, which we prove is NP-hard, and give a polynomial-time approximation scheme based on a reduction to the 2-dimensional knapsack problem with a matroid constraint. We also generalize our techniques to tree tensor network decompositions. We implement our algorithm using an integer programming solver, and show that its solution quality is competitive with (and sometimes better than) the greedy algorithm that uses the true Tucker decomposition loss at each step, while also running up to 1000x faster.
Subquadratic Kronecker Regression with Applications to Tensor Decomposition
Sep 11, 2022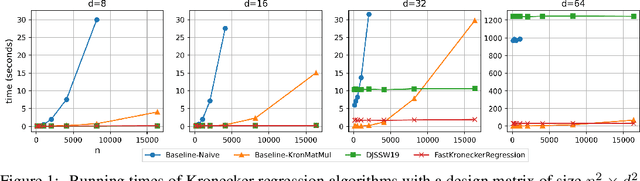
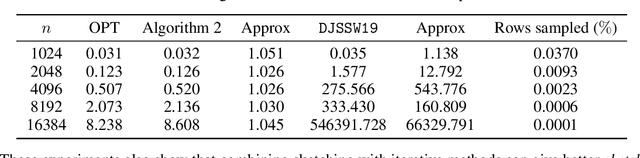
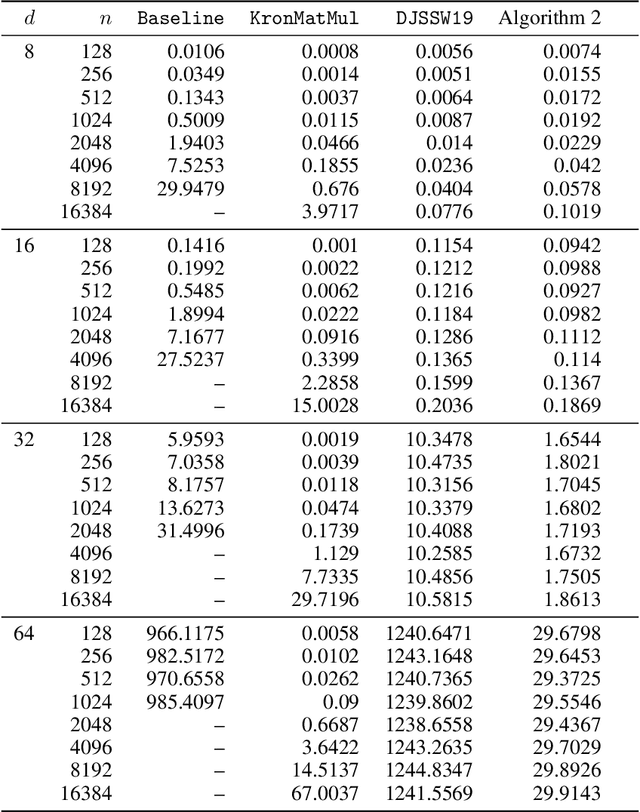
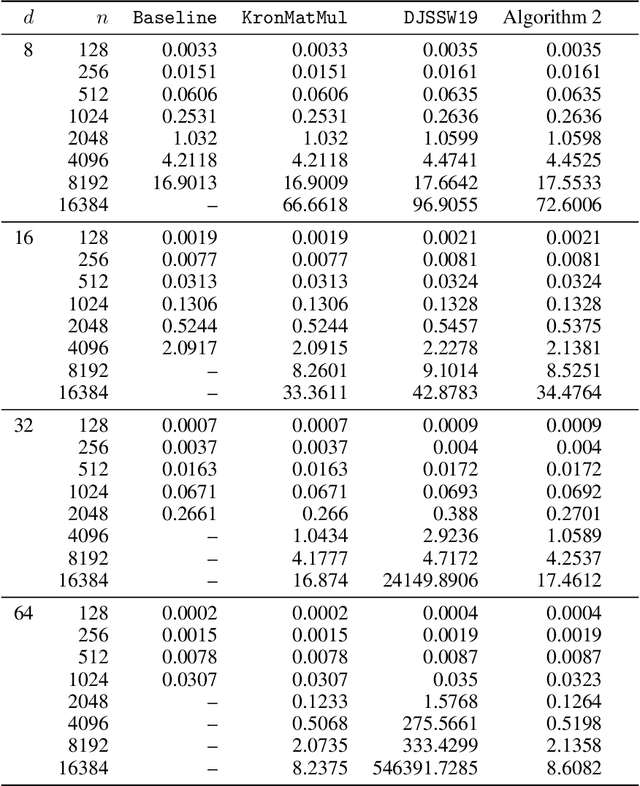
Abstract:Kronecker regression is a highly-structured least squares problem $\min_{\mathbf{x}} \lVert \mathbf{K}\mathbf{x} - \mathbf{b} \rVert_{2}^2$, where the design matrix $\mathbf{K} = \mathbf{A}^{(1)} \otimes \cdots \otimes \mathbf{A}^{(N)}$ is a Kronecker product of factor matrices. This regression problem arises in each step of the widely-used alternating least squares (ALS) algorithm for computing the Tucker decomposition of a tensor. We present the first subquadratic-time algorithm for solving Kronecker regression to a $(1+\varepsilon)$-approximation that avoids the exponential term $O(\varepsilon^{-N})$ in the running time. Our techniques combine leverage score sampling and iterative methods. By extending our approach to block-design matrices where one block is a Kronecker product, we also achieve subquadratic-time algorithms for (1) Kronecker ridge regression and (2) updating the factor matrix of a Tucker decomposition in ALS, which is not a pure Kronecker regression problem, thereby improving the running time of all steps of Tucker ALS. We demonstrate the speed and accuracy of this Kronecker regression algorithm on synthetic data and real-world image tensors.
Constant-Factor Approximation Algorithms for Socially Fair $k$-Clustering
Jun 22, 2022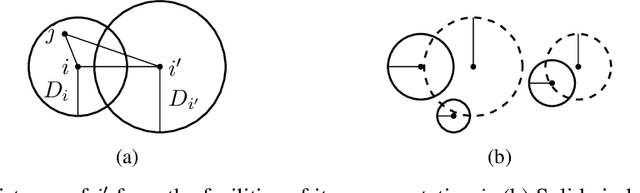
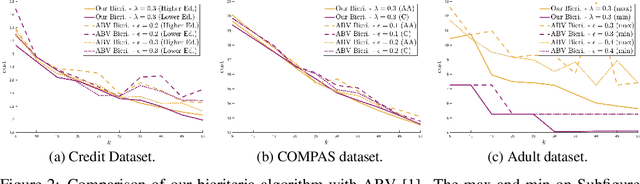

Abstract:We study approximation algorithms for the socially fair $(\ell_p, k)$-clustering problem with $m$ groups, whose special cases include the socially fair $k$-median ($p=1$) and socially fair $k$-means ($p=2$) problems. We present (1) a polynomial-time $(5+2\sqrt{6})^p$-approximation with at most $k+m$ centers (2) a $(5+2\sqrt{6}+\epsilon)^p$-approximation with $k$ centers in time $n^{2^{O(p)}\cdot m^2}$, and (3) a $(15+6\sqrt{6})^p$ approximation with $k$ centers in time $k^{m}\cdot\text{poly}(n)$. The first result is obtained via a refinement of the iterative rounding method using a sequence of linear programs. The latter two results are obtained by converting a solution with up to $k+m$ centers to one with $k$ centers using sparsification methods for (2) and via an exhaustive search for (3). We also compare the performance of our algorithms with existing bicriteria algorithms as well as exactly $k$ center approximation algorithms on benchmark datasets, and find that our algorithms also outperform existing methods in practice.
Fast Low-Rank Tensor Decomposition by Ridge Leverage Score Sampling
Jul 22, 2021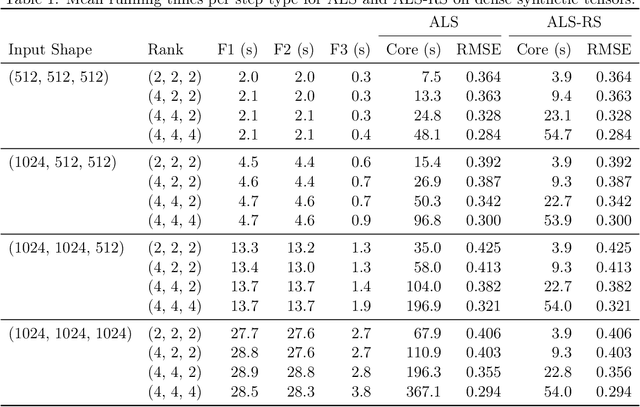
Abstract:Low-rank tensor decomposition generalizes low-rank matrix approximation and is a powerful technique for discovering low-dimensional structure in high-dimensional data. In this paper, we study Tucker decompositions and use tools from randomized numerical linear algebra called ridge leverage scores to accelerate the core tensor update step in the widely-used alternating least squares (ALS) algorithm. Updating the core tensor, a severe bottleneck in ALS, is a highly-structured ridge regression problem where the design matrix is a Kronecker product of the factor matrices. We show how to use approximate ridge leverage scores to construct a sketched instance for any ridge regression problem such that the solution vector for the sketched problem is a $(1+\varepsilon)$-approximation to the original instance. Moreover, we show that classical leverage scores suffice as an approximation, which then allows us to exploit the Kronecker structure and update the core tensor in time that depends predominantly on the rank and the sketching parameters (i.e., sublinear in the size of the input tensor). We also give upper bounds for ridge leverage scores as rows are removed from the design matrix (e.g., if the tensor has missing entries), and we demonstrate the effectiveness of our approximate ridge regressioni algorithm for large, low-rank Tucker decompositions on both synthetic and real-world data.
A Parameterized Family of Meta-Submodular Functions
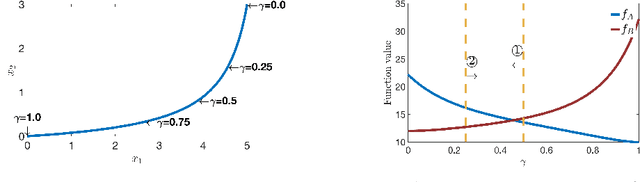
Jun 23, 2020Abstract:Submodular function maximization has found a wealth of new applications in machine learning models during the past years. The related supermodular maximization models (submodular minimization) also offer an abundance of applications, but they appeared to be highly intractable even under simple cardinality constraints. Hence, while there are well-developed tools for maximizing a submodular function subject to a matroid constraint, there is much less work on the corresponding supermodular maximization problems. We give a broad parameterized family of monotone functions which includes submodular functions and a class of supermodular functions containing diversity functions. Functions in this parameterized family are called \emph{$\gamma$-meta-submodular}. We develop local search algorithms with approximation factors that depend only on the parameter $\gamma$. We show that the $\gamma$-meta-submodular families include well-known classes of functions such as meta-submodular functions ($\gamma=0$), metric diversity functions and proportionally submodular functions (both with $\gamma=1$), diversity functions based on negative-type distances or Jensen-Shannon divergence (both with $\gamma=2$), and $\sigma$-semi metric diversity functions ($\gamma = \sigma$).
Fair k-Means Clustering
Jun 17, 2020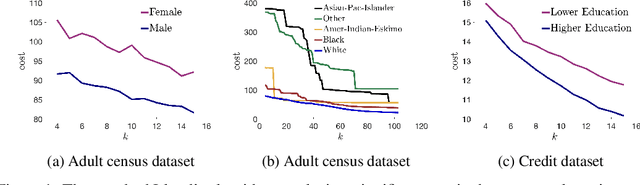
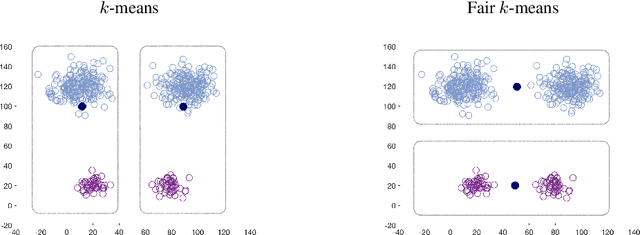
Abstract:We show that the popular $k$-means clustering algorithm (Lloyd's heuristic), used for a variety of scientific data, can result in outcomes that are unfavorable to subgroups of data (e.g., demographic groups). Such biased clusterings can have deleterious implications for human-centric applications such as resource allocation. We present a fair $k$-means objective and algorithm to choose cluster centers that provide equitable costs for different groups. The algorithm, Fair-Lloyd, is a modification of Lloyd's heuristic for $k$-means, inheriting its simplicity, efficiency, and stability. In comparison with standard Lloyd's, we find that on benchmark data sets, Fair-Lloyd exhibits unbiased performance by ensuring that all groups have balanced costs in the output $k$-clustering, while incurring a negligible increase in running time, thus making it a viable fair option wherever $k$-means is currently used.
Amortized Rejection Sampling in Universal Probabilistic Programming
Nov 30, 2019
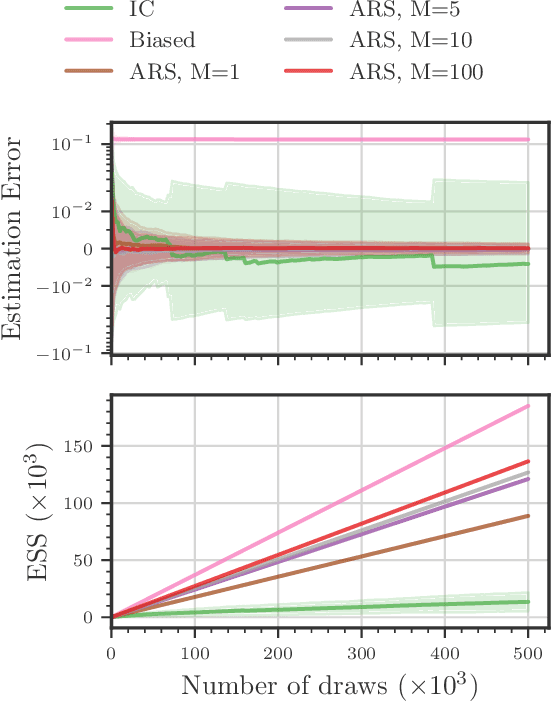
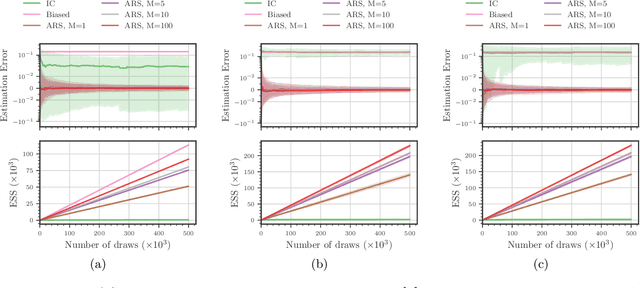
Abstract:Existing approaches to amortized inference in probabilistic programs with unbounded loops can produce estimators with infinite variance. An instance of this is importance sampling inference in programs that explicitly include rejection sampling as part of the user-programmed generative procedure. In this paper we develop a new and efficient amortized importance sampling estimator. We prove finite variance of our estimator and empirically demonstrate our method's correctness and efficiency compared to existing alternatives on generative programs containing rejection sampling loops and discuss how to implement our method in a generic probabilistic programming framework.
Distributed Maximization of "Submodular plus Diversity" Functions for Multi-label Feature Selection on Huge Datasets
Mar 20, 2019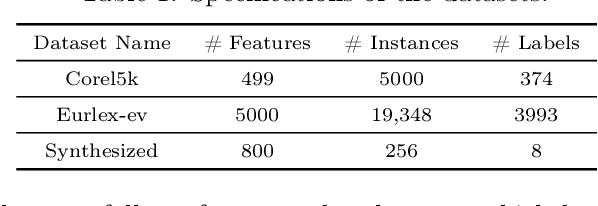
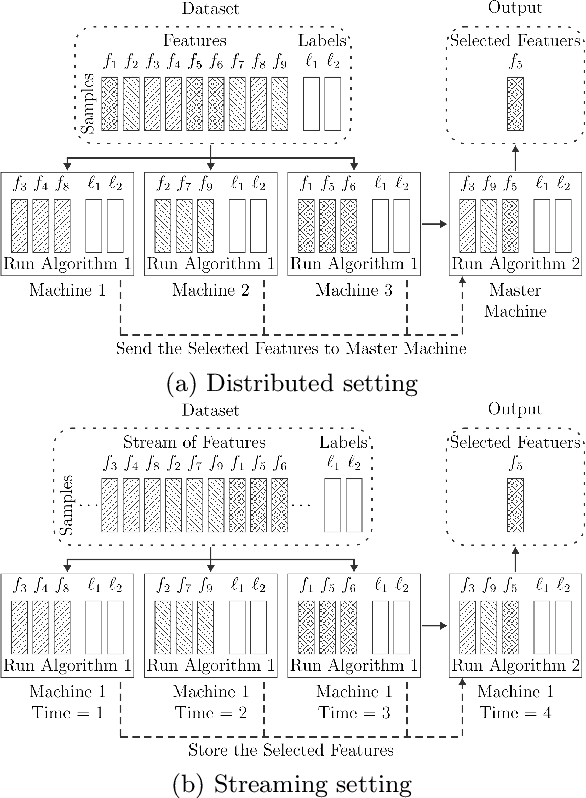
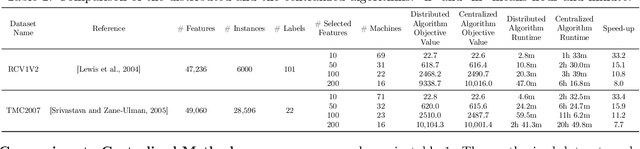
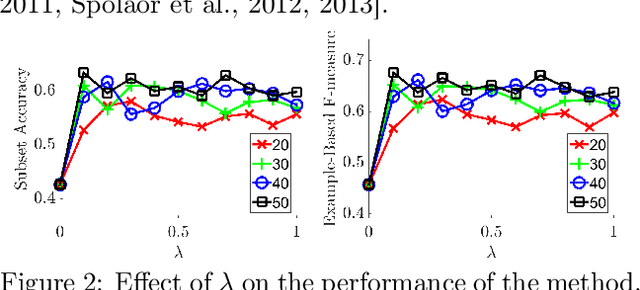
Abstract:There are many problems in machine learning and data mining which are equivalent to selecting a non-redundant, high "quality" set of objects. Recommender systems, feature selection, and data summarization are among many applications of this. In this paper, we consider this problem as an optimization problem that seeks to maximize the sum of a sum-sum diversity function and a non-negative monotone submodular function. The diversity function addresses the redundancy, and the submodular function controls the predictive quality. We consider the problem in big data settings (in other words, distributed and streaming settings) where the data cannot be stored on a single machine or the process time is too high for a single machine. We show that a greedy algorithm achieves a constant factor approximation of the optimal solution in these settings. Moreover, we formulate the multi-label feature selection problem as such an optimization problem. This formulation combined with our algorithm leads to the first distributed multi-label feature selection method. We compare the performance of this method with centralized multi-label feature selection methods in the literature, and we show that its performance is comparable or in some cases is even better than current centralized multi-label feature selection methods.
Active Distance-Based Clustering using K-medoids
Dec 12, 2015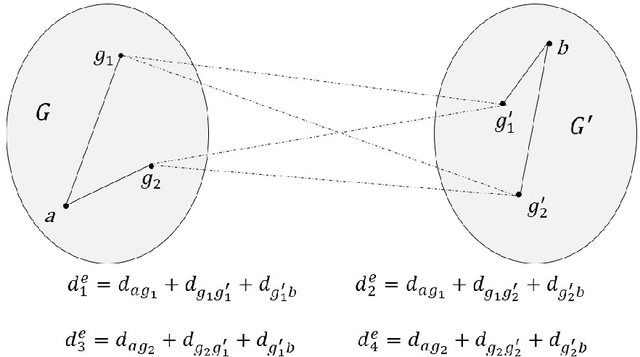
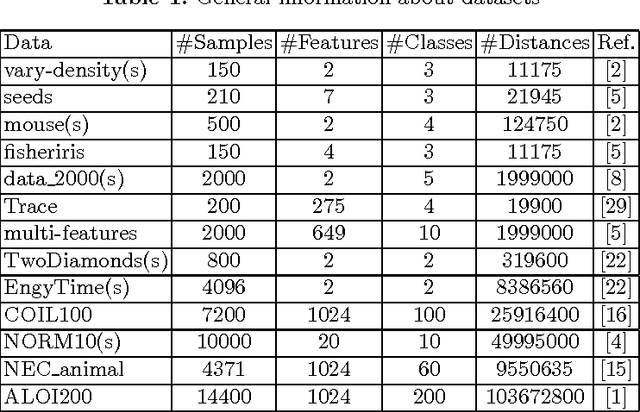
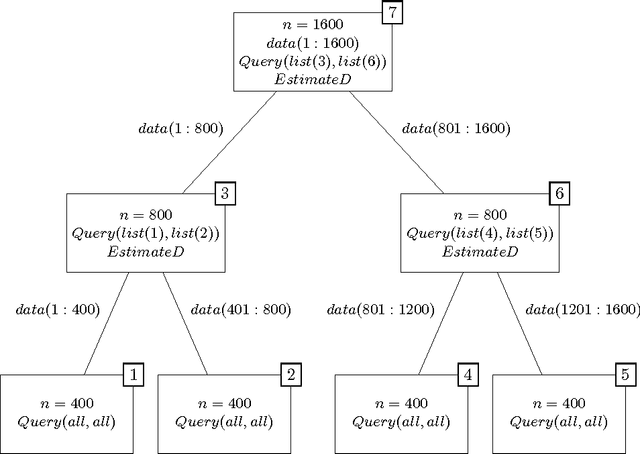
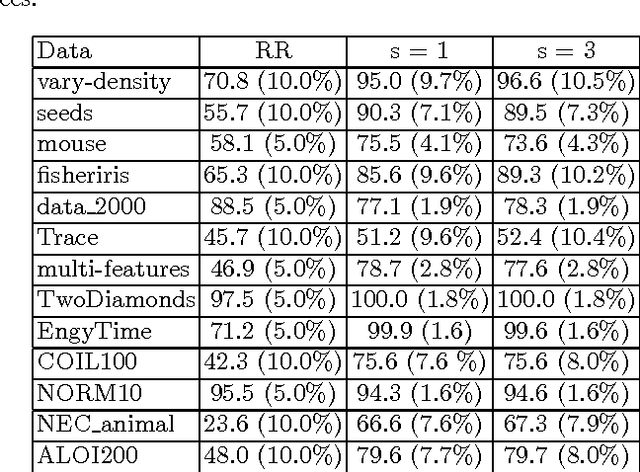
Abstract:k-medoids algorithm is a partitional, centroid-based clustering algorithm which uses pairwise distances of data points and tries to directly decompose the dataset with $n$ points into a set of $k$ disjoint clusters. However, k-medoids itself requires all distances between data points that are not so easy to get in many applications. In this paper, we introduce a new method which requires only a small proportion of the whole set of distances and makes an effort to estimate an upper-bound for unknown distances using the inquired ones. This algorithm makes use of the triangle inequality to calculate an upper-bound estimation of the unknown distances. Our method is built upon a recursive approach to cluster objects and to choose some points actively from each bunch of data and acquire the distances between these prominent points from oracle. Experimental results show that the proposed method using only a small subset of the distances can find proper clustering on many real-world and synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge