TorchDriveEnv: A Reinforcement Learning Benchmark for Autonomous Driving with Reactive, Realistic, and Diverse Non-Playable Characters

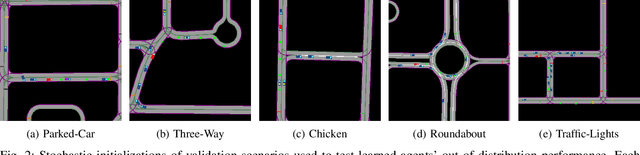
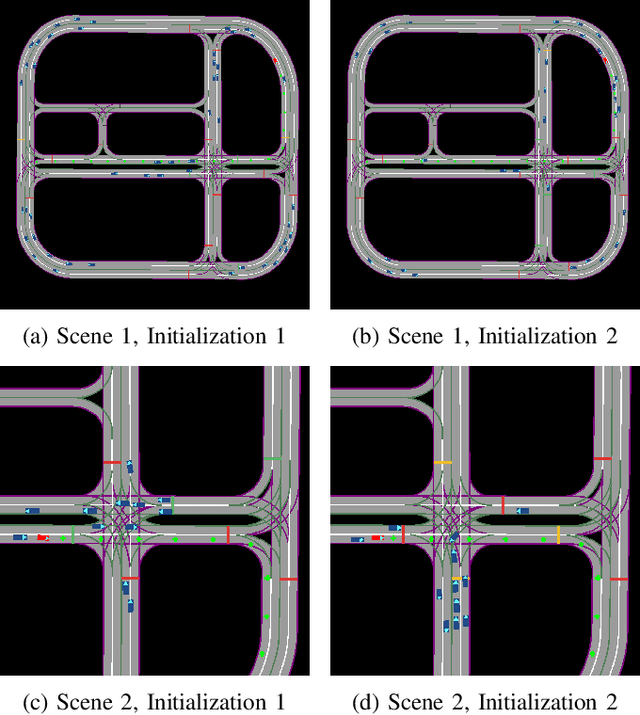
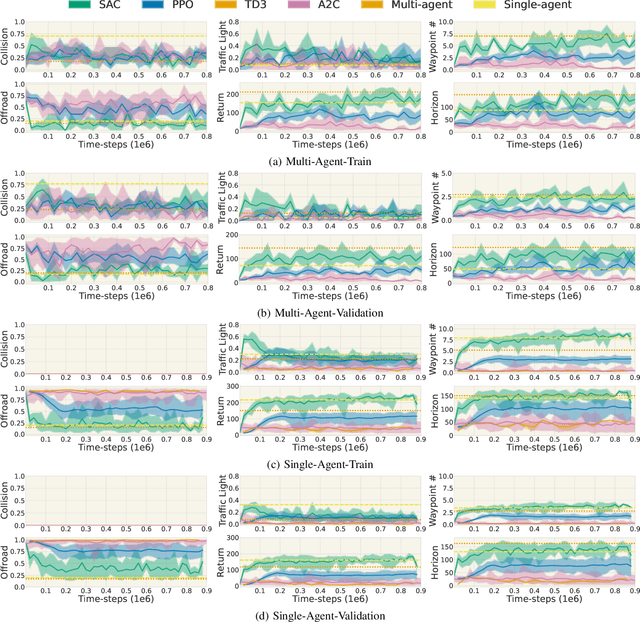
The training, testing, and deployment, of autonomous vehicles requires realistic and efficient simulators. Moreover, because of the high variability between different problems presented in different autonomous systems, these simulators need to be easy to use, and easy to modify. To address these problems we introduce TorchDriveSim and its benchmark extension TorchDriveEnv. TorchDriveEnv is a lightweight reinforcement learning benchmark programmed entirely in Python, which can be modified to test a number of different factors in learned vehicle behavior, including the effect of varying kinematic models, agent types, and traffic control patterns. Most importantly unlike many replay based simulation approaches, TorchDriveEnv is fully integrated with a state of the art behavioral simulation API. This allows users to train and evaluate driving models alongside data driven Non-Playable Characters (NPC) whose initializations and driving behavior are reactive, realistic, and diverse. We illustrate the efficiency and simplicity of TorchDriveEnv by evaluating common reinforcement learning baselines in both training and validation environments. Our experiments show that TorchDriveEnv is easy to use, but difficult to solve.

Nearest Neighbour Score Estimators for Diffusion Generative Models

Score function estimation is the cornerstone of both training and sampling from diffusion generative models. Despite this fact, the most commonly used estimators are either biased neural network approximations or high variance Monte Carlo estimators based on the conditional score. We introduce a novel nearest neighbour score function estimator which utilizes multiple samples from the training set to dramatically decrease estimator variance. We leverage our low variance estimator in two compelling applications. Training consistency models with our estimator, we report a significant increase in both convergence speed and sample quality. In diffusion models, we show that our estimator can replace a learned network for probability-flow ODE integration, opening promising new avenues of future research.

Video Killed the HD-Map: Predicting Driving Behavior Directly From Drone Images

The development of algorithms that learn behavioral driving models using human demonstrations has led to increasingly realistic simulations. In general, such models learn to jointly predict trajectories for all controlled agents by exploiting road context information such as drivable lanes obtained from manually annotated high-definition (HD) maps. Recent studies show that these models can greatly benefit from increasing the amount of human data available for training. However, the manual annotation of HD maps which is necessary for every new location puts a bottleneck on efficiently scaling up human traffic datasets. We propose a drone birdview image-based map (DBM) representation that requires minimal annotation and provides rich road context information. We evaluate multi-agent trajectory prediction using the DBM by incorporating it into a differentiable driving simulator as an image-texture-based differentiable rendering module. Our results demonstrate competitive multi-agent trajectory prediction performance when using our DBM representation as compared to models trained with rasterized HD maps.

Conditional Permutation Invariant Flows

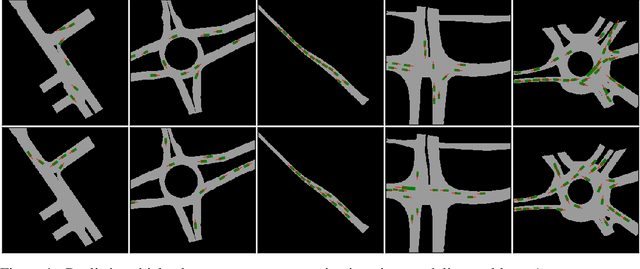
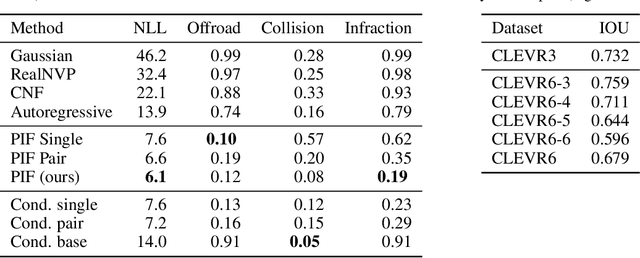
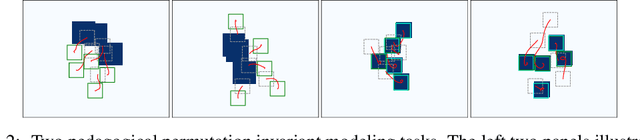
We present a novel, conditional generative probabilistic model of set-valued data with a tractable log density. This model is a continuous normalizing flow governed by permutation equivariant dynamics. These dynamics are driven by a learnable per-set-element term and pairwise interactions, both parametrized by deep neural networks. We illustrate the utility of this model via applications including (1) complex traffic scene generation conditioned on visually specified map information, and (2) object bounding box generation conditioned directly on images. We train our model by maximizing the expected likelihood of labeled conditional data under our flow, with the aid of a penalty that ensures the dynamics are smooth and hence efficiently solvable. Our method significantly outperforms non-permutation invariant baselines in terms of log likelihood and domain-specific metrics (offroad, collision, and combined infractions), yielding realistic samples that are difficult to distinguish from real data.

Differentiable Particle Filtering without Modifying the Forward Pass

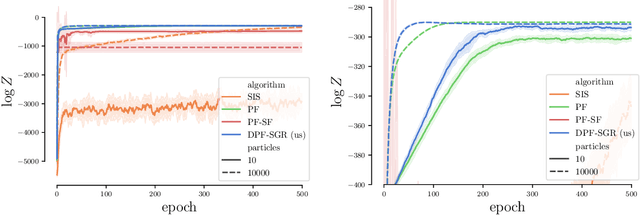
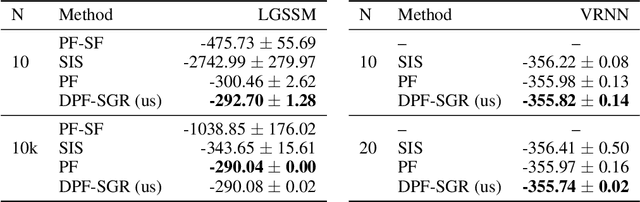
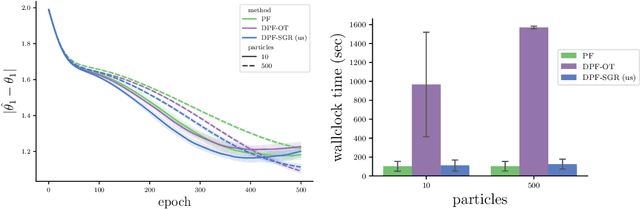
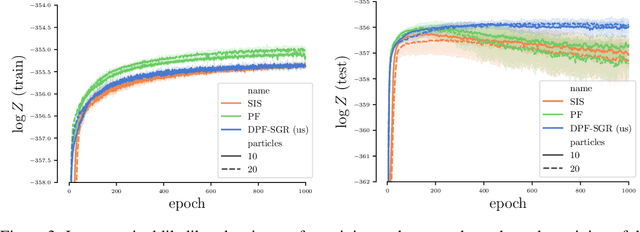
In recent years particle filters have being used as components in systems optimized end-to-end with gradient descent. However, the resampling step in a particle filter is not differentiable, which biases gradients and interferes with optimization. To remedy this problem, several differentiable variants of resampling have been proposed, all of which modify the behavior of the particle filter in significant and potentially undesirable ways. In this paper, we show how to obtain unbiased estimators of the gradient of the marginal likelihood by only modifying messages used in backpropagation, leaving the standard forward pass of a particle filter unchanged. Our method is simple to implement, has a low computational overhead, does not introduce additional hyperparameters, and extends to derivatives of higher orders. We call it stop-gradient resampling, since it can easily be implemented with automatic differentiation libraries using the stop-gradient operator instead of explicitly modifying the backward messages.

Amortized Rejection Sampling in Universal Probabilistic Programming

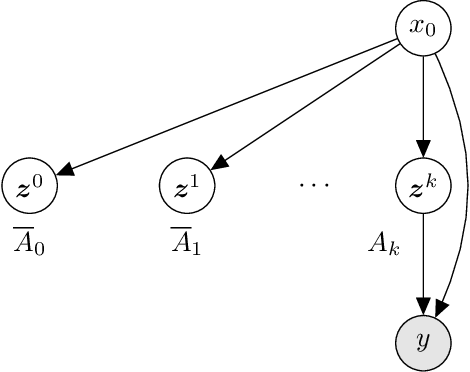
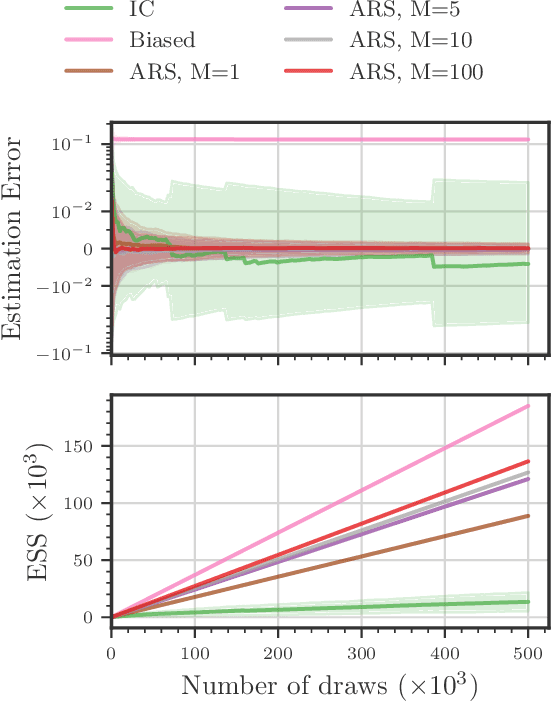
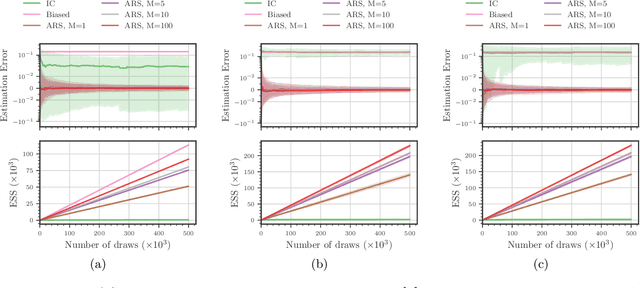
Existing approaches to amortized inference in probabilistic programs with unbounded loops can produce estimators with infinite variance. An instance of this is importance sampling inference in programs that explicitly include rejection sampling as part of the user-programmed generative procedure. In this paper we develop a new and efficient amortized importance sampling estimator. We prove finite variance of our estimator and empirically demonstrate our method's correctness and efficiency compared to existing alternatives on generative programs containing rejection sampling loops and discuss how to implement our method in a generic probabilistic programming framework.

Deep Probabilistic Surrogate Networks for Universal Simulator Approximation

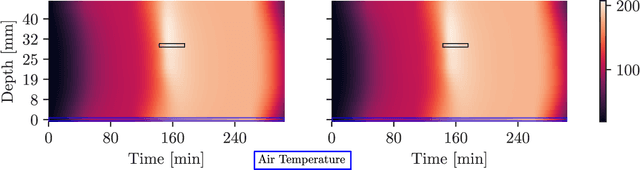
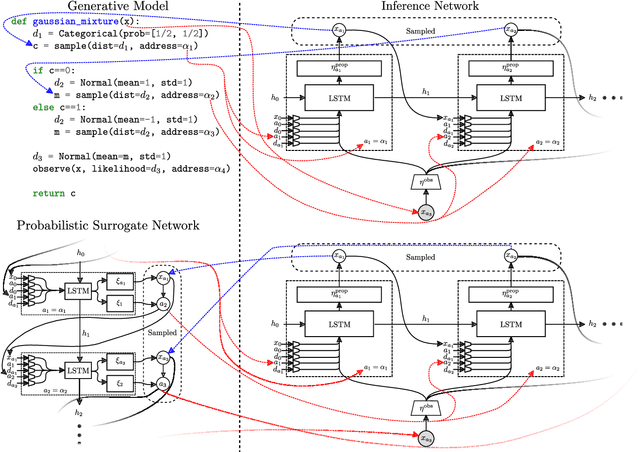
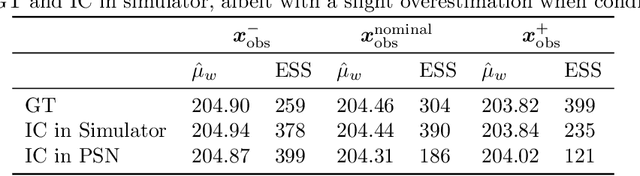
We present a framework for automatically structuring and training fast, approximate, deep neural surrogates of existing stochastic simulators. Unlike traditional approaches to surrogate modeling, our surrogates retain the interpretable structure of the reference simulators. The particular way we achieve this allows us to replace the reference simulator with the surrogate when undertaking amortized inference in the probabilistic programming sense. The fidelity and speed of our surrogates allow for not only faster "forward" stochastic simulation but also for accurate and substantially faster inference. We support these claims via experiments that involve a commercial composite-materials curing simulator. Employing our surrogate modeling technique makes inference an order of magnitude faster, opening up the possibility of doing simulator-based, non-invasive, just-in-time parts quality testing; in this case inferring safety-critical latent internal temperature profiles of composite materials undergoing curing from surface temperature profile measurements.

Composing Modeling and Inference Operations with Probabilistic Program Combinators

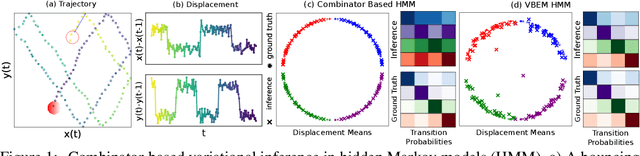
Probabilistic programs with dynamic computation graphs can define measures over sample spaces with unbounded dimensionality, which constitute programmatic analogues to Bayesian nonparametrics. Owing to the generality of this model class, inference relies on `black-box' Monte Carlo methods that are often not able to take advantage of conditional independence and exchangeability, which have historically been the cornerstones of efficient inference. We here seek to develop a `middle ground' between probabilistic models with fully dynamic and fully static computation graphs. To this end, we introduce a combinator library for the Probabilistic Torch framework. Combinators are functions that accept models and return transformed models. We assume that models are dynamic, but that model composition is static, in the sense that combinator application takes place prior to evaluating the model on data. Combinators provide primitives for both model and inference composition. Model combinators take the form of classic functional programming constructs such as map and reduce. These constructs define a computation graph at a coarsened level of representation, in which nodes correspond to models, rather than individual variables. Inference combinators implement operations such as importance resampling and application of a transition kernel, which alter the evaluation strategy for a model whilst preserving proper weighting. Owing to this property, models defined using combinators can be trained using stochastic methods that optimize either variational or wake-sleep style objectives. As a validation of this principle, we use combinators to implement black box inference for hidden Markov models.

Consistent Kernel Mean Estimation for Functions of Random Variables

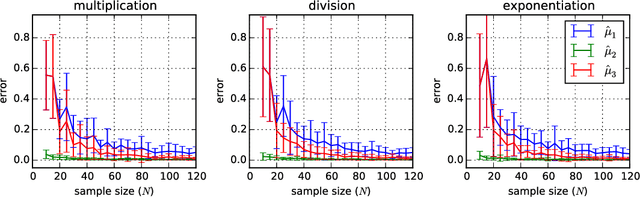
We provide a theoretical foundation for non-parametric estimation of functions of random variables using kernel mean embeddings. We show that for any continuous function $f$, consistent estimators of the mean embedding of a random variable $X$ lead to consistent estimators of the mean embedding of $f(X)$. For Mat\'ern kernels and sufficiently smooth functions we also provide rates of convergence. Our results extend to functions of multiple random variables. If the variables are dependent, we require an estimator of the mean embedding of their joint distribution as a starting point; if they are independent, it is sufficient to have separate estimators of the mean embeddings of their marginal distributions. In either case, our results cover both mean embeddings based on i.i.d. samples as well as "reduced set" expansions in terms of dependent expansion points. The latter serves as a justification for using such expansions to limit memory resources when applying the approach as a basis for probabilistic programming.