Consistent Kernel Mean Estimation for Functions of Random Variables
Paper and Code
Oct 19, 2016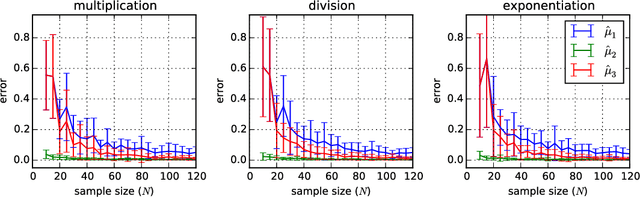
We provide a theoretical foundation for non-parametric estimation of functions of random variables using kernel mean embeddings. We show that for any continuous function $f$, consistent estimators of the mean embedding of a random variable $X$ lead to consistent estimators of the mean embedding of $f(X)$. For Mat\'ern kernels and sufficiently smooth functions we also provide rates of convergence. Our results extend to functions of multiple random variables. If the variables are dependent, we require an estimator of the mean embedding of their joint distribution as a starting point; if they are independent, it is sufficient to have separate estimators of the mean embeddings of their marginal distributions. In either case, our results cover both mean embeddings based on i.i.d. samples as well as "reduced set" expansions in terms of dependent expansion points. The latter serves as a justification for using such expansions to limit memory resources when applying the approach as a basis for probabilistic programming.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge