A Hitchhiker's Guide to Poisson Gradient Estimation

Poisson-distributed latent variable models are widely used in computational neuroscience, but differentiating through discrete stochastic samples remains challenging. Two approaches address this: Exponential Arrival Time (EAT) simulation and Gumbel-SoftMax (GSM) relaxation. We provide the first systematic comparison of these methods, along with practical guidance for practitioners. Our main technical contribution is a modification to the EAT method that theoretically guarantees an unbiased first moment (exactly matching the firing rate), and reduces second-moment bias. We evaluate these methods on their distributional fidelity, gradient quality, and performance on two tasks: (1) variational autoencoders with Poisson latents, and (2) partially observable generalized linear models, where latent neural connectivity must be inferred from observed spike trains. Across all metrics, our modified EAT method exhibits better overall performance (often comparable to exact gradients), and substantially higher robustness to hyperparameter choices. Together, our results clarify the trade-offs between these methods and offer concrete recommendations for practitioners working with Poisson latent variable models.

Divide-and-Conquer Predictive Coding: a structured Bayesian inference algorithm

Unexpected stimuli induce "error" or "surprise" signals in the brain. The theory of predictive coding promises to explain these observations in terms of Bayesian inference by suggesting that the cortex implements variational inference in a probabilistic graphical model. However, when applied to machine learning tasks, this family of algorithms has yet to perform on par with other variational approaches in high-dimensional, structured inference problems. To address this, we introduce a novel predictive coding algorithm for structured generative models, that we call divide-and-conquer predictive coding (DCPC). DCPC differs from other formulations of predictive coding, as it respects the correlation structure of the generative model and provably performs maximum-likelihood updates of model parameters, all without sacrificing biological plausibility. Empirically, DCPC achieves better numerical performance than competing algorithms and provides accurate inference in a number of problems not previously addressed with predictive coding. We provide an open implementation of DCPC in Pyro on Github.

String Diagrams with Factorized Densities

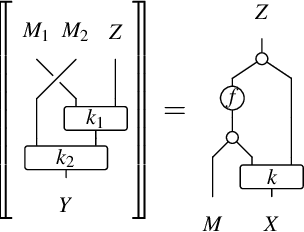
A growing body of research on probabilistic programs and causal models has highlighted the need to reason compositionally about model classes that extend directed graphical models. Both probabilistic programs and causal models define a joint probability density over a set of random variables, and exhibit sparse structure that can be used to reason about causation and conditional independence. This work builds on recent work on Markov categories of probabilistic mappings to define a category whose morphisms combine a joint density, factorized over each sample space, with a deterministic mapping from samples to return values. This is a step towards closing the gap between recent category-theoretic descriptions of probability measures, and the operational definitions of factorized densities that are commonly employed in probabilistic programming and causal inference.

Computing with Categories in Machine Learning

Category theory has been successfully applied in various domains of science, shedding light on universal principles unifying diverse phenomena and thereby enabling knowledge transfer between them. Applications to machine learning have been pursued recently, and yet there is still a gap between abstract mathematical foundations and concrete applications to machine learning tasks. In this paper we introduce DisCoPyro as a categorical structure learning framework, which combines categorical structures (such as symmetric monoidal categories and operads) with amortized variational inference, and can be applied, e.g., in program learning for variational autoencoders. We provide both mathematical foundations and concrete applications together with comparison of experimental performance with other models (e.g., neuro-symbolic models). We speculate that DisCoPyro could ultimately contribute to the development of artificial general intelligence.

Deriving time-averaged active inference from control principles

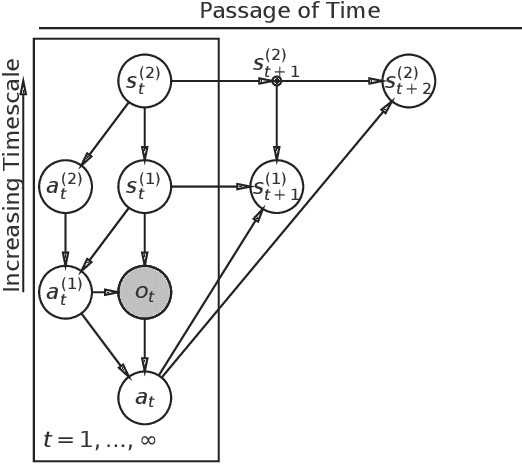
Active inference offers a principled account of behavior as minimizing average sensory surprise over time. Applications of active inference to control problems have heretofore tended to focus on finite-horizon or discounted-surprise problems, despite deriving from the infinite-horizon, average-surprise imperative of the free-energy principle. Here we derive an infinite-horizon, average-surprise formulation of active inference from optimal control principles. Our formulation returns to the roots of active inference in neuroanatomy and neurophysiology, formally reconnecting active inference to optimal feedback control. Our formulation provides a unified objective functional for sensorimotor control and allows for reference states to vary over time.

A Probabilistic Generative Model of Free Categories

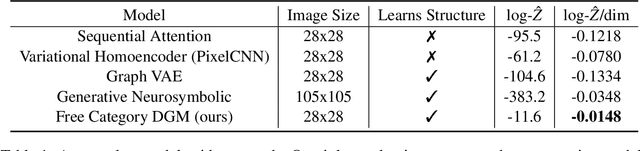
Applied category theory has recently developed libraries for computing with morphisms in interesting categories, while machine learning has developed ways of learning programs in interesting languages. Taking the analogy between categories and languages seriously, this paper defines a probabilistic generative model of morphisms in free monoidal categories over domain-specific generating objects and morphisms. The paper shows how acyclic directed wiring diagrams can model specifications for morphisms, which the model can use to generate morphisms. Amortized variational inference in the generative model then enables learning of parameters (by maximum likelihood) and inference of latent variables (by Bayesian inversion). A concrete experiment shows that the free category prior achieves competitive reconstruction performance on the Omniglot dataset.

Learning Proposals for Probabilistic Programs with Inference Combinators

We develop operators for construction of proposals in probabilistic programs, which we refer to as inference combinators. Inference combinators define a grammar over importance samplers that compose primitive operations such as application of a transition kernel and importance resampling. Proposals in these samplers can be parameterized using neural networks, which in turn can be trained by optimizing variational objectives. The result is a framework for user-programmable variational methods that are correct by construction and can be tailored to specific models. We demonstrate the flexibility of this framework by implementing advanced variational methods based on amortized Gibbs sampling and annealing.

Learning a Deep Generative Model like a Program: the Free Category Prior

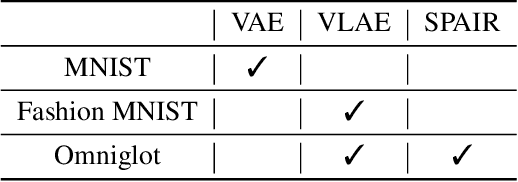
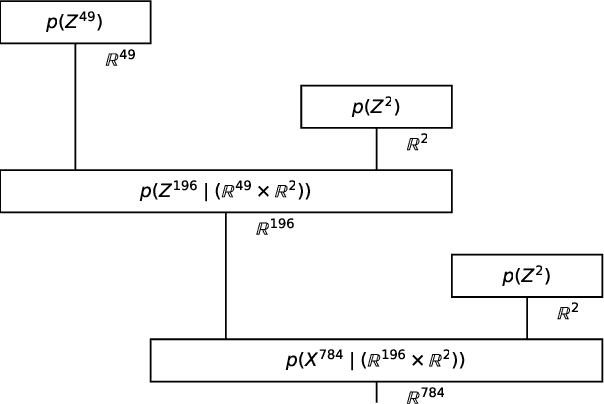
Humans surpass the cognitive abilities of most other animals in our ability to "chunk" concepts into words, and then combine the words to combine the concepts. In this process, we make "infinite use of finite means", enabling us to learn new concepts quickly and nest concepts within each-other. While program induction and synthesis remain at the heart of foundational theories of artificial intelligence, only recently has the community moved forward in attempting to use program learning as a benchmark task itself. The cognitive science community has thus often assumed that if the brain has simulation and reasoning capabilities equivalent to a universal computer, then it must employ a serialized, symbolic representation. Here we confront that assumption, and provide a counterexample in which compositionality is expressed via network structure: the free category prior over programs. We show how our formalism allows neural networks to serve as primitives in probabilistic programs. We learn both program structure and model parameters end-to-end.

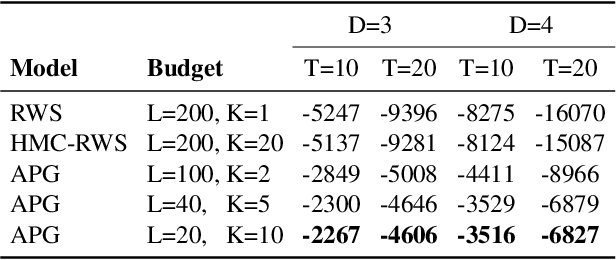
Amortized Population Gibbs Samplers with Neural Sufficient Statistics

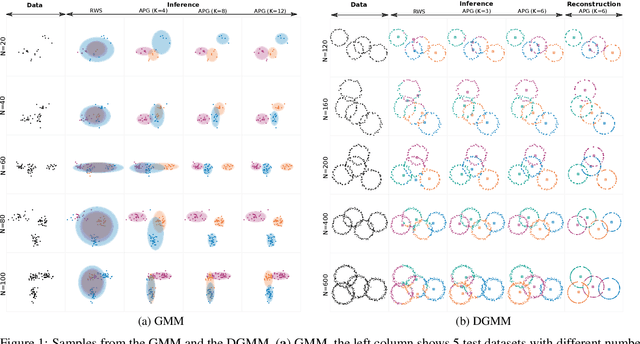
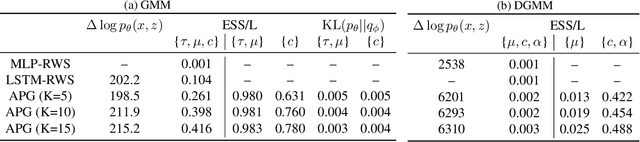
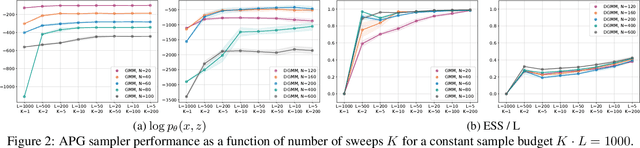
We develop amortized population Gibbs (APG) samplers, a new class of autoencoding variational methods for deep probabilistic models. APG samplers construct high-dimensional proposals by iterating over updates to lower-dimensional blocks of variables. Each conditional update is a neural proposal, which we train by minimizing the inclusive KL divergence relative to the conditional posterior. To appropriately account for the size of the input data, we develop a new parameterization in terms of neural sufficient statistics, resulting in quasi-conjugate variational approximations. Experiments demonstrate that learned proposals converge to the known analytical conditional posterior in conjugate models, and that APG samplers can learn inference networks for highly-structured deep generative models when the conditional posteriors are intractable. Here APG samplers offer a path toward scaling up stochastic variational methods to models in which standard autoencoding architectures fail to produce accurate samples.

Neural Topographic Factor Analysis for fMRI Data

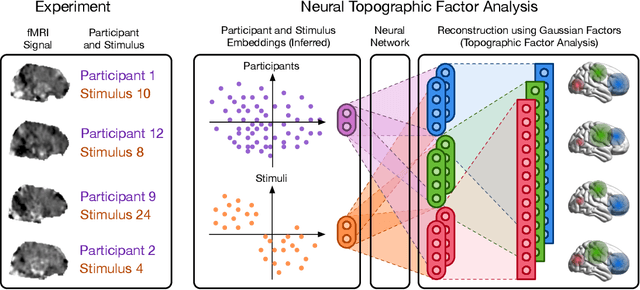
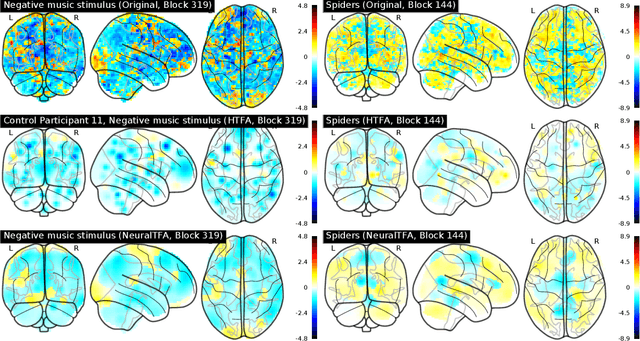
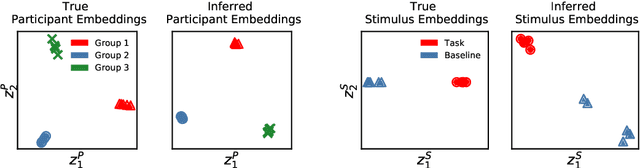
Neuroimaging experiments produce a large volume (gigabytes) of high-dimensional spatio-temporal data for a small number of sampled participants and stimuli. Analyses of this data commonly compute averages over all trials, ignoring variation within groups of participants and stimuli. To enable the analysis of fMRI data without this implicit assumption of uniformity, we propose Neural Topographic Factor Analysis (NTFA), a deep generative model that parameterizes factors as functions of embeddings for participants and stimuli. We evaluate NTFA on a synthetically generated dataset as well as on three datasets from fMRI experiments. Our results demonstrate that NTFA yields more accurate reconstructions than a state-of-the-art method with fewer parameters. Moreover, learned embeddings uncover latent categories of participants and stimuli, which suggests that NTFA takes a first step towards reasoning about individual variation in fMRI experiments.