Deriving time-averaged active inference from control principles
Paper and Code
Aug 22, 2022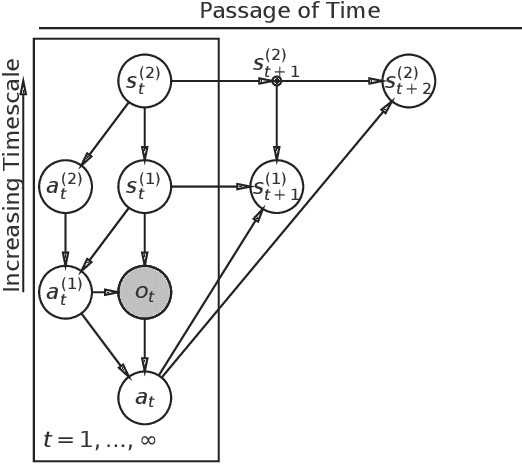

Active inference offers a principled account of behavior as minimizing average sensory surprise over time. Applications of active inference to control problems have heretofore tended to focus on finite-horizon or discounted-surprise problems, despite deriving from the infinite-horizon, average-surprise imperative of the free-energy principle. Here we derive an infinite-horizon, average-surprise formulation of active inference from optimal control principles. Our formulation returns to the roots of active inference in neuroanatomy and neurophysiology, formally reconnecting active inference to optimal feedback control. Our formulation provides a unified objective functional for sensorimotor control and allows for reference states to vary over time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge