String Diagrams with Factorized Densities
Paper and Code
May 04, 2023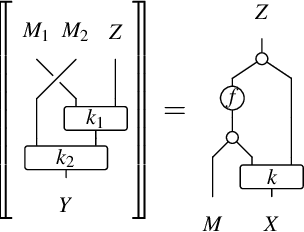
A growing body of research on probabilistic programs and causal models has highlighted the need to reason compositionally about model classes that extend directed graphical models. Both probabilistic programs and causal models define a joint probability density over a set of random variables, and exhibit sparse structure that can be used to reason about causation and conditional independence. This work builds on recent work on Markov categories of probabilistic mappings to define a category whose morphisms combine a joint density, factorized over each sample space, with a deterministic mapping from samples to return values. This is a step towards closing the gap between recent category-theoretic descriptions of probability measures, and the operational definitions of factorized densities that are commonly employed in probabilistic programming and causal inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge