Data-efficient and Interpretable Inverse Materials Design using a Disentangled Variational Autoencoder

Inverse materials design has proven successful in accelerating novel material discovery. Many inverse materials design methods use unsupervised learning where a latent space is learned to offer a compact description of materials representations. A latent space learned this way is likely to be entangled, in terms of the target property and other properties of the materials. This makes the inverse design process ambiguous. Here, we present a semi-supervised learning approach based on a disentangled variational autoencoder to learn a probabilistic relationship between features, latent variables and target properties. This approach is data efficient because it combines all labelled and unlabelled data in a coherent manner, and it uses expert-informed prior distributions to improve model robustness even with limited labelled data. It is in essence interpretable, as the learnable target property is disentangled out of the other properties of the materials, and an extra layer of interpretability can be provided by a post-hoc analysis of the classification head of the model. We demonstrate this new approach on an experimental high-entropy alloy dataset with chemical compositions as input and single-phase formation as the single target property. While single property is used in this work, the disentangled model can be extended to customize for inverse design of materials with multiple target properties.

Analyzing the Effects of Classifier Lipschitzness on Explainers

Machine learning methods are getting increasingly better at making predictions, but at the same time they are also becoming more complicated and less transparent. As a result, explainers are often relied on to provide interpretability to these black-box prediction models. As crucial diagnostics tools, it is important that these explainers themselves are reliable. In this paper we focus on one particular aspect of reliability, namely that an explainer should give similar explanations for similar data inputs. We formalize this notion by introducing and defining explainer astuteness, analogous to astuteness of classifiers. Our formalism is inspired by the concept of probabilistic Lipschitzness, which captures the probability of local smoothness of a function. For a variety of explainers (e.g., SHAP, RISE, CXPlain), we provide lower bound guarantees on the astuteness of these explainers given the Lipschitzness of the prediction function. These theoretical results imply that locally smooth prediction functions lend themselves to locally robust explanations. We evaluate these results empirically on simulated as well as real datasets.

Deep Markov Spatio-Temporal Factorization

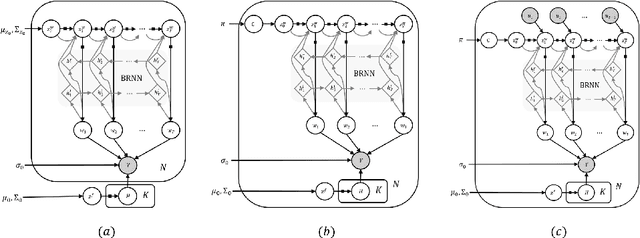
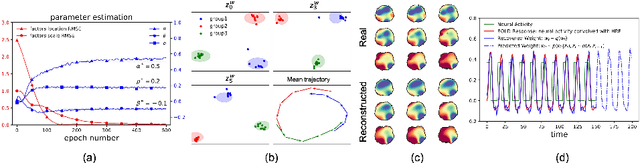
We introduce deep Markov spatio-temporal factorization (DMSTF), a deep generative model for spatio-temporal data. Like other factor analysis methods, DMSTF approximates high-dimensional data by a product between time-dependent weights and spatially dependent factors. These weights and factors are in turn represented in terms of lower-dimensional latent variables that we infer using stochastic variational inference. The innovation in DMSTF is that we parameterize weights in terms of a deep Markovian prior, which is able to characterize nonlinear temporal dynamics. We parameterize the corresponding variational distribution using a bidirectional recurrent network. This results in a flexible family of hierarchical deep generative factor analysis models that can be extended to perform time series clustering, or perform factor analysis in the presence of a control signal. Our experiments, which consider simulated data, fMRI data, and traffic data, demonstrate that DMSTF outperforms related methods in terms of reconstruction accuracy and can perform forecasting in a variety domains with nonlinear temporal transitions.

Deep Kernel Learning for Clustering

We propose a deep learning approach for discovering kernels tailored to identifying clusters over sample data. Our neural network produces sample embeddings that are motivated by--and are at least as expressive as--spectral clustering. Our training objective, based on the Hilbert Schmidt Information Criterion, can be optimized via gradient adaptations on the Stiefel manifold, leading to significant acceleration over spectral methods relying on eigendecompositions. Finally, our trained embedding can be directly applied to out-of-sample data. We show experimentally that our approach outperforms several state-of-the-art deep clustering methods, as well as traditional approaches such as $k$-means and spectral clustering over a broad array of real-life and synthetic datasets.

Neural Topographic Factor Analysis for fMRI Data

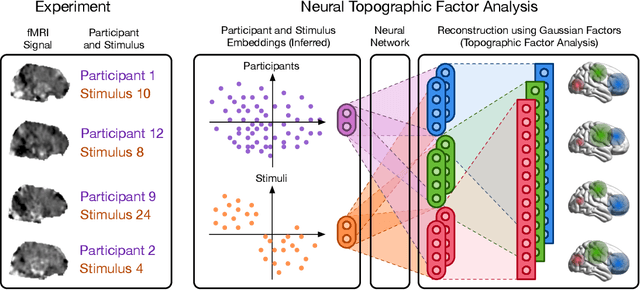
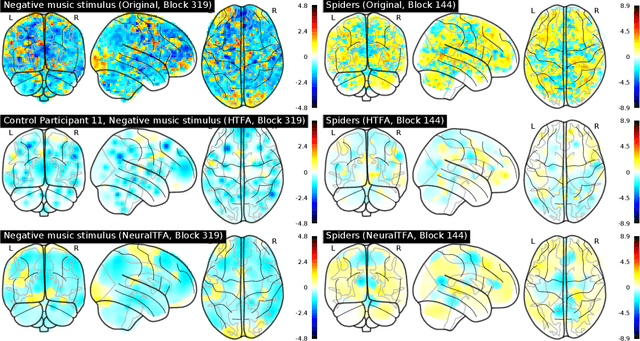
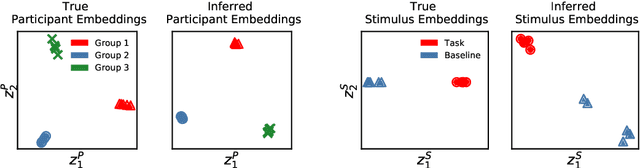
Neuroimaging experiments produce a large volume (gigabytes) of high-dimensional spatio-temporal data for a small number of sampled participants and stimuli. Analyses of this data commonly compute averages over all trials, ignoring variation within groups of participants and stimuli. To enable the analysis of fMRI data without this implicit assumption of uniformity, we propose Neural Topographic Factor Analysis (NTFA), a deep generative model that parameterizes factors as functions of embeddings for participants and stimuli. We evaluate NTFA on a synthetically generated dataset as well as on three datasets from fMRI experiments. Our results demonstrate that NTFA yields more accurate reconstructions than a state-of-the-art method with fewer parameters. Moreover, learned embeddings uncover latent categories of participants and stimuli, which suggests that NTFA takes a first step towards reasoning about individual variation in fMRI experiments.