Yale Chang
Convolution-Free Waveform Transformers for Multi-Lead ECG Classification
Sep 29, 2021



Abstract:We present our entry to the 2021 PhysioNet/CinC challenge - a waveform transformer model to detect cardiac abnormalities from ECG recordings. We compare the performance of the waveform transformer model on different ECG-lead subsets using approximately 88,000 ECG recordings from six datasets. In the official rankings, team prna ranked between 9 and 15 on 12, 6, 4, 3 and 2-lead sets respectively. Our waveform transformer model achieved an average challenge metric of 0.47 on the held-out test set across all ECG-lead subsets. Our combined performance across all leads placed us at rank 11 out of 39 officially ranking teams.
Interpretable Additive Recurrent Neural Networks For Multivariate Clinical Time Series
Sep 15, 2021Abstract:Time series models with recurrent neural networks (RNNs) can have high accuracy but are unfortunately difficult to interpret as a result of feature-interactions, temporal-interactions, and non-linear transformations. Interpretability is important in domains like healthcare where constructing models that provide insight into the relationships they have learned are required to validate and trust model predictions. We want accurate time series models where users can understand the contribution of individual input features. We present the Interpretable-RNN (I-RNN) that balances model complexity and accuracy by forcing the relationship between variables in the model to be additive. Interactions are restricted between hidden states of the RNN and additively combined at the final step. I-RNN specifically captures the unique characteristics of clinical time series, which are unevenly sampled in time, asynchronously acquired, and have missing data. Importantly, the hidden state activations represent feature coefficients that correlate with the prediction target and can be visualized as risk curves that capture the global relationship between individual input features and the outcome. We evaluate the I-RNN model on the Physionet 2012 Challenge dataset to predict in-hospital mortality, and on a real-world clinical decision support task: predicting hemodynamic interventions in the intensive care unit. I-RNN provides explanations in the form of global and local feature importances comparable to highly intelligible models like decision trees trained on hand-engineered features while significantly outperforming them. I-RNN remains intelligible while providing accuracy comparable to state-of-the-art decay-based and interpolation-based recurrent time series models. The experimental results on real-world clinical datasets refute the myth that there is a tradeoff between accuracy and interpretability.
Solving Interpretable Kernel Dimension Reduction
Sep 25, 2019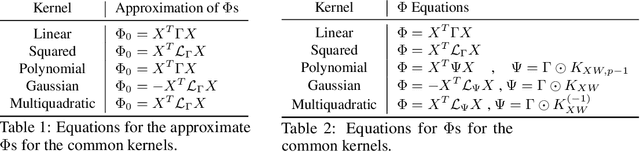



Abstract:Kernel dimensionality reduction (KDR) algorithms find a low dimensional representation of the original data by optimizing kernel dependency measures that are capable of capturing nonlinear relationships. The standard strategy is to first map the data into a high dimensional feature space using kernels prior to a projection onto a low dimensional space. While KDR methods can be easily solved by keeping the most dominant eigenvectors of the kernel matrix, its features are no longer easy to interpret. Alternatively, Interpretable KDR (IKDR) is different in that it projects onto a subspace \textit{before} the kernel feature mapping, therefore, the projection matrix can indicate how the original features linearly combine to form the new features. Unfortunately, the IKDR objective requires a non-convex manifold optimization that is difficult to solve and can no longer be solved by eigendecomposition. Recently, an efficient iterative spectral (eigendecomposition) method (ISM) has been proposed for this objective in the context of alternative clustering. However, ISM only provides theoretical guarantees for the Gaussian kernel. This greatly constrains ISM's usage since any kernel method using ISM is now limited to a single kernel. This work extends the theoretical guarantees of ISM to an entire family of kernels, thereby empowering ISM to solve any kernel method of the same objective. In identifying this family, we prove that each kernel within the family has a surrogate $\Phi$ matrix and the optimal projection is formed by its most dominant eigenvectors. With this extension, we establish how a wide range of IKDR applications across different learning paradigms can be solved by ISM. To support reproducible results, the source code is made publicly available on \url{https://github.com/chieh-neu/ISM_supervised_DR}.
Spectral Non-Convex Optimization for Dimension Reduction with Hilbert-Schmidt Independence Criterion
Sep 06, 2019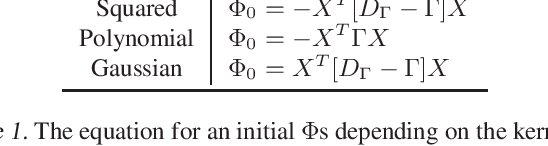


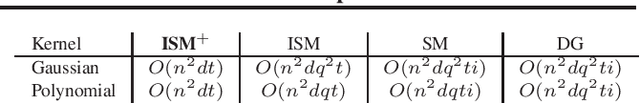
Abstract:The Hilbert Schmidt Independence Criterion (HSIC) is a kernel dependence measure that has applications in various aspects of machine learning. Conveniently, the objectives of different dimensionality reduction applications using HSIC often reduce to the same optimization problem. However, the nonconvexity of the objective function arising from non-linear kernels poses a serious challenge to optimization efficiency and limits the potential of HSIC-based formulations. As a result, only linear kernels have been computationally tractable in practice. This paper proposes a spectral-based optimization algorithm that extends beyond the linear kernel. The algorithm identifies a family of suitable kernels and provides the first and second-order local guarantees when a fixed point is reached. Furthermore, we propose a principled initialization strategy, thereby removing the need to repeat the algorithm at random initialization points. Compared to state-of-the-art optimization algorithms, our empirical results on real data show a run-time improvement by as much as a factor of $10^5$ while consistently achieving lower cost and classification/clustering errors. The implementation source code is publicly available on https://github.com/endsley.
Deep Kernel Learning for Clustering
Aug 09, 2019



Abstract:We propose a deep learning approach for discovering kernels tailored to identifying clusters over sample data. Our neural network produces sample embeddings that are motivated by--and are at least as expressive as--spectral clustering. Our training objective, based on the Hilbert Schmidt Information Criterion, can be optimized via gradient adaptations on the Stiefel manifold, leading to significant acceleration over spectral methods relying on eigendecompositions. Finally, our trained embedding can be directly applied to out-of-sample data. We show experimentally that our approach outperforms several state-of-the-art deep clustering methods, as well as traditional approaches such as $k$-means and spectral clustering over a broad array of real-life and synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge