SAIF: Sparse Adversarial and Interpretable Attack Framework

Adversarial attacks hamper the decision-making ability of neural networks by perturbing the input signal. The addition of calculated small distortion to images, for instance, can deceive a well-trained image classification network. In this work, we propose a novel attack technique called Sparse Adversarial and Interpretable Attack Framework (SAIF). Specifically, we design imperceptible attacks that contain low-magnitude perturbations at a small number of pixels and leverage these sparse attacks to reveal the vulnerability of classifiers. We use the Frank-Wolfe (conditional gradient) algorithm to simultaneously optimize the attack perturbations for bounded magnitude and sparsity with $O(1/\sqrt{T})$ convergence. Empirical results show that SAIF computes highly imperceptible and interpretable adversarial examples, and outperforms state-of-the-art sparse attack methods on the ImageNet dataset.

Solving Interpretable Kernel Dimension Reduction

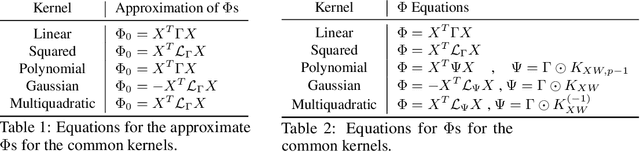
Kernel dimensionality reduction (KDR) algorithms find a low dimensional representation of the original data by optimizing kernel dependency measures that are capable of capturing nonlinear relationships. The standard strategy is to first map the data into a high dimensional feature space using kernels prior to a projection onto a low dimensional space. While KDR methods can be easily solved by keeping the most dominant eigenvectors of the kernel matrix, its features are no longer easy to interpret. Alternatively, Interpretable KDR (IKDR) is different in that it projects onto a subspace \textit{before} the kernel feature mapping, therefore, the projection matrix can indicate how the original features linearly combine to form the new features. Unfortunately, the IKDR objective requires a non-convex manifold optimization that is difficult to solve and can no longer be solved by eigendecomposition. Recently, an efficient iterative spectral (eigendecomposition) method (ISM) has been proposed for this objective in the context of alternative clustering. However, ISM only provides theoretical guarantees for the Gaussian kernel. This greatly constrains ISM's usage since any kernel method using ISM is now limited to a single kernel. This work extends the theoretical guarantees of ISM to an entire family of kernels, thereby empowering ISM to solve any kernel method of the same objective. In identifying this family, we prove that each kernel within the family has a surrogate $\Phi$ matrix and the optimal projection is formed by its most dominant eigenvectors. With this extension, we establish how a wide range of IKDR applications across different learning paradigms can be solved by ISM. To support reproducible results, the source code is made publicly available on \url{https://github.com/chieh-neu/ISM_supervised_DR}.

Spectral Non-Convex Optimization for Dimension Reduction with Hilbert-Schmidt Independence Criterion

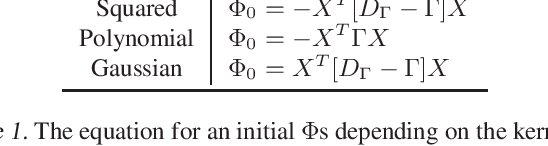
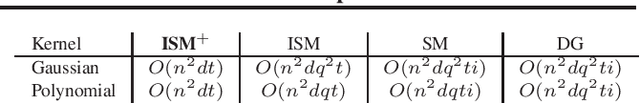
The Hilbert Schmidt Independence Criterion (HSIC) is a kernel dependence measure that has applications in various aspects of machine learning. Conveniently, the objectives of different dimensionality reduction applications using HSIC often reduce to the same optimization problem. However, the nonconvexity of the objective function arising from non-linear kernels poses a serious challenge to optimization efficiency and limits the potential of HSIC-based formulations. As a result, only linear kernels have been computationally tractable in practice. This paper proposes a spectral-based optimization algorithm that extends beyond the linear kernel. The algorithm identifies a family of suitable kernels and provides the first and second-order local guarantees when a fixed point is reached. Furthermore, we propose a principled initialization strategy, thereby removing the need to repeat the algorithm at random initialization points. Compared to state-of-the-art optimization algorithms, our empirical results on real data show a run-time improvement by as much as a factor of $10^5$ while consistently achieving lower cost and classification/clustering errors. The implementation source code is publicly available on https://github.com/endsley.