Deep Layer-wise Networks Have Closed-Form Weights

There is currently a debate within the neuroscience community over the likelihood of the brain performing backpropagation (BP). To better mimic the brain, training a network \textit{one layer at a time} with only a "single forward pass" has been proposed as an alternative to bypass BP; we refer to these networks as "layer-wise" networks. We continue the work on layer-wise networks by answering two outstanding questions. First, $\textit{do they have a closed-form solution?}$ Second, $\textit{how do we know when to stop adding more layers?}$ This work proves that the Kernel Mean Embedding is the closed-form weight that achieves the network global optimum while driving these networks to converge towards a highly desirable kernel for classification; we call it the $\textit{Neural Indicator Kernel}$.

Kernel Dependence Network

We propose a greedy strategy to spectrally train a deep network for multi-class classification. Each layer is defined as a composition of linear weights with the feature map of a Gaussian kernel acting as the activation function. At each layer, the linear weights are learned by maximizing the dependence between the layer output and the labels using the Hilbert Schmidt Independence Criterion (HSIC). By constraining the solution space on the Stiefel Manifold, we demonstrate how our network construct (Kernel Dependence Network or KNet) can be solved spectrally while leveraging the eigenvalues to automatically find the width and the depth of the network. We theoretically guarantee the existence of a solution for the global optimum while providing insight into our network's ability to generalize.

Layer-wise Learning of Kernel Dependence Networks

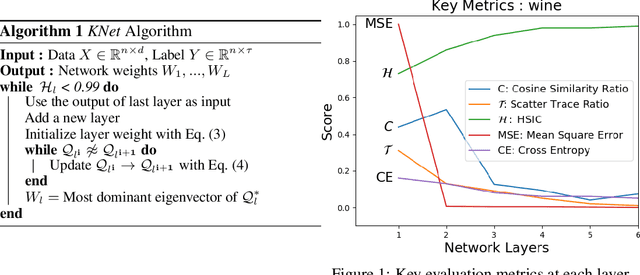
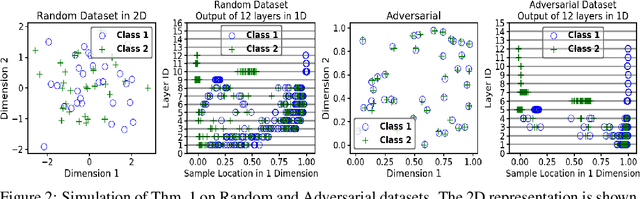
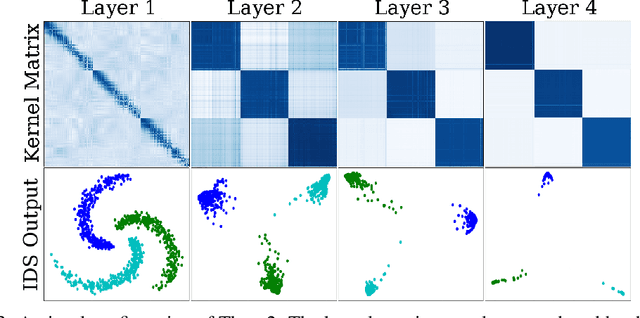
We propose a greedy strategy to train a deep network for multi-class classification, where each layer is defined as a composition of a linear projection and a nonlinear mapping. This nonlinear mapping is defined as the feature map of a Gaussian kernel, and the linear projection is learned by maximizing the dependence between the layer output and the labels, using the Hilbert Schmidt Independence Criterion (HSIC) as the dependence measure. Since each layer is trained greedily in sequence, all learning is local, and neither backpropagation nor even gradient descent is needed. The depth and width of the network are determined via natural guidelines, and the procedure regularizes its weights in the linear layer. As the key theoretical result, the function class represented by the network is proved to be sufficiently rich to learn any dataset labeling using a finite number of layers, in the sense of reaching minimum mean-squared error or cross-entropy, as long as no two data points with different labels coincide. Experiments demonstrate good generalization performance of the greedy approach across multiple benchmarks while showing a significant computational advantage against a multilayer perceptron of the same complexity trained globally by backpropagation.

Solving Interpretable Kernel Dimension Reduction

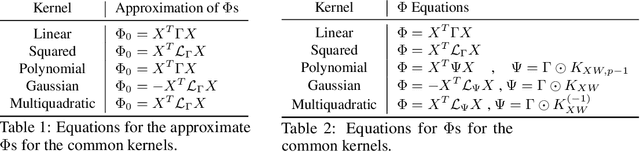
Kernel dimensionality reduction (KDR) algorithms find a low dimensional representation of the original data by optimizing kernel dependency measures that are capable of capturing nonlinear relationships. The standard strategy is to first map the data into a high dimensional feature space using kernels prior to a projection onto a low dimensional space. While KDR methods can be easily solved by keeping the most dominant eigenvectors of the kernel matrix, its features are no longer easy to interpret. Alternatively, Interpretable KDR (IKDR) is different in that it projects onto a subspace \textit{before} the kernel feature mapping, therefore, the projection matrix can indicate how the original features linearly combine to form the new features. Unfortunately, the IKDR objective requires a non-convex manifold optimization that is difficult to solve and can no longer be solved by eigendecomposition. Recently, an efficient iterative spectral (eigendecomposition) method (ISM) has been proposed for this objective in the context of alternative clustering. However, ISM only provides theoretical guarantees for the Gaussian kernel. This greatly constrains ISM's usage since any kernel method using ISM is now limited to a single kernel. This work extends the theoretical guarantees of ISM to an entire family of kernels, thereby empowering ISM to solve any kernel method of the same objective. In identifying this family, we prove that each kernel within the family has a surrogate $\Phi$ matrix and the optimal projection is formed by its most dominant eigenvectors. With this extension, we establish how a wide range of IKDR applications across different learning paradigms can be solved by ISM. To support reproducible results, the source code is made publicly available on \url{https://github.com/chieh-neu/ISM_supervised_DR}.

Iterative Spectral Method for Alternative Clustering

Given a dataset and an existing clustering as input, alternative clustering aims to find an alternative partition. One of the state-of-the-art approaches is Kernel Dimension Alternative Clustering (KDAC). We propose a novel Iterative Spectral Method (ISM) that greatly improves the scalability of KDAC. Our algorithm is intuitive, relies on easily implementable spectral decompositions, and comes with theoretical guarantees. Its computation time improves upon existing implementations of KDAC by as much as 5 orders of magnitude.

Spectral Non-Convex Optimization for Dimension Reduction with Hilbert-Schmidt Independence Criterion

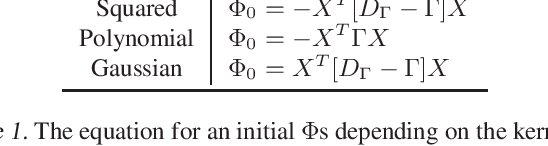
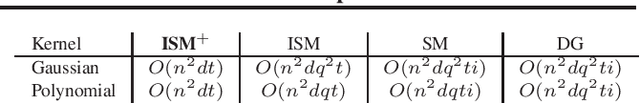
The Hilbert Schmidt Independence Criterion (HSIC) is a kernel dependence measure that has applications in various aspects of machine learning. Conveniently, the objectives of different dimensionality reduction applications using HSIC often reduce to the same optimization problem. However, the nonconvexity of the objective function arising from non-linear kernels poses a serious challenge to optimization efficiency and limits the potential of HSIC-based formulations. As a result, only linear kernels have been computationally tractable in practice. This paper proposes a spectral-based optimization algorithm that extends beyond the linear kernel. The algorithm identifies a family of suitable kernels and provides the first and second-order local guarantees when a fixed point is reached. Furthermore, we propose a principled initialization strategy, thereby removing the need to repeat the algorithm at random initialization points. Compared to state-of-the-art optimization algorithms, our empirical results on real data show a run-time improvement by as much as a factor of $10^5$ while consistently achieving lower cost and classification/clustering errors. The implementation source code is publicly available on https://github.com/endsley.

Deep Kernel Learning for Clustering

We propose a deep learning approach for discovering kernels tailored to identifying clusters over sample data. Our neural network produces sample embeddings that are motivated by--and are at least as expressive as--spectral clustering. Our training objective, based on the Hilbert Schmidt Information Criterion, can be optimized via gradient adaptations on the Stiefel manifold, leading to significant acceleration over spectral methods relying on eigendecompositions. Finally, our trained embedding can be directly applied to out-of-sample data. We show experimentally that our approach outperforms several state-of-the-art deep clustering methods, as well as traditional approaches such as $k$-means and spectral clustering over a broad array of real-life and synthetic datasets.